
- •1. Основные понятия теории графов, удаленность вершины, центр, радиус и диаметр графа.
- •2. Способы задания графов, свойства матриц смежности и инциденций, теорема о рукопожатиях.
- •3. Основные операции над графами, неравенства для числа вершин, ребер и компонент связности графа.
- •4. Типы графов, дополнительные графы, двудольные графы, критерий двудольности.
- •5. Обходы графов: эйлеровы цепи и циклы, необходимые и достаточные условия их существования, алгоритм Флери.
- •6. Обходы графов: гамильтоновы цепи и циклы, достаточные условия их существования.
- •7. Деревья, их свойства, кодирование деревьев, остовные деревья.
- •8. Экстремальные задачи теории графов: минимальное остовное дерево, алгоритмы Прима и Краскала.
- •9. Экстремальные задачи теории графов: задача коммивояжера, «жадный» алгоритм
- •10. Экстремальные задачи теории графов: задача о кратчайшем пути, алгоритм Дейкстры.
- •11. Изоморфизм и гомеоморфизм графов, методы доказательства изоморфности и неизоморфности графов.
- •12. Плоские укладки графов, планарные графы, критерий Понтрягина-Куратовского.
- •13. Необходимые условия планарности, формула Эйлера для планарных графов.
- •14. Правильные вершинные раскраски графов, хроматическое число, неравенства для хроматического числа.
- •15. Теорема о пяти красках, гипотеза четырех красок, «жадный» алгоритм.
- •16. Хроматический многочлен, его нахождение и свойства.
- •17. Задача о поиске выхода из лабиринта, реберная раскраска графа.
- •18. Ориентированные графы, источники и стоки, топологическая сортировка, алгоритм Демукрона.
- •19. Составление расписания выполнения комплекса работ в кратчайшие сроки методами теории графов.
- •20. Элементарные булевы функции и способы их задания (табличный, векторный, формульный, графический, карта Карно).
- •21. Существенные и фиктивные переменные булевых функций, основные тождества, эквивалентные преобразования формул.
- •22. Линейные и нелинейные полиномы Жегалкина, разложение булевых функций в полином Жегалкина методом неопределенных коэффициентов.
- •23. Линейные и нелинейные полиномы Жегалкина, разложение булевых функций в полином Жегалкина методом эквивалентных преобразований.
- •24. Разложение булевых функций в сднф и скнф.
- •25. Минимизация днф и кнф методом эквивалентных преобразований.
- •26. Минимизация днф и кнф с помощью карт Карно.
- •27. Замкнутые классы булевых функций т0, т1, l, лемма о нелинейной функции.
- •28. Замкнутые классы булевых функций s и м, леммы о несамодвойственной и немонотонной функции.
- •29. Полная система функций, теорема о двух системах булевых функций.
- •30. Теорема Поста о полноте системы булевых функций, алгоритм проверки системы на полноту, базис.
- •31. Схемы из функциональных элементов, правила построения и функционирования, метод синтеза сфэ, основанный на сднф и скнф.
- •32. Метод синтеза сфэ, основанный на компактной реализации всех конъюнкций с помощью универсального многополюсника, сложность получаемых схем.
- •33. Основные комбинаторные операции, сочетания и размещения (с возвращением и без возвращения элементов).
- •34. Комбинаторные принципы сложения, умножения, дополнения, включения-исключения.
- •35. Биномиальные коэффициенты, их свойства, бином Ньютона.
- •36. Треугольник Паскаля, полиномиальная формула.
- •37. Алфавитное кодирование: необходимое и достаточные условия однозначности декодирования.
- •38. Алфавитное кодирование: теорема Маркова, алгоритм Маркова.
- •39. Коды с минимальной избыточностью (коды Хаффмана), метод построения.
- •40. Линейные коды, порождающая матрица, двойственный код.
- •41. Самокорректирующиеся коды (коды Хэмминга), метод построения.
- •42. Определение, схема и функционирование абстрактного автомата, способы задания автоматов.
- •43. Типы конечных автоматов, автоматы Мили и Мура, автоматы-генераторы.
- •44. Слова и языки, операции над ними, их свойства.
- •45. Регулярные выражения и регулярные языки, теорема Клини.
- •46. Задача анализа автоматов-распознавателей.
- •47. Задача синтеза автоматов-распознавателей.
- •48. Эквивалентные состояния автомата-распознавателя, эквивалентные автоматы-распознаватели, минимизация автоматов-распознавателей, алгоритм Мили.
- •49. Эквивалентные состояния автомата-преобразователя, эквивалентные автоматы- преобразователи, минимизация автоматов- преобразователей, алгоритм Мили.
- •50. Детерминированные и недетерминированные функции, примеры, способы задания.
- •51. Ограниченно-детерминированные (автоматные) функции, способы их задания.
- •52. Логические автоматы, способы их задания, синтез двоичного сумматора.
- •53. Операции над логическими автоматами: суперпозиция и введение обратной связи.
33. Основные комбинаторные операции, сочетания и размещения (с возвращением и без возвращения элементов).
Определение. Выборка – это простейшая комбинаторная операция, применяемая к заданному множеству и состоящая в том, что из этого множества выбирается произвольный элемент. Если выбранный элемент удаляют из исходного множества, то такую операцию называют выборкой без возвращения. Если же элемент остается в исходном множестве, то такая выборка называется выборкой с возвращением.
Определение. Повторная выборка k элементов из n-элементного множества без возвращения и без упорядочения называется сочетанием из n по k.
Определение. Повторная выборка k элементов из n-элементного множества без возвращения, но с упорядочением, называется размещением из n по k.
Утверждение.
Число различных сочетаний из n
по
k
обозначается через
 ,
, .
.
Утверждение.
Число различных размещений из n
по
k
обозначается через
 ,
,
Утверждение.
Число различных размещений с повторениями
 изn
элементов по k,
где k
= 0, 1, 2,…, равно
изn
элементов по k,
где k
= 0, 1, 2,…, равно
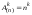 .
.
Утверждение.
Число различных сочетаний с повторениями
 изn
элементов по k,
где k=0,1,2,…,
равно
изn
элементов по k,
где k=0,1,2,…,
равно
 .
.
|
Выборки из nпоk |
Без возвращения (0 ≤ k ≤ n) |
С возвращением |
|
С упорядочением |
Размещения
|
Размещения с повторениями
|
|
Без упорядочения |
Сочетания
|
Сочетания с повторениями
|
34. Комбинаторные принципы сложения, умножения, дополнения, включения-исключения.
Комбинаторный
принцип сложения.Суть этого
метода в следующем: пусть требуется
вычислить количество элементов в
некотором множестве В. Если данное
множество можно разбить на несколько
непересекающихся подмножеств В1,
В2, …, Вmи
найти их мощности, то число элементов
во множестве В можно получить сложением
мощностей подмножеств В1, В2,
…, Вm, т.е. .
.
Комбинаторный
принцип умножения.
Пусть |A| = p,
|B| = q,
тогда существует ровно
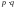 различных пар, в которых первый элемент
взят из множества А, а второй элемент –
из множества В.
различных пар, в которых первый элемент
взят из множества А, а второй элемент –
из множества В.
Комбинаторный
принцип включения – исключенияявляется обобщением принципа сложения.
Он применяется даже тогда, когда принцип
сложения не работает, а именно, если
исходное множество является объединением
двух и более пересекающихся подмножеств.
В самом простом виде принцип
включения – исключения основывается
на очевидном соотношении .
Также имеет место равенство:
.
Также имеет место равенство:
35. Биномиальные коэффициенты, их свойства, бином Ньютона.
Комбинаторные
числа сочетаний
 ,
гдеk = 0,1,2,…,nназывают биномиальными
коэффициентами, поскольку они связаны
с биномом Ньютона (x+y)n.
Для любого натуральногоnвыполняется равенство:
,
гдеk = 0,1,2,…,nназывают биномиальными
коэффициентами, поскольку они связаны
с биномом Ньютона (x+y)n.
Для любого натуральногоnвыполняется равенство:

 .
.
Пример. Требуется вычислить коэффициент при а9после раскрытия скобок в выражении (4а – 5)11.
В
формуле положим
 .
Тогда получим
.
Тогда получим .
Интересующее нас слагаемое, содержащее
а9, получается приk= 2 и имеет вид
.
Интересующее нас слагаемое, содержащее
а9, получается приk= 2 и имеет вид .
Отсюда следует, что искомый коэффициент
равен
.
Отсюда следует, что искомый коэффициент
равен .
.
Биномиальные коэффициенты обладают многими свойствами, среди которых наиболее важными являются следующие:
 ,
,
 ,
,
 ,
,
 .
.
36. Треугольник Паскаля, полиномиальная формула.
Комбинаторные
числа сочетаний
 ,
гдеk = 0,1,2,…,nназывают биномиальными
коэффициентами, поскольку они связаны
с биномом Ньютона (x+y)n.
Для любого натуральногоnвыполняется равенство:
,
гдеk = 0,1,2,…,nназывают биномиальными
коэффициентами, поскольку они связаны
с биномом Ньютона (x+y)n.
Для любого натуральногоnвыполняется равенство:

 .
.
Треугольник Паскаля.
На
основе свойства
 из биномиальных коэффициентов построен
треугольник Паскаля.
из биномиальных коэффициентов построен
треугольник Паскаля.
Этот
треугольник состоит из бесконечного
числа горизонтальных рядов, которые
для удобства будем нумеровать числами
n= 0, 1, 2, 3 и
т.д., а элементы каждого ряда - слева
направо числамиk= 0, 1, 2, …,n.
Тогда правило построения этого
треугольника Паскаля можно сформулировать
так: начальный и конечный элементы
каждого ряда равны 1, аk-й
элементn-го ряда приk= 1, 2, …,n– 1
и приn= 2, 3, 4 и
т.д. равен сумме (k– 1)-го
иk-го элемента (n– 1)-го
ряда. Тогда согласно свойству ,
еслиk= 0, 1, 2, …,n,
аn= 0, 1, 2, 3
и т.д., тоk-й элементn-го
ряда равен
,
еслиk= 0, 1, 2, …,n,
аn= 0, 1, 2, 3
и т.д., тоk-й элементn-го
ряда равен .
Из формулы
.
Из формулы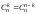 вытекает свойство симметричности
треугольника Паскаля относительно
вертикальной прямой, проходящей через
его вершину. Эта симметричность выражается
в том, что совпадают элементы, стоящие
в одном ряду на одинаковом расстоянии
от концов ряда. Из формулы
вытекает свойство симметричности
треугольника Паскаля относительно
вертикальной прямой, проходящей через
его вершину. Эта симметричность выражается
в том, что совпадают элементы, стоящие
в одном ряду на одинаковом расстоянии
от концов ряда. Из формулы следует,
что сумма всех элементовn-го
ряда равна 2n,
а из
следует,
что сумма всех элементовn-го
ряда равна 2n,
а из получается, что в каждом ряду суммы
элементов, стоящих на четных и нечетных
местах, равны между собой.
получается, что в каждом ряду суммы
элементов, стоящих на четных и нечетных
местах, равны между собой.
Полиномиальная формула.
Обобщением биномиальной формулы является полиномиальная формула

 .
.
Каждый
числовой коэффициент
 называется полиномиальным коэффициентом.
Он равен числу различных вариантов
упорядоченного разбиенияn-элементного
множества наkнепересекающихся
подмножеств мощностиn1,n2,n3,…,nk.
Приk= 2 равенство обращается
в формулу для бинома Ньютона.
называется полиномиальным коэффициентом.
Он равен числу различных вариантов
упорядоченного разбиенияn-элементного
множества наkнепересекающихся
подмножеств мощностиn1,n2,n3,…,nk.
Приk= 2 равенство обращается
в формулу для бинома Ньютона.
Пример. Требуется вычислить коэффициент при с17после раскрытия скобок в выражении (1+2с – с3)10.
После
раскрытия скобок в выражении (1+2с −
с3)10получится различных слагаемых, причем максимальный
показатель степени переменной с будет
равен 30. В формуле (40) положим х1=
1, х2= 2с, х3 = − с3,n= 10. Получим равенство
различных слагаемых, причем максимальный
показатель степени переменной с будет
равен 30. В формуле (40) положим х1=
1, х2= 2с, х3 = − с3,n= 10. Получим равенство ,
где суммирование в правой части ведется
по всем наборам целых неотрицательных
чисел (n1,n2,n 3) таких, чтоn1+n2
+n 3 =
10. Очевидно, что каждое слагаемое в
правой части содержит множитель вида
,
где суммирование в правой части ведется
по всем наборам целых неотрицательных
чисел (n1,n2,n 3) таких, чтоn1+n2
+n 3 =
10. Очевидно, что каждое слагаемое в
правой части содержит множитель вида .
Поскольку нас интересует коэффициент
при с17, то необходимо рассмотреть
все целочисленные неотрицательные
решения уравненияn2 + 3n3 = 17,
удовлетворяющие дополнительному условию
.
Поскольку нас интересует коэффициент
при с17, то необходимо рассмотреть
все целочисленные неотрицательные
решения уравненияn2 + 3n3 = 17,
удовлетворяющие дополнительному условию .
Таких решений всего два:n2 = 2,n3 = 5 иn2 = 5,n3 = 4.
Соответствующие значенияn1 =
3 иn1 = 1, а
числовые коэффициенты при с17будут равны соответственно
.
Таких решений всего два:n2 = 2,n3 = 5 иn2 = 5,n3 = 4.
Соответствующие значенияn1 =
3 иn1 = 1, а
числовые коэффициенты при с17будут равны соответственно и
и .
Следовательно, искомый коэффициент
равен 40320 – 10080 = 30240.
.
Следовательно, искомый коэффициент
равен 40320 – 10080 = 30240.




