
сопромат2
.pdfФедеральное агентство по образованию РФ Пермский государственный технический университет Кафедра конструирования машин и сопротивления материалов
СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ
Учебное пособие и задания по сопротивлению материалов для студентов
заочного отделения строительных специальностей
Часть ІІ
Пермь 2009
Составители: В.Е. Калугин, Т.Э. Римм, Ю.П. Сметанников
УДК 620.10
Сопротивление материалов. Учебное пособие и задания по сопротивлению материалов для студентов заочного отделения строительных специальностей. Часть ІІ. /
Составители: В.Е. Калугин, Т.Э. Римм, Ю.П. Сметанников. Пермский государственный технический университет. Пермь, 2009.
Рецензент: профессор Н.Н. Вассерман.
© Пермский государственный технический университет, 2009 г.
СОДЕРЖАНИЕ |
|
Глава VII. Статически неопределимые стержневые системы.................. |
5 |
7.1 Понятие о степени статической неопределимости, основной и |
|
эквивалентной стержневых системах. Канонические уравнения метода |
|
сил........................................................................................................................ |
5 |
7.2.Пример расчета статически неопределимой балки............................... |
8 |
7.3.Пример расчета статически неопределимой рамы.............................. |
14 |
7.4. Использование свойств симметрии стержневой системы и |
|
нагрузки при решении статически неопределимых систем........................... |
17 |
7.5. Пример расчета симметричной статически неопределимой |
|
рамы, загруженной кососимметричной нагрузкой (рис.7.38)........................ |
20 |
7.6. Контрольные задания № 13, 14 .......................................................... |
23 |
Глава VIII. Основы теории напряженного и деформированного |
|
состояния в точке. Теории прочности......................................................... |
27 |
8.1 Напряженное состояние в точке........................................................... |
27 |
8.2. Закон парности касательных напряжений .......................................... |
28 |
8.3. Главные площадки и главные напряжения. Виды напряжённого |
|
состояния........................................................................................................... |
29 |
8.4. Линейное напряжённое состояние ...................................................... |
30 |
8.5. Плоское напряжённое состояние ........................................................ |
30 |
8.6. Определение величины и направления главных напряжений........... |
31 |
8.7. Максимальные касательные напряжения ........................................... |
33 |
8.8. Объёмное напряжённое состояние...................................................... |
33 |
8.8.1. Обобщённый закон Гука................................................................... |
33 |
8.8.2. Относительное изменение объёма ................................................... |
35 |
8.8.3. Удельная потенциальная энергия..................................................... |
37 |
8.8.4. Потенциальная энергия изменения объёма и формы...................... |
37 |
8.9. Понятие о теории предельного состояния.......................................... |
38 |
8.10. Критерии разрушения ........................................................................ |
41 |
8.11. Критерии пластичности ..................................................................... |
42 |
8.12. Пример анализа плоского напряжённого состояния в точке |
|
тела .................................................................................................................... |
46 |
8.13. Контрольное задание № 15................................................................ |
50 |
3 |
|
Глава IX. Сложное сопротивление.............................................................. |
52 |
9.1. Общие понятия..................................................................................... |
52 |
9.2. Косой изгиб .......................................................................................... |
53 |
9.3. Изгиб с растяжением (сжатием).......................................................... |
56 |
9.3.1 Косой изгиб с растяжением (сжатием) ............................................. |
56 |
9.3.2. Внецентренное растяжение (сжатие) стержня большой |
|
жесткости .......................................................................................................... |
58 |
9.4. Изгиб с кручением ............................................................................... |
60 |
9.4.1. Изгиб с кручением круглых валов ................................................... |
61 |
9.5. Пример расчета стержня массивного сечения на внецентренное |
|
сжатие................................................................................................................ |
63 |
9.6. Пример расчета ломаного стержня на прочность при изгибе с |
|
кручением.......................................................................................................... |
66 |
9.7. Контрольные задачи............................................................................. |
68 |
9.7.1. Контрольно задание № 16. Расчет стержня массивного сечения |
|
на внецентренное сжатие. ................................................................................ |
68 |
9.7.2. Контрольное задание № 17. Расчет ломаного стержня на |
|
прочность при изгибе с кручением.................................................................. |
70 |
Глава X. Устойчивость сжатых стержней.................................................. |
72 |
10.1. Основные понятия.............................................................................. |
72 |
10.2. Практический расчет сжатых стержней............................................ |
75 |
10.3.Примеры расчета центрально сжатых стержней на
устойчивость..................................................................................................... |
76 |
Пример 1...................................................................................................... |
76 |
Пример 2...................................................................................................... |
79 |
10.4. Контрольное задание №18................................................................. |
82 |
Глава ХI. Техническая теория удара .......................................................... |
84 |
11.1. Упрощающие гипотезы теории удара............................................... |
84 |
11.2. Удар по безмассовой упругой системе ............................................. |
85 |
11.3. Удар по системе с промежуточной массой m1.................................. |
87 |
11.4. Пример расчета рамы на прочность при ударе................................. |
89 |
11.5. Контрольное задание 19. Расчет рамы на прочность и |
|
жесткость при ударе ......................................................................................... |
93 |
Список литературы ....................................................................................... |
93 |
4
Глава VII. Статически неопределимые стержневые системы
7.1 Понятие о степени статической неопределимости, основной и эквивалентной стержневых системах. Канонические уравнения метода сил.
Статически неопределимой стержневой системой называется система, у
которой опорные реакции и внутренние силовые факторы не могут быть найдены из одних лишь уравнений равновесия. Статически неопределимая система характеризуется степенью статической неопределимости. Степень статической неопределимости равна числу избыточных внешних или внутренних связей,
наложенных на систему. Избыточными называются такие связи, которые можно устранить, не нарушая геометрическую и мгновенную неизменяемость системы, т.е. не превращая систему в механизм и не
P P
Рис.7.1 |
Рис.7.2 |
вызывая изменение положения системы. |
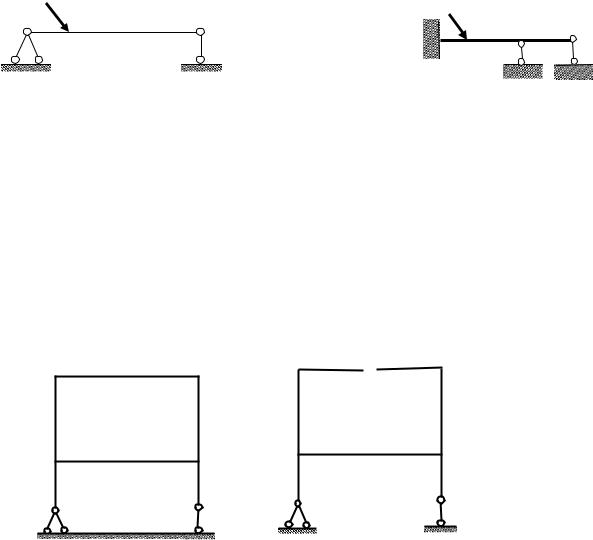
Так у двухопорной балки (рис.7.1) |
все три наложенные связи необходимые. |
Устранение любой связи нарушит |
геометрическую неизменяемость балки (балка будет вращаться, если убрать правую вертикальную связь, перемещаться в горизонтальном направлении, если убрать горизонтальную связь, потеряет мгновенную неизменяемость системы, если убрать левую вертикальную связь). Следовательно, балка статически определима. У балки на рис.7.2 можно устранить две связи (рис.7.6 и 7.7), не нарушая её геометрическую неизменяемость, поэтому степень статической неопределимости балки равна двум.
Избыточными могут быть не только опорные или внешние связи, но
P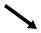
1
2 |
|
3 |
|
Рис.7.3 |
Рис.7.4 |
|
внутренние. Так на рис.7.3 реакции опор рамы можно определить из уравнений равновесия, однако внутренние усилия в стержнях, образующих верхний замкнутый контур, определить невозможно. Чтобы превратить раму в статически определимую, необходимо замкнутый контур разрезать в любом сечении. При
5
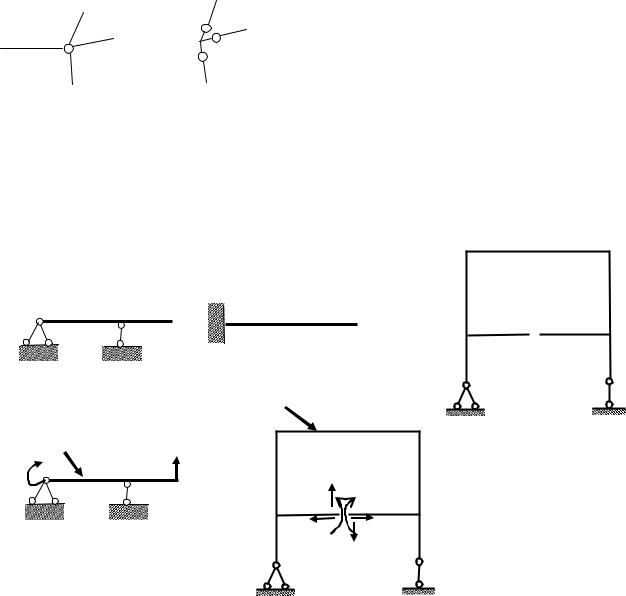
этом освобождается три внутренних связи – связь, препятствующая взаимному повороту сечений, связи, ограничивающие взаимное горизонтальное и вертикальное перемещения сечений в месте рассечения (рис.7.4). Таким образом, замкнутый жесткий контур трижды статически неопределим. Отметим, что врезание в замкнутый контур шарнира освобождает одну внутреннюю связь, а врезание шарнира в узел, соединяющий n стержней, освобождает n-1 внутренних связей, препятствующих взаимному повороту стержней друг относительно друга. К примеру, на рис.7.5 показано, что один групповой шарнир, соединяющий четыре стержня, эквивалентен трем одиночным шарнирам. С учетом вышеизложенного, степень статической неопределимости плоской стержневой системы можно определить по формуле:
|
|
S = 3K − Ш, |
|
|
|
|
|
|
|
|
|
где К − число замкнутых контуров, |
|
|
|||||
= |
|
Ш − число |
шарниров |
в |
пересчете |
на |
|||
|
одиночные. |
|
|
K = 2, |
|
Ш = 4, |
|||
|
|
|
|
|
|||||
|
|
Для балки на рис.7.2 |
а |
||||||
|
|
следовательно |
S = 3× 2 - 4 = 2. |
Для |
рамы |
на |
|||
Рис.7.5 |
|
рис.7.3 K = 3, Ш = 6, |
S = 3× 3 - 6 = 3. |
Рама |
|||||
состоит из трех контуров: контура образованного стержнями и «землей» (контур 2), контура образованного только стержнями (контур 1) и контура ограниченного опорными стержнями и «землей» (контур 3). Шарнир, соединяющий три стержня на неподвижной опоре двойной.
|
Рис.7.6 |
Рис.7.7 |
|
|
|
|
|
|
|
P |
Рис.7.8 |
|
|
|
|
X1 |
P |
X 2 |
|
|
|
X 2 |
X 3 |
|
Рис.7.9 |
X1 |
X1 |
|
|
X 2 |
|
|
|
Рис.7.10 |
|
|
Cтержневая система, полученная из исходной после устранения |
||
избыточных связей, называется основной. |
|||
6

Так как убирать можно различные связи, то для каждой исходной системы можно получить множество вариантов основных. На рис.7.6 и 7.7 приведены два варианта основных систем для исходной балки рис.7.2, а на рис.7.4 и 7.8 два варианта основных систем для рамы рис.7.3.
Таким образом, основная система должна быть статически определимой, кинематически неизменяемой, а при её выборе избыточные связи можно только отбрасывать, не добавляя новых.
Если к основной системе приложить внешние силы, а действие отброшенных связей заменить их реакциями, то получим эквивалентную систему (рис.7.9 и 7.10). Условие эквивалентности исходной системы, к примеру, рамы (рис.7.3) и ей эквивалентной (рис.7.10) послужит равенство нулю взаимных линейных и угловых перемещений в сечении, где связи отброшены:
1( X1, X2 , X3, ,P) 2( X1 ,X2 ,X3 ,P) 3( X1,X 2 ,X3 ,P)
= 0
= 0 |
(7.1) |
= 0 |
|
где i( X1, X 2 , X3 ,P) − перемещение в направлении i − той связи от внешних сил
и реакций отброшенных связей. Если удовлетворить условие (8.1), то в эквивалентной системе будут такие же деформации и напряжения, что и в исходной.
На основании принципа независимости действия сил условие (8.1) можно записать следующим образом:
|
|
1X1 + 1X 2 + 1X3 + 1P = 0 |
|
|
|
|
|
||||
|
|
2 X1 + 2 X2 + |
2 X3 |
+ |
2P |
= 0 |
|
|
|
|
(7.2) |
|
|
3 X1 + 3 X2 + 3X3 + 3P = 0 |
|
|
|
|
|
||||
где |
iX j |
−перемещение в направлении i-й отброшенной связи от реакции X j , |
|||||||||
|
iP |
− перемещение |
в |
направлении |
i-й |
отброшенной |
связи |
от |
внешней |
||
нагрузки. |
|
|
|
|
|
|
|
|
|
||
|
Так как перемещения пропорциональны силам (закон Гука), то условие (7.2) |
||||||||||
можно представить в виде: |
|
|
|
|
|
|
|
||||
|
δ11 X1 + δ12 X 2 + δ13 X 3 + 1P = 0 |
|
|
|
|
|
|||||
|
δ21 X1 + δ22 X 2 |
+ δ23 X 3 |
+ |
2 P = 0 |
|
|
|
|
(7.3) |
||
|
δ31 X1 + δ32 X 2 + δ33 X 3 + 3P = 0 |
|
|
|
|
|
|||||
гдеδij |
− коэффициент |
пропорциональности, |
физический |
смысл |
которого |
||||||
определяется исходя из равенства iX j = δij X j |
при X j = 1. В этом случае |
iX j = δij , |
|||||||||
т.е. δij это перемещение в направлении Xi |
от силы равной единице, приложенной |
||||||||||
вместо |
X j . Система уравнений (7.3) относительно неизвестных |
X j называется |
|||||||||
каноническими уравнениями метода сил. Их число всегда равно числу
неизвестных |
X j и записываются они |
всегда |
по |
одному и тому же правилу |
||
(канону). Коэффициенты δij |
и свободные члены |
iP |
суть перемещения, поэтому |
|||
могут быть |
определены |
интегралом |
Мора |
или |
способом Верещагина. В |
|
7

результате решения системы (7.3) получаем X j , которые на эквивалентной
системе рассматриваются в совокупности с заданной нагрузкой как внешние силы. Далее все необходимые расчеты (на прочность, жесткость и т.д.) проводятся для эквивалентной системы по методике, используемой для статически определимых систем, поскольку эквивалентная система статически определима, а напряжения и деформации в ней такие же, что и в исходной статически неопределимой системе.
Обобщая рассмотренную форму записи канонических уравнений, покажем, как записываются n уравнений для n раз статически неопределимой стержневой
системы: |
|
|
|
|
|
|
δ11 X1 |
+ δ12 X 2 |
+ ...+ δ1n X n |
+ |
1P |
= 0 |
|
δ21 X1 |
+ δ22 X 2 |
+ ...+ δ2n X n |
+ |
2P |
= 0 |
|
…………………………………… |
(7.4) |
|||||
…………………………………… |
|
|||||
δn1 X1 |
+ δn2 X 2 |
+ ...+ δnn X n |
+ |
nP |
= 0 |
|
Итак, каждое из канонических уравнений (7.4) |
– условие равенства нулю |
|||||
линейных и угловых перемещений в основной системе по направлению реакций в отброшенных связях. Величины δij (i, j = 1,2,...,n ) называются коэффициентами
системы (7.4), а iP - грузовыми или свободными членами. Отметим, что δij =δ ji -
взаимные единичные перемещения равны. В этом легко убедиться на примере, который рассмотрим, чтобы познакомиться с порядком решения статически неопределимых систем.
7.2.Пример расчета статически неопределимой балки.
Для балки, изображенной на рис.7.11, раскрыть статическую неопределимость, подобрать из условия прочности двутавровое сечение неразрезной стальной балки, если R=210МПа, определить перемещение сечения А левой консоли и угол поворота на одной из опор.
P = 10кН |
|
q=20кН/м |
M |
0 = 20кНм |
||||
|
|
|
||||||
|
|
|
|
|
|
|||
A |
|
B |
|
|
D |
|
||
|
2м |
|
|
2м |
|
C 1м |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
Рис.7.11
1. Определяем степень статической неопределимости.
S = 3K - Ш = 3× 2 - 4 = 2.
8
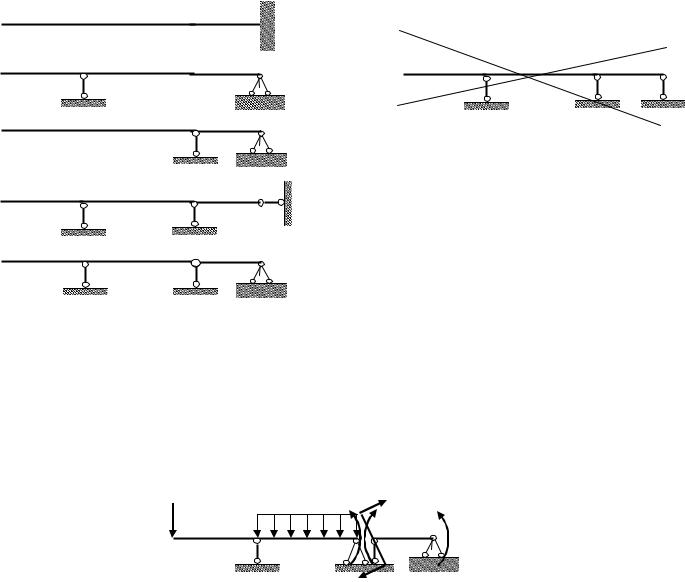
2. Для заданной балки изображаем несколько основных систем, одну из которых принимаем для расчета (рис.7.12). Отметим, что основная система на рис.8.12 f) выбрана неправильно, хотя отброшено, как и в предыдущих случаях, две связи. Под действием сил возможно перемещение этой балки в горизонтальном направлении, т.е. балка превратится в механизм.
Для дальнейшего решения выбираем основную систему с врезными шарнирами на промежуточной опоре и в защемлении (рис. 7.12е), так как в этом
случае определение коэффициентов канонических уравнений несколько упрощается. Во врезных идеальных шарнирах изгибающие моменты равны нулю, т. е. многопролетная балка превращается в отдельные статически определимые балки АС, и СD (рис.7.12е), эпюры изгибающих моментов в которых, при наличии определенного навыка, можно построить не прибегая к определению реакций опор.
a)
b) |
f) |
c) |
|
d) |
|
|
|
|
|
|
e) |
A |
C |
D |
|
|
|
|
Рис.7.12 |
|
|
|
|
|
|
3. Изображаем эквивалентную систему (см. рис.7.13) и записываем |
|||||
|
канонические уравнения метода сил: |
|
|
|
||
|
|
|
δ11Х1+δ12Х2+ 1р=0, |
|
||
|
|
|
δ21Х1+δ22Х2+ |
2р=0. |
|
|
|
P = 10кН |
q=20кН/м X1 |
|
|
||
|
|
В |
|
|
||
|
А |
|
С |
D |
X2 |
|
|
|
2м |
2м |
1м |
|
|
|
|
|
Рис.7.13 |
M 0 = 20КНм |
||
|
|
|
|
|
||
9
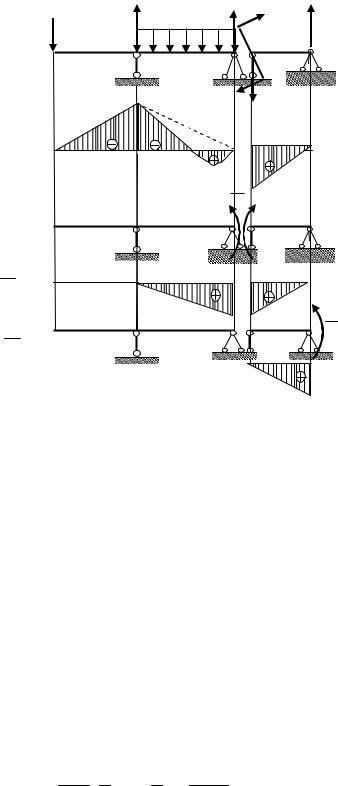
Первое уравнение – условие равенства нулю взаимного угла поворота поперечных сечений, примыкающих к сечению С, второе – условие равенства
P = 10кН R1=40kH R2=10 kH R4=20kH
q=20кН/м
а) |
M P |
|
(кНм) |
||
|
b)M 1
c)M 2
2м |
2м |
|
1м |
|
|
20 |
M 0 = 20кНм |
|
|
||
|
R3=20 kH |
|
|
||
|
20 |
= 1 |
|
|
|
|
X 1 |
|
|
|
|
|
1 |
1 |
X 2 |
= 1 |
|
|
|
|
|
||
|
Рис.7.14 |
|
|
1 |
|
нулю угла поворота поперечного сечения D.
4.Строим эпюры изгибающих моментов в основной системе от заданных нагрузок (рис.7.14а) и единичных силовых факторов (рис. 7.14в и 7.14с).
5.Вычисляем коэффициенты и свободные члены канонических уравнений по способу Верещагина.
D1P |
= |
|
1 |
|
(- |
|
1 |
20 × 2 × |
1 |
|
+ |
20 ×8 |
× |
1 |
+ |
1 |
20 ×1× |
1 |
) = |
20 |
; |
|||||||||||||||||||||||
|
EJ x |
2 |
3 |
|
|
|
|
|
|
|
|
|
3 |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 2 2 |
|
|
|
3EJ x |
||||||||||||||||||||
D2 P |
= |
1 |
|
|
( |
1 |
|
20×1× |
1 |
) = |
10 |
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
EJ x |
2 |
|
|
|
|
|
|
3 |
|
|
|
|
|
3EJ x |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
δ12 |
= δ21 = |
1 |
|
|
( |
1 |
|
×1×1× |
1 |
) = |
1 |
|
; |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
EJ x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
3 |
|
6EJ x |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
δ11 |
= |
|
1 |
( |
|
1 |
×1× 2 × |
|
2 |
+ |
|
1 |
×1×1× |
2 |
) = |
|
|
1 |
; |
|
|
|
|
|||||||||||||||||||||
|
|
2 |
3 |
2 |
3 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
EJ x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
EJ x |
|
|
|
|
|
|
||||||||||||
δ22 = EJ1 x (12 ×1×1× 23) = 3EJ1 x .
Врезультате подстановки значений коэффициентов и свободных членов в
канонические уравнения получаем систему относительно неизвестных X1 и X2:
10
