Лекция 2

Ускорение точки. Кинематика твёрдого тела. Поступательное и вращательное движения твердого тела.

Вопросы лекции.

1. Ускорение точки.

2. Общие понятия кинематики тела.

3. Поступательное движение тела.

4. Вращательное движение тела.

Скорость точки

Скорость точки характеризует «быстроту» изменения её положения. Формально: скорость – перемещение точки за единицу времени.

Точное определение.

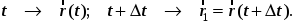
Тогда 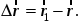Отношение

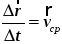11\* MERGEFORMAT ()

называется средней скоростью за промежуток времени t.

Переходя в (9) к пределу при 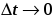получим

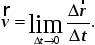22\* MERGEFORMAT ()

получим мгновенную скорость точки, или скорость точки в данный момент, или скорость точки.

Так как

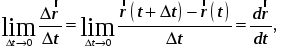
то, окончательно,

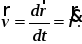33\* MERGEFORMAT ()

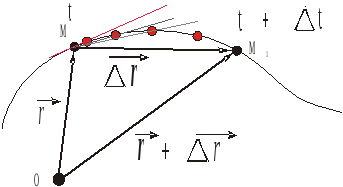
Видно, что при 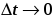секущая, по которой направлен вектор 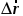, стремится к касательной к траектории точки. Следовательно,

вектор скорости точки всегда направлен по касательной к её траектории.

При координатном способе задания движения в декартовой системе координат вектор скорости определяется по проекциям на оси координат:

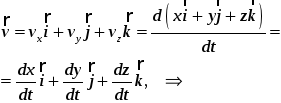
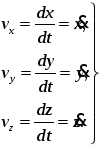44\* MERGEFORMAT ()

Модуль (величина) скорости

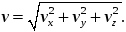55\* MERGEFORMAT ()

При естественном способе задания движения будет

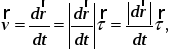
где 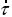– единичный вектор касательной, а

В этом равенстве 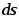– приращение длины дуги траектории точки.

Тогда, окончательно,

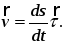66\* MERGEFORMAT ()

Выражение

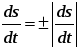77\* MERGEFORMAT ()

–это проекция вектора скорости на касательную, а

88\* MERGEFORMAT ()

это модуль (величина) скорости.

1. Ускорение точки.

Ускорение точки характеризует «быстроту» изменения скорости точки.

Формально: ускорение – это изменение скорости за единицу времени.

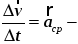99\* MERGEFORMAT ()

среднее ускорение точки за промежуток времени 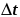, а

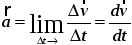1010\* MERGEFORMAT ()

называется ускорением точки в данный момент времени, или мгновенным ускорением точки, или, просто, ускорением точки.

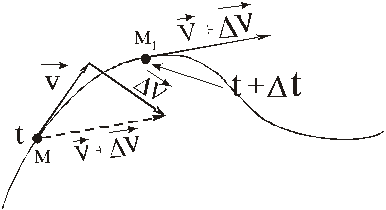
Из (18) видно, что вектор ускорения определяет изменение скорости точки как по модулю, так и направлению.

В силу этого вектор ускорения точки может быть расположен с той стороны от касательной, с которой расположена и сама кривая. Если в какой-то точке кривая расположена с двух сторон от касательной (точка перегиба), то вектор ускорения в этом случае направлен по касательной.

Учитывая формулу (11) из лекции 1 для вектора скорости

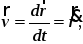
из (10) получим

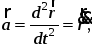1111\* MERGEFORMAT ()

т.е. вектор ускорения точки может быть найден как вторая производная по времени от радиус-вектора точки.

Координатный способ задания движения. Имеем:

Следовательно, сравнивая выражения слева и справа, получаем

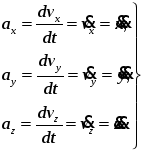1212\* MERGEFORMAT ()

Таким образом, при координатном способе задания вектор ускорения находится по проекциям на оси координат согласно формулам (12). После этого модуль ускорения находится по теореме Пифагора

1313\* MERGEFORMAT ()

Естественный способ задания движения.

Необходимо ввести естественный трёхгранник, который образуется следующим образом:

 с началом в текущем положении точки на траектории проводится касательная ; положительное направление выбирается в сторону возрастания функции s(t) и задаётся единичным вектором ;

 проводим перпендикуляр к касательной, расположенный в той же плоскости, в которой находится малая окрестность кривой и сама касательная; положительное направление выбираем в сторону вогнутости кривой и задаём единичным вектором 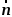; заданная таким образом ось называется главной нормалью к кривой;

 проводим перпендикуляр к касательной и главной нормали; этот перпендикуляр называется бинормалью к кривой и обозначается буквой b; положительное направление выбирается так, чтобы тройка векторов 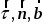была точно такой же, как и орты основной системы координат .

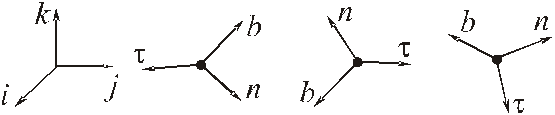
Полученная система координат 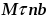и носит название естественного трёгранника. Эта система координат, в отличие от основной Oxyz, движется вместе с точкой по траектории.

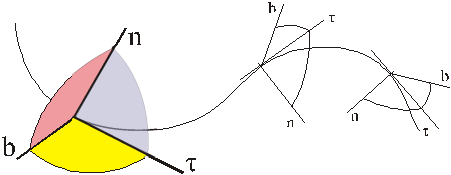
Положение естественного трёхгранника относительно основной системы координат Oxyz известно, если известна траектория (кривая).

Поэтому вектор ускорения точки при естественном способе находится по проекциям на оси естественного трёхгранника Mnb. Имеем

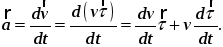
Так как 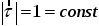, то

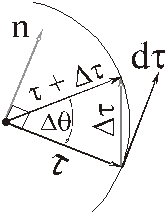
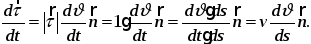
Производная 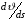называется кривизной кривой в данной точке:

Кривизна показывает, насколько сильно кривая в данной точке отличается от прямой линии.

Величина, обратная к кривизне:

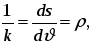
обозначается буквой 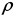и называется радиусом кривизны в данной точке.

На основании изложенного, получаем

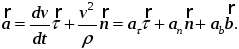1414\* MERGEFORMAT ()

Сравнивая левую и правую части равенства, заключаем:

проекция ускорения точки на касательную равна

1515\* MERGEFORMAT ()

и называется касательным ускорением точки;

проекция ускорения точки на главную нормаль равна

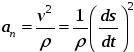1616\* MERGEFORMAT ()

и называется нормальным ускорением точки;

при любом движении точки проекция ускорения на бинормаль равна нулю !!

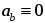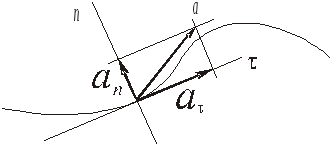
Формула (14) может быть переписана следующим образом:

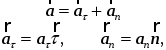1717\* MERGEFORMAT ()

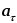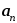а величины и определены равенствами (15) и (16):

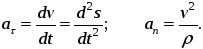
Физический смысл касательного и нормального ускорений:

 касательное ускорение определяет изменение скорости по модулю (или, другими словами, – изменение модуля скорости);

 нормальное ускорение определяет изменение направления вектора скорости.

Поскольку 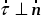и, следовательно, 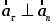, то модуль ускорения точки

1818\* MERGEFORMAT ()

О радиусе кривизны кривой: радиус кривизны – это радиус круга кривизны.