итог5

152

Тема 5. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ

Программный объем темы:

1. Функции нескольких переменных. Область определения. Предел функции. Непрерывность.

2. Частные производные. Полный дифференциал и его связь с част­ными производными. Инвариантность формы полного дифференциала. Касательная плоскость и нормаль к поверхности. Геометрический смысл полного дифференциала.

3. Скалярное поле. Производная по направлению. Градиент.

4. Частные производные и полные дифференциалы высших поряд­ков. Формула Тейлора.

5. Производные сложной функции. Неявные функции. Дифференци­рование неявных функций.

6. Экстремумы функций нескольких переменных. Необходимое ус­ловие. Достаточные условия.

7. Условный экстремум. Метод Лагранжа.

Существуют различные способы задания функции двух переменных:

а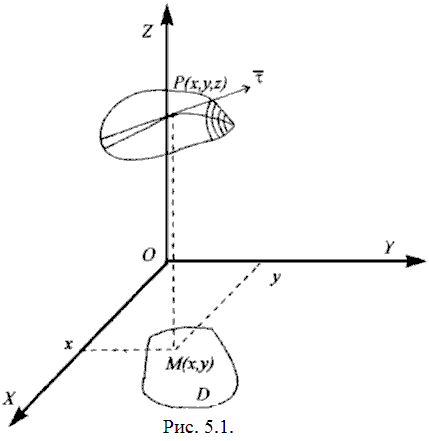) аналитическое задание - когда функция задана анали­тическим выражением, например,

б) табличное задание - с помощью таблицы, в которой на пересече­нии строки и столбца, соответствующих определенным значениям и , поставлено соответствующее значение функции ;

в) графическое изображение функции . Пусть эта функ­ция определена в области на плоскости , т.е. для таких пар чисел , что точка лежит в (рис. 5.1.). Условно можно записать . Из каждой такой точки восставим перпендикуляр к плоскости и отложим на нем отрезок, равный . Получим в про­странстве точку , где Множество таких точек при всевозможных называют гра­фиком функции , т.е. график - это поверхность с уравнением

Число называется пределом функции при (т.е., при , ), если разность можно сделать как угодно малой, взяв т. достаточно близко к т. . При этом пишут .

Функция называется непрерывной в т. , если

Пусть аргументы и функции получили приращение и . Частным приращением функции по (по ) и полным при­ращением называются разности

Частными производными по (по ) от функции назы­ваются

Отсюда видно, что есть производная по , вычисленная в пред­положении, что , а есть производная по , вычис­ленная в предположении, что .

Пример.

Аналогично определяются частные производные функций большого числа переменных.

Если то является сложной функцией от . При этом

и называется полной производной функции .

Пример.

Найти полную производную , если ,

Имеем

Подставляя найденные выражения в формулу полной производной, получим

В случае, когда функция задана неявно равенством , частные производные находятся по формулам:

Полным дифференциалом функции называется

Как и для дифференциала функции одного переменного, верно приближенное равенство (где – полное приращение).

Пример.

Вычислить приближенно с помощью дифференциала

Искомое число будем рассматривать как значение функции при , , если , . Имеем

Следовательно,

и поэтому искомое

Прямая линия называется касательной к поверхности с уравнением в точке , если она является касательной к ка­кой-либо кривой, лежащей на поверхности и проходящей через т. . Так как таких кривых бесконечно много, то и касательных к поверхности в т. бесконечно много. Если в т. производные существуют и непрерывны, причем хотя бы одна из них отлична от нуля, то все касательные прямые к данной поверхности в точке лежат в одной плоскости. Эта плоскость называется касательной плоскостью к поверх­ности в точке . Прямая, перпендикулярная к касательной плоскости и проходящая через т. , называется нормалью к поверхности. Оказывается, что касательная плоскость к поверхности в точке перпендикулярна вектору

Поэтому уравнения касательной плоскости и нормали имеют вид

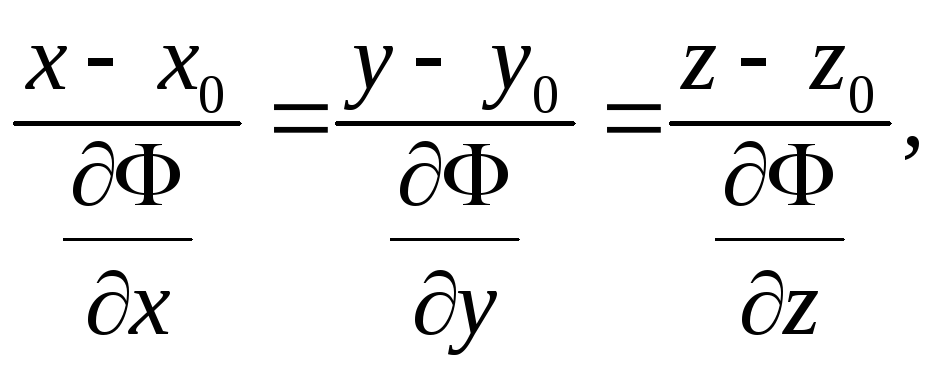
где значения вычисляются в т. .

Пример.

В точке провести касательную плоскость и нормаль к по­верхности, заданной уравнением

Так как то

После упрощений получим, что уравнение касательной плоскости имеет вид

,

а уравнение нормали

П

Рис. 5.2.

усть даны функция , точка и вектор . Пусть также - точка на векторе . Производной от функции в точке по направлению вектора называется

Эта производная выражается через частные производные так:

где

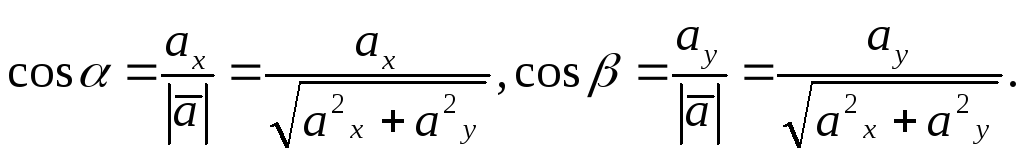
Введем вектор , который называется градиентом функции , а также вектор единичной длины . Тогда производную по направлению можно записать в виде

В случае функции трех переменных , точки и вектора производная по направлению также опре­деляется формулами (1), (3), но вместо (2) будет

Отметим следующее свойство производной по направлению: произ­водная в данной точке по направлению имеет наибольшее значение, если направление вектора совпадает с направлением градиента; это наибольшее значение производной равно .

Пример.

Дана функция , точка и вектор . Найти: 1) в точке ; 2) производную в точке по направлению вектора .

Вычислим частные производные функции в точке :

Поэтому

Возьмем теперь вектор . Так как то

Вторые частные производные (или частные производные 2-го по­рядка) от функции , определяются так:

Можно показать, что .

Если функция достигает экстремума в т. , то каждая из частных производных и , в т. или не существует, или обращается в нуль. Эти условия аналогичны необходимому условию экстремума функции одного переменного. Точки, в которых и не существуют или равны нулю, называются критическими точками функ­ции . Каждая точка экстремума является критической точкой, но не каждая критическая точка — точка экстремума.

Обозначим Пусть — критическая точка, причем Тогда в точке : 1) имеет максимум, если и ; 2) имеет минимум, если и ;

3) не имеет экстремума, если .

4) если , то экстремум может быть и может не быть (требуется дальнейшее исследование).

Пример.

Дана функция

Требуется исследовать данную функцию на экстремум в области , ограниченной линиями , найти точки и со­ответственно наименьшего и наибольшего значений функции в области и подсчитать эти значения.

Построим данную область (рис. 5.3.).

Найдем критические точки внутри области:

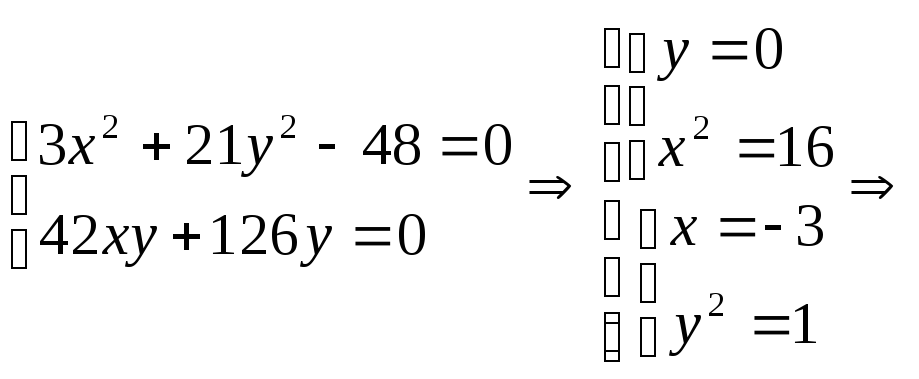
Из этих точек лишь только принадлежит области . В ней имеем

Поэтому и . Следовательно, - точка экстремума, а именно - точка минимума. Вычислим значение функции в этой точке:

Найдем теперь наибольшее и наименьшее значения функции в об­ласти . Для этого рассмотрим каждый участок границы :

а)

при и

Вычислим значения функции в точках

б)

при

Значение функции в т. известно.

Вычислим функцию в т. :

в)

Вычисления показывают, что при .

Сравнивая найденные в точках значения функ­ции, получаем (в точке ), (в точке ).

Таким образом,

Контрольная работа №5 по теме

"ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ"

5.1. Дана функция . Найти частные производные .

5.1.1.

5.1.2.

5.1.3.

5.1.4.

5.1.5.

5.1.6.

5.1.7.

5.1.8.

5.1.9.

5.1.10.

5.2. Вычислить значение производной сложной функции , где , при .

5.2.1.

5.2.2.

5.2.3.

5.2.4.

5.2.5.

5.2.6.

5.2.7.

5.2.8.

5.2.9.

5.2.10.

5.3. Функция задана в неявном виде. Найти полный дифференциал функции .

5.3.1.

5.3.2.

5.3.3.

5.3.4.

5.3.5.

5.3.6.

5.3.7.

5.3.8.

5.3.9.

5.3.10.

5.4. Дана функция . Показать, что справедливо указанное в задаче соотношение.

5.4.1.

5.4.2.

5.4.3.

5.4.4.

5.4.5.

5.4.6.

5.4.7.

5.4.8.

5.4.9.

5.4.10.

5.5. Дана функция и две точки

Требуется:

1. вычислить значение 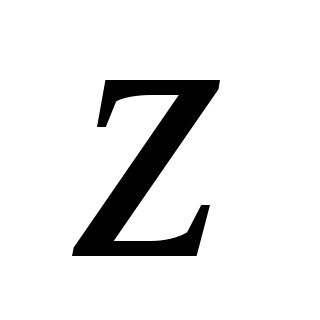в т. ;

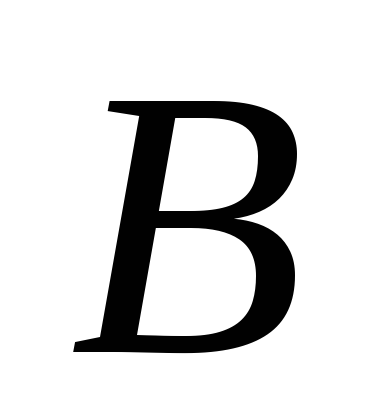2. вычислить приближенное значение функции в т. 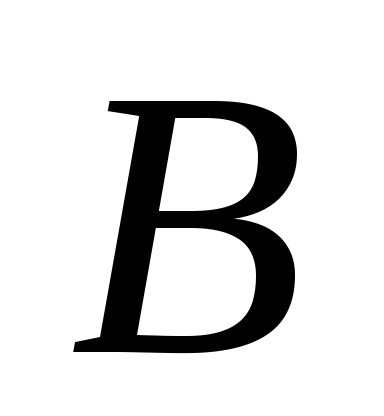, исходя из значения функции в точке и заменив приращение функции при переходе от точки к точке 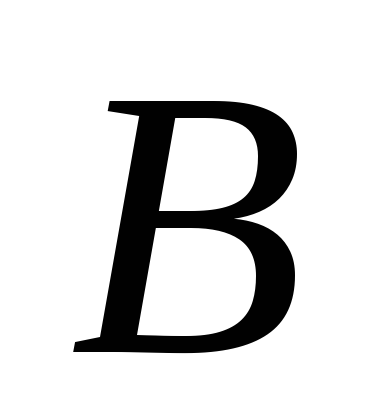её дифференциалом;

3. оценить в процентах относительную погрешность, получающуюся при замене приращения функции её дифференциалом;

4. составить уравнение касательной плоскости к поверхности в точке .
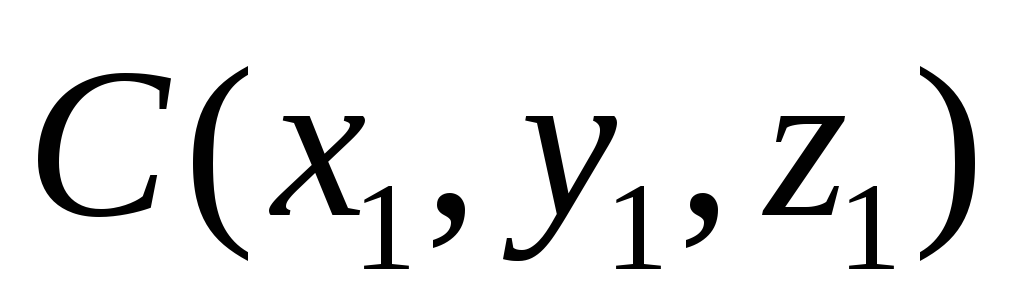