
- •Мера Лебега. Интеграл Лебега. Пространства суммируемых по Лебегу функций.
- •1.2. Мера Лебега ограниченных множеств на числовой прямой.
- •1.3. Свойства измеримых по Лебегу множеств.
- •1.4. Примеры измеримых и не измеримых подмножеств.
- •Упражнения к главе 1.
- •Глава 2. Интеграл Лебега.
- •2.1. Измеримые функции.
- •2.2. Последовательности измеримых функций.
- •Упражнение к главе 2.
- •Глава 3. Интеграл Лебега.
- •3.1. Интеграл Лебега от ограниченной функции.
- •3.2. Основные свойства интеграла Лебега.
- •3.3. Интеграл Лебега от неотрицательной измеримой функции.
- •3.4. Интеграл Лебега от произвольной измеримой функции.
- •Упражнения к главе 3.
- •Глава 4. Пространства суммируемых функций.
- •4.1. Пространство суммируемых функций.
- •4.2. Пространство функций суммируемых с квадратом.
- •4.3. Пространство функций, суммируемых со степенью p.
- •Упражнения к главе 3.
Мера Лебега. Интеграл Лебега. Пространства суммируемых по Лебегу функций.
С О Д Е Р Ж А Н И Е
Глава 1. Мера Лебега.
1.0. Вспомогательные определения и утверждения.
Структура открытых и замкнутых множеств на числовой прямой.
Мера Лебега ограниченных множеств на числовой прямой.
Свойства измеримых по Лебегу множеств.
Классы измеримых множеств.
Упражнения к главе 1.
Глава 2. Измеримые функции.
2.1. Измеримые функции.
2.2. Свойства измеримых функций.
2.3. Последовательности измеримых функций.
Упражнения к главе 2.
Глава 3. Интеграл Лебега.
3.1. Интеграл Лебега от ограниченной функции. Свойства интеграла Лебега.
3.2. Интеграл Лебега от неограниченной неотрицательной функции.
3.3. Интеграл Лебега от произвольной измеримой функции.
Упражнения к главе 3.
Глава 4. Суммируемые функции.
4.1. Пространство суммируемых функций.
4.2. Пространство суммируемых с квадратом функций.
4.3. Пространство
![]() .
.
Упражнения к главе 4.
Глава 1. Мера Лебега.
1.0. Вспомогательные определения и утверждения.
В этом параграфе мы приведем необходимые
для дальнейшего изложения понятия о
множествах являющихся подмножествами
множества действительных чисел
![]() (так называемые линейные множества).
(так называемые линейные множества).
В частности нам потребуется понятия открытого и замкнутого множества. В топологии понятие открытого множества вводится аксиоматически. Однако, учитывая простоту рассматриваемых множеств, в изложении мы будем избегать аксиоматического определения открытых множеств.
Элементами рассматриваемых множеств
являются числа, поэтому не возникает
недоразумений при отождествлении
элемента
![]() с точкой на числовой оси, имеющей
координату
с точкой на числовой оси, имеющей
координату![]() .
.
Множества
![]() ,
,![]() ,
,![]() ,
,![]()
будем называть соответственно отрезком, интервалом, полуинтервалом с включенным левым концом, полуинтервалом с включенным правым концом.
Для элемента
![]() интервал вида
интервал вида![]() будем называть
будем называть![]() -окрестностью
элемента и обозначать
-окрестностью
элемента и обозначать![]() .
.
Точка
![]() называется внутренней точкой множества,
если существует
называется внутренней точкой множества,
если существует![]() -окрестность
элемента принадлежащая множеству
-окрестность
элемента принадлежащая множеству![]() .
.
Множество
![]() называется дополнением множества
называется дополнением множества![]() .
.
Множество
![]() ,
имеющее открытое дополнение называется
замкнутым.
,
имеющее открытое дополнение называется
замкнутым.
Утверждение 1. Объединение открытых множеств является открытым множеством. Пересечение конечного числа открытых множеств есть открытое множество.
Утверждение 2. Объединение конечного числа замкнутых множеств, является замкнутым множеством, пересечение любого числа замкнутых множеств есть замкнутое множество.
Точной нижней гранью множества
![]() называется такое число
называется такое число![]() ,
что
,
что
для любого
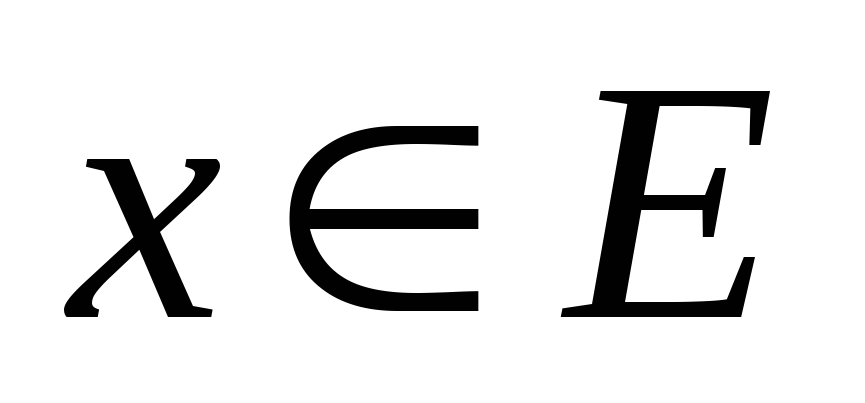 справедливо неравенство
справедливо неравенство ;
;для любого
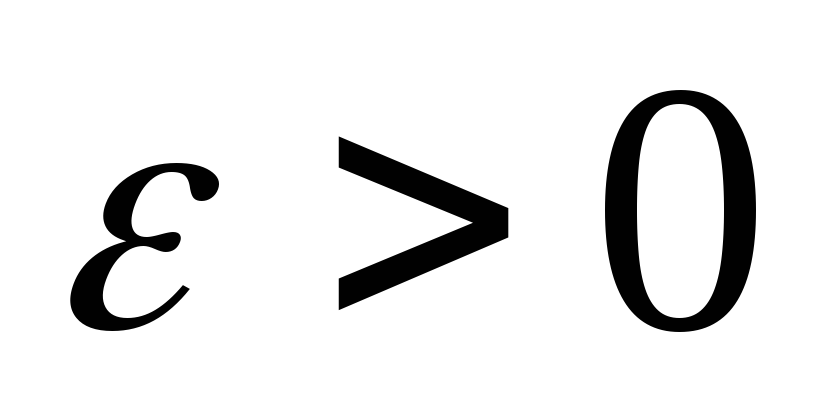 найдется такой элемент
найдется такой элемент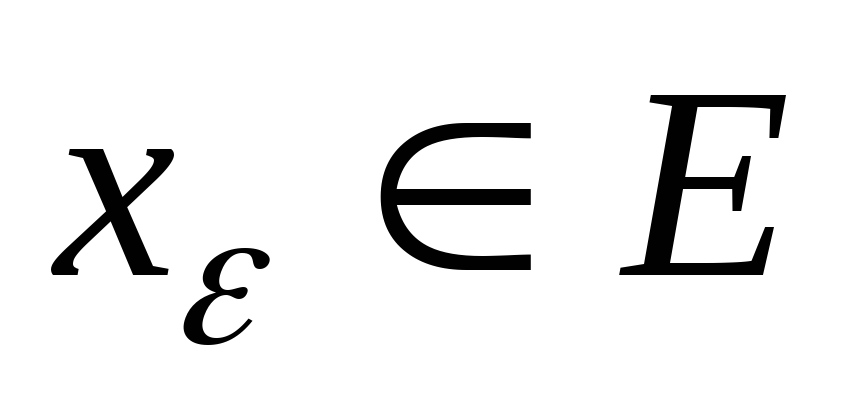 ,
что
,
что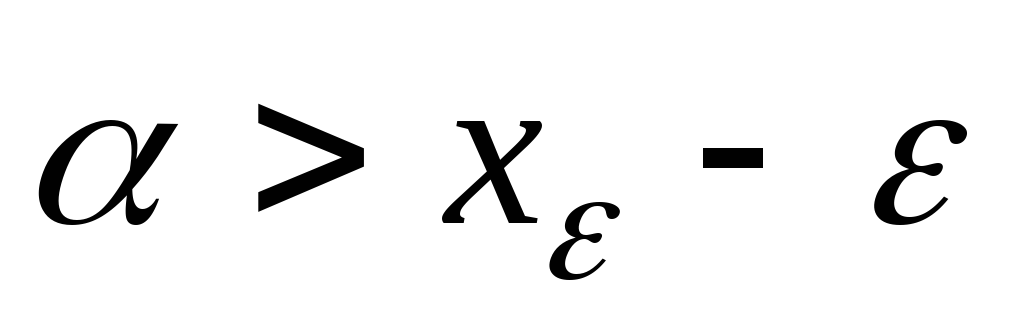 .
.
Точную нижнюю грань множества
![]() будем обозначать
будем обозначать![]() .
.
Точной верхней гранью множества
![]() называется такое число
называется такое число![]() ,
что
,
что
для любого
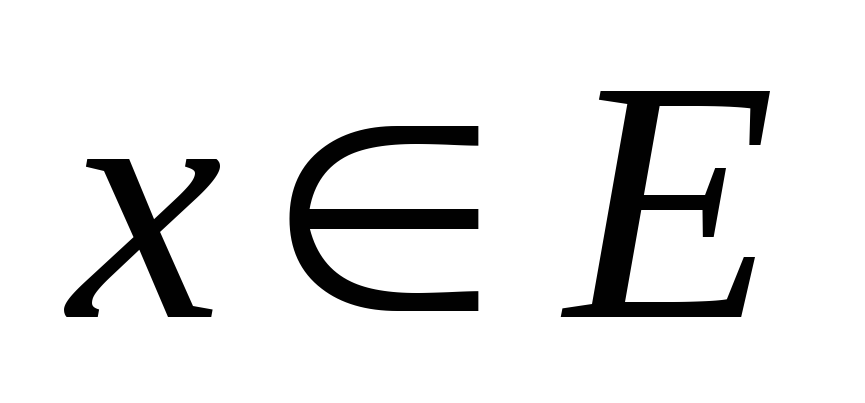 справедливо неравенство
справедливо неравенство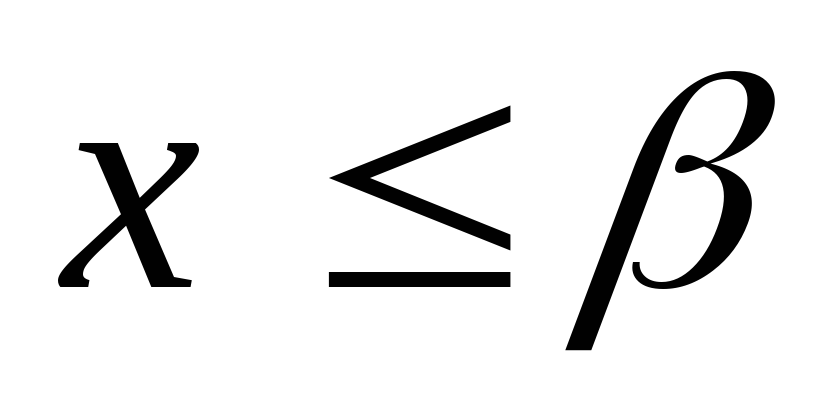 ;
;для любого
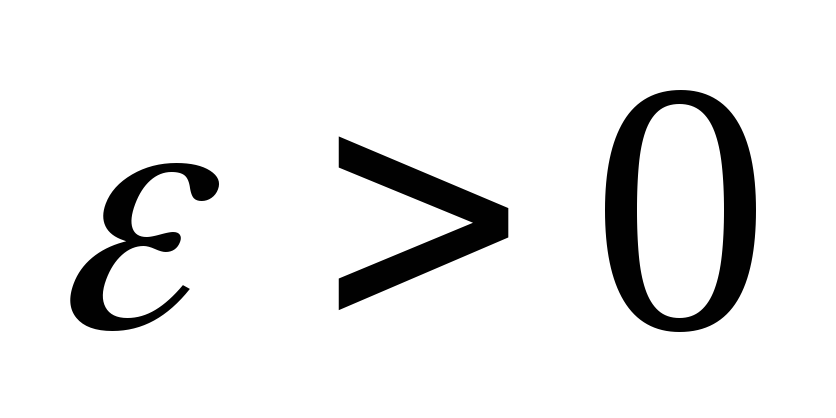 найдется такой элемент
найдется такой элемент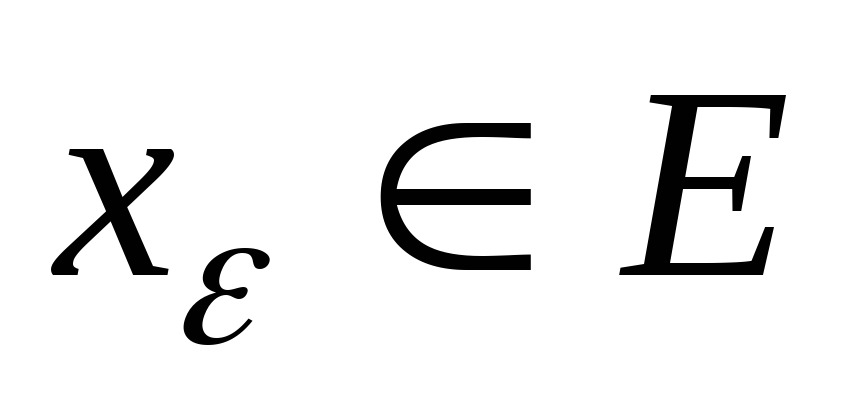 ,
что
,
что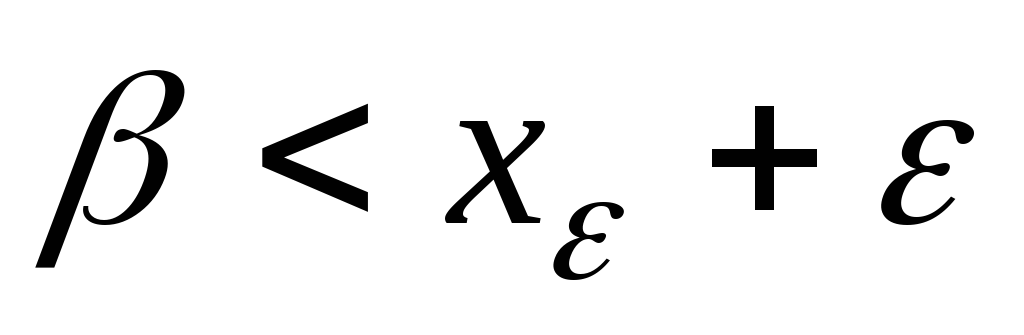 .
.
Точную верхнюю грань множества
![]() будем обозначать
будем обозначать![]() .
.
Для любого замкнутого числового
множества
![]()
![]() .
Поэтому точные нижнюю и верхнюю грани
замкнутого множества будем обозначать
соответственно
.
Поэтому точные нижнюю и верхнюю грани
замкнутого множества будем обозначать
соответственно![]() .
.
Множество
![]() называется ограниченным, если найдется
такое число
называется ограниченным, если найдется
такое число![]() ,
что
,
что![]() .
.
Символом
![]() будем обозначать множество рациональных
чисел.
будем обозначать множество рациональных
чисел.
Структура открытых и замкнутых множеств на числовой прямой.
Пусть
![]() - некоторое подмножество множества
- некоторое подмножество множества![]() .
.
Определение 1.1.1.Интервал![]() называетсясоставляющим интервалом
множества
называетсясоставляющим интервалом
множества![]() ,
если
,
если
1)
![]() ,
,
2)
![]() .
.
Например, множество
![]() не имеет составляющих интервалов, а
множество
не имеет составляющих интервалов, а
множество![]() имеет один составляющий интервал
имеет один составляющий интервал![]() .
.
Справедлива
Лемма 1.1.1. Два составляющих интервала одного множества или не пересекаются, или совпадают.
Доказательство. Пусть множество![]() имеет два пересекающихся составляющих
интервала
имеет два пересекающихся составляющих
интервала![]() и
и![]() ,
т.е. существует такое число
,
т.е. существует такое число![]() ,
что
,
что![]() и
и![]() .
Иными словами, концы интервалов
удовлетворяют соотношению
.
Иными словами, концы интервалов
удовлетворяют соотношению![]() .
.
Если
![]() ,
то
,
то![]() ,
поэтому
,
поэтому![]() .
Таким образом, интервал
.
Таким образом, интервал![]() не является составляющим интервалом
множества
не является составляющим интервалом
множества![]() .
Полученное противоречие приводит к
выводу, что предположение
.
Полученное противоречие приводит к
выводу, что предположение![]() не верно.
не верно.
Если
![]() ,
то
,
то![]() .
Отсюда следует, что
.
Отсюда следует, что![]() не является составляющим интервалом
множества
не является составляющим интервалом
множества![]() .
Полученное противоречие отвергает
предположение
.
Полученное противоречие отвергает
предположение![]() .
.
Таким образом,
![]() .
.
Проводя аналогичные рассуждения
относительно левых концов составляющих
интервалов, приходим к выводу
![]() .
.
Доказано, что два составляющих интервала имеющие непустое пересечение совпадают.
Структура любого открытого ограниченного множества на числовой прямой описана в следующей теореме.
Теорема 1.1.1. Каждое непустое ограниченное открытое множество на прямой представимо в виде объединения не более чем счетного числа составляющих интервалов.
Доказательство.Пусть![]() - ограниченное непустое открытое
множество. И пусть
- ограниченное непустое открытое
множество. И пусть![]() - произвольная точка множества. Покажем
существование составляющего интервала,
содержащего точку
- произвольная точка множества. Покажем
существование составляющего интервала,
содержащего точку![]() .
В силу открытости и ограниченности
множества
.
В силу открытости и ограниченности
множества![]() ,
множество
,
множество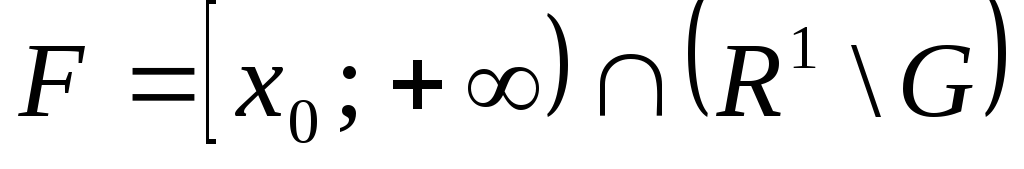 является непустым замкнутым множеством.
Множество
является непустым замкнутым множеством.
Множество![]() ограничено снизу числом
ограничено снизу числом![]() ,
т.е. для любого
,
т.е. для любого![]() справедливо неравенство
справедливо неравенство![]() .
Следовательно, существует
.
Следовательно, существует![]() .
Но так как
.
Но так как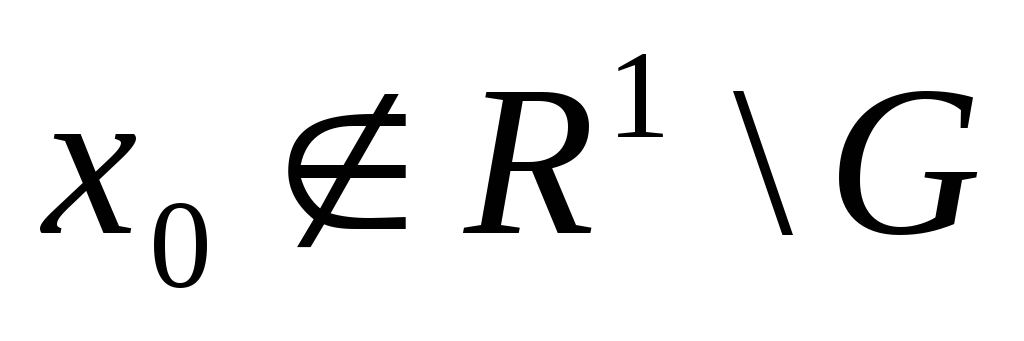 ,
то
,
то![]() .
.
Предположим, что
![]() ,
тогда существует такой
,
тогда существует такой![]() ,
что
,
что![]() и
и![]() .
Очевидно, что
.
Очевидно, что![]() .
Поэтому
.
Поэтому![]() .
Таким образом, элемент
.
Таким образом, элемент![]() удовлетворяет двум противоречащим
неравенствам. Следовательно, предположение
удовлетворяет двум противоречащим
неравенствам. Следовательно, предположение![]() не верно.
не верно.
Аналогично можно показать существование
такого
![]() ,
что
,
что![]() и
и![]() .
.
Таким образом, показано существование
такого интервала
![]() ,
что
,
что![]() и
и![]() ,
,![]() .
По определению,
.
По определению,![]() является составляющим интервалом
множества
является составляющим интервалом
множества![]() .
Согласно лемме 1.1.1 каждая точка множества
попадает только в один интервал.
.
Согласно лемме 1.1.1 каждая точка множества
попадает только в один интервал.
Для доказательства того факта, что любое ограниченное открытое множество представимо в виде объединения не более чем счетного числа составляющих интервалов, выберем в каждом составляющем интервале по одному рациональному числу. Тем самым установим взаимнооднозначное соответствие между числом составляющих интервалов и некоторым подмножеством множества рациональных чисел.
В силу того, что любое подмножество рациональных чисел не более чем счетно, можно сделать вывод, что число составляющих интервалов любого ограниченного открытого множества не более чем счетно.
Теорема доказана.
Отметим справедливость обратного утверждения:
Всякое множество являющееся объединением не более чем счетного числа взаимно не налегающих интервалов, является открытым.
Рассмотрим ограниченное замкнутое
множество
![]() на числовой прямой.
на числовой прямой.
Числа
![]() и
и![]() определим равенствами
определим равенствами
![]()
В силу ограниченности множества
![]() числа
числа![]() ,
,![]() конечны и
конечны и![]() .
.
Дополнение
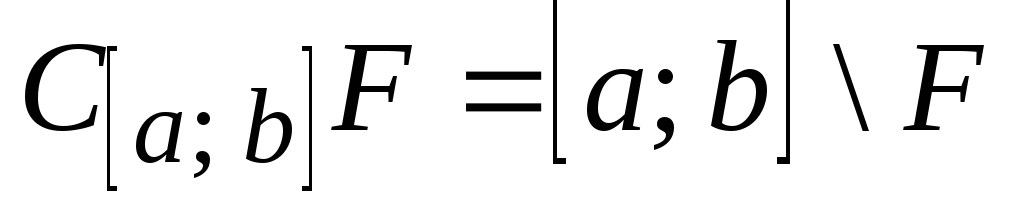 множества
множества![]() до отрезка
до отрезка![]() является открытым и имеет структуру,
описанную в теореме 1.1.1. Поэтому
справедлива
является открытым и имеет структуру,
описанную в теореме 1.1.1. Поэтому
справедлива
Теорема 1.1.2.Всякое непустое замкнутое
ограниченное множество![]() на прямой или является отрезком, или
получается из некоторого отрезка
удалением не более чем счетного числа
не налегающих интервалов, концы которых
принадлежат множеству
на прямой или является отрезком, или
получается из некоторого отрезка
удалением не более чем счетного числа
не налегающих интервалов, концы которых
принадлежат множеству![]() .
.
Отметим, что изолированные точки замкнутого множества появляются при удалении двух интервалов с общим концом.
