1. Концепция метода конечных элементов

Метод конечных элементов основан на идее аппроксимации непрерывной функции (температуры, электрического потенциала, скорости, давления, перемещения и т.д.) дискретной моделью, которая строится на множестве кусочно-непрерывных функций, определенных на конечном числе подобластей, называемых элементами. Элементы в исследуемой области связаны между собой общими узловыми точками. В качестве функций элемента чаще всего применяется полином. Порядок полинома зависит от числа используемых в каждом узле элемента данных о непрерывной функции.

В общем случае непрерывная величина заранее неизвестна и нужно определить значения этой величины в некоторых внутренних точках области. Дискретную модель можно построить, если сначала предположить, что числовые значения этой величины в каждой внутренней точке области известны. После этого можно перейти к общему случаю. При построении дискретной модели непрерывной величины поступают следующим образом:

В рассматриваемой области фиксируется конечное число точек. Эти точки называются узловыми точками или просто узлами.

Значения непрерывной величины в каждой узловой точке считается переменной, которая должна быть определена.

Область определения непрерывной величины разбивается на конечное число подобластей, называемых элементами. Эти элементы имеют общие узловые точки и в совокупности аппроксимируют форму области.

Непрерывная величина аппроксимируется на каждом элементе полиномом, который определяется с помощью узловых значений этой величины. Для каждого элемента определяется свой полином, но полиномы подбираются таким образом, чтобы сохранялась непрерывность величины вдоль границы элемента. Этот полином, связанный с каждым элементом назовем функцией элемента.

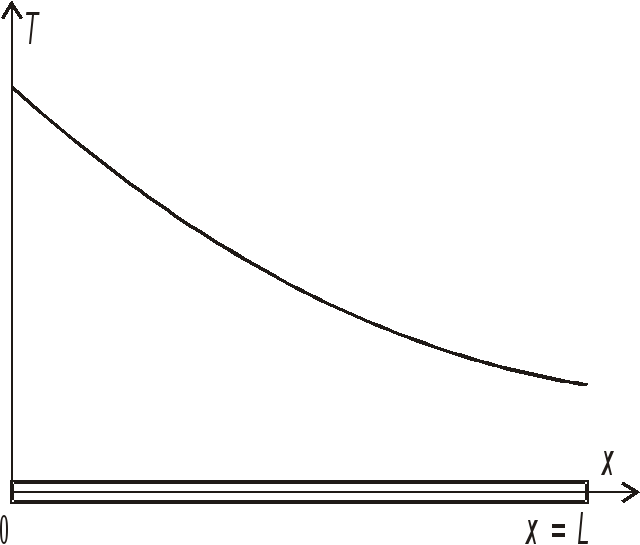
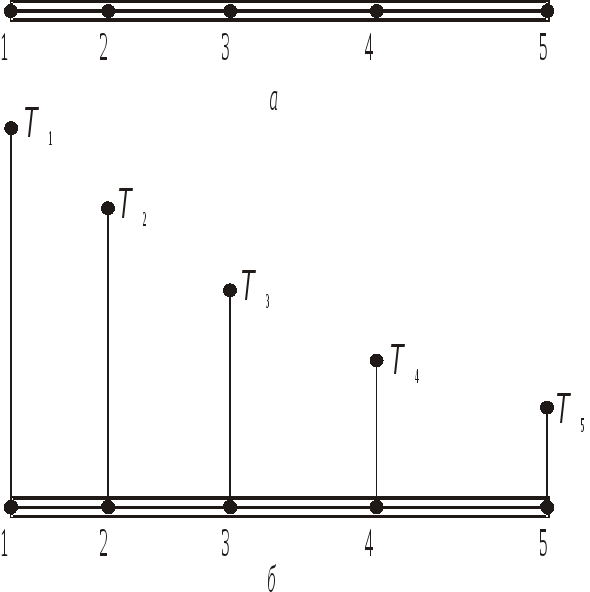
Основная концепция метода конечных элементов может быть наглядно проиллюстрирована на одномерном примере заданного распределения температуры в стержне, показанном на рис. 1.1. Рассматривается непрерывная величина , область определения – отрезоквдоль оси. Фиксированы и пронумерованы пять точек на оси(см. рис. 1.2,а). Это узловые точки. Они могут быть расположены на разном расстоянии друг от друга. Количество узлов может быть произвольным. Значенияв данном случае известны в каждой узловой точке. Эти фиксированные значения представлены на рис. 1.2,б. и обозначены в соответствии с номерами узловых точек через,, …,.

Рис. 1.1. Распределение температуры в одномерном стержне

Рис. 1.2. Узловые точки и предполагаемые значения

Разбиение области на элементы может быть проведена двумя различными способами. Можно, например, ограничить каждый элемент двумя соседними узловыми точками, образовав четыре элемента (см. рис. 1.3, а) или разбить область на два элемента, каждый из которых содержит три узла (см. рис. 1.3,б). Соответствующий элементу полином определяется по значениямв узловых точках элемента. В случае разбиения области на четыре элемента, когда на каждый элемент приходится по два узла, функция элемента будет линейна по(две точки однозначно определяют прямую линию). Окончательная аппроксимациябудет состоять из четырех кусочно-линейных функций, каждая из которых определена на отдельном элементе.

Рис. 1.3. Деление области на элементы

Другой способ разбиения области на два элемента с тремя узловыми точками приводит к представлению функции элемента в виде полинома второй степени. В этом случае окончательной аппроксимацией будет совокупность двух кусочно-непрерывных квадратичных функций. Отметим, что это приближение будет именно кусочно-непрерывным, так как углы наклона графиков обеих функций могут иметь разные значения в третьем узле.

В общем случае распределение температуры неизвестно и мы хотим определить значения этой величины в некоторых точках. Методика построения дискретной модели остается точно такой же, как описано выше, но с добавлением одного дополнительного шага. Снова определяются множество узлов и значения температуры в этих узлах ,,, …, которые теперь являются переменными, так как они заранее неизвестны. Область разбивается на элементы, на каждом из которых определяются соответствующая функция элемента. Узловые значениядолжны быть теперь подобраны таким образом, чтобы обеспечивалось «наилучшее» приближение к истинному распределению температуры. Этот подбор осуществляется путем минимизации некоторой величины, связанной с физической сущностью задачи, например, с помощью использования методов наименьших квадратов, метод Ритца, метод Галёркина или других [123–128]. В результате процесс минимизации задача сводится к решению системы линейных алгебраических уравнений относительно узловых значений.

При построении дискретной модели непрерывной величины определенной в двух- или трехмерной области, основная концепция метода конечных элементов используется аналогично. В двухмерном случае элементы описываются функциями от ,, при этом чаще всего рассматриваются элементы в форме треугольника или четырехугольника.