
Тема_3_Нелин_ур_Inf_2
.pdf
Лекция 2
Тема 3. Решение нелинейных уравнений
В различных инженерных и исследовательских задачах часто возникает необходимость нахождения одного или нескольких решений уравнений вида
Y( x ) =0, |
(3.1) |
где Y(x) - некоторая известная функция независимой переменной x. В определение функции Y(x) могут входить параметры, имеющие постоянные значения в каждой конкретной реализации функции. Например, функция
Y( x ) =ax2 +bx +c , |
(3.2) |
определяет множество многочленов второго порядка. Описание многочлена содержит одну независимую переменную – аргумент x, значения которой принадлежат диапазону [X0B ,B XkB ]B и три параметра a, b, c, не зависящие друг от друга.
Набор числовых значений этих трех параметров определяет одну реализацию, для которой по известным алгебраическим формулам могут быть вычислены значения двух корней.
РешениямиU U или корнямиU уравненияU (3.1), называются
значения аргумента х, обращающие равенство (3.1) в тождество.
Функции Y(x) могут быть алгебраическими или трансцендентными [1].
Алгебраическими называются уравнения, которые путем алгебраических преобразований могут быть приведены к канонической полиномиальной форме
Pn (x) = a0 + a1 x + a2 x2 +K+ an−1 xn−1 + an xn |
(3.3) |
В общем случае аналитическое решение может быть получено для алгебраических уравнений не выше четвёртого порядка [12]. Существуют аналитические формулы для решения:
-линейных уравнений a*x+b=0 (или a0B B + a1B *xB = 0);
-квадратных уравнений a *x2P P + b*x + c = 0 (или a0B B + a1B *xB + a2B *xB 2P =P 0);
-кубичных уравнений a0B B + a1B *xB + a2B *xB 2P P + a3B *xB 3P P = 0 и
-уравнений четвертой степени a0B B + a1B *xB + a2B *xB 2P P + a3B *xB 3P P + a4B *xB 4P P = 0.
Для линейного уравнения a*x+b=0 существует одно очевидное решение x=b ⁄ a при a ≠ 0.
20 |
02.11.2010 / Любимов Е.Б. |

Лекция 2
Для квадратного уравнения a*x2P P + b*x + c = 0 в зависимости от значения детерминанта D=(b2 – 4*a*c) решения находятся по алгоритму, определяемому соотношениями приводимыми ниже:
─ если D >0, то |
x1,2 = |
−b ± |
D , |
|
||||
|
|
|
2a |
b |
|
|
|
|
─ |
если D=0, то |
x1 = x2 = − |
, |
(3.4) |
||||
2a |
||||||||
|
|
|
|
|
|
|||
─ |
если D<0, то |
x1,2 |
= − b |
±i |
|
D . |
||
|
|
|
2a |
|
|
2a |
||
Описание алгоритмов решения кубичных уравнений и уравнений четвертой степени имеется в [11] и [12].
3.1. Постановка задачи
Кроме алгебраических уравнений к нелинейным уравнениям, решения которых приходится искать при выполнении математических исследований различных технических систем, относятся также трансцендентные уравнения.
ТрансцендентнымU U уравнениям называются уравнения, неприводимые к виду алгебраических. В частности это уравнения, в которые входят тригонометрические, логарифмические и т.п. функции. Иногда для того, чтобы отличить эти уравнения от дифференциальных или интегральных уравнений их называют
"конечнымиU "U [2].
Для трансцендентных и алгебраических уравнения, порядок которых выше четвёртого, аналитические решения могут быть получены только в некоторых частных случаях. По этой причине математиками было разработано множество методов, позволяющих получать численные решения такого рода уравнений.
Алгоритмы численных методов решения нелинейных уравнений имеют итерационныйU характер.U То есть решение находится за несколько последовательно выполняемых шагов, каждый из которых должен увеличивать точность решения.
В ряде случаев функции, для которых необходимо найти решения, получены в результате экспериментальных исследований. Такие функции не имеют аналитических описаний, а задаются числовыми таблицами (таблично-заданные, табличные,
решетчатые функции). В таблицы записываются последовательные значения аргумента и соответствующие им значения исследуемой
21 |
02.11.2010 / Любимов Е.Б. |

Лекция 2
функции. На основании таблицы значений функции необходимо определить значение её корня.
Один из возможных вариантов алгоритма решения предусматривает построение по таблице аналитическойU
аппроксимирующейU илиU U интерполирующейU U функцииU U и нахождение решений для этой аналитической функции.
3.2. Общий подход к решению нелинейных уравнений
Численное решение нелинейного уравнения обычно осуществляется в 2 этапа:
1U этапU – отделение корней состоит в выделении на заданном интервале изменения аргумента [X0B ,B XkB ]B подынтервалов, содержащих только один корень. Для отделения корней обычно выполняется вычисление таблицы значений функции и (или) построение её графика;
2U этапU - уточнение корней выполняется на каждом промежутке, содержащем один корень, выделенном на первом этапе исследования поведения функции. Для уточнения значения корня выбирается один из численных методов. Наиболее часто используются метод половинного деления (дихотомии), метод хорд, метод касательных (Ньютона) и др.
3.2.1. Выполнение этапа отделения корней
Первый этап исследования функции – этап отделения корней предусматривает проведение анализа её поведения по графику и (или) по таблице её значений.
Исследование функции F(x) обычно выполняется в пределах ограниченного диапазона значений [X0 , Xk], определяемого исходя либо из каких-то соображений, определяемых физической сущностью решаемой задачи.
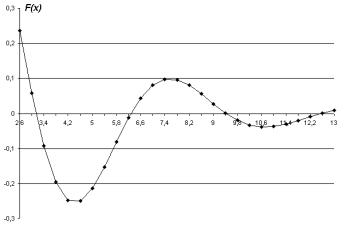
Вкачестве примера рассмотрим процедуру анализа при отделении корней функции F(x), график которой приведён на рис. 3.1.
Впределах заданного на графике интервала изменения аргумента х (от 0 до 13) функция 4 раза пересекает ось абсцисс, т.е. на этом интервале имеется четыре корня уравнения (3.1). Таким образом, на заданном интервале изменения аргумента мы можем
выделить четыре подынтервала [x0iB ,B xkiB ]B (i = 1,2,3,4), на каждом из которых находится один единственный корень.
22 |
02.11.2010 / Любимов Е.Б. |
Лекция 2
В точках, являющихся корнями функции, происходит смена знака функции (см. рис. 3.1). Т.е. условие, определяющее наличие корня в заданном интервале, может быть записано как
B B |
B B |
(3.5) |
F(x0i) * F(xki) < 0. |
|
|
Рис. 3.1. График исследуемой функции F(x)
Выполнив предварительный анализ, мы можем оценить точность решения по значению шага h =(xi+1B -B xiB )B , использованного при построении графика или таблицы значений исследуемой функции.
Решение можно считать найденным, если |
|
| F(x) | ≤ ε , |
(3.6) |
где ε - некоторая положительная вещественная константа, либо, если
| h | = |(xi+1B -B xiB )|B ≤ δ. |
(3.7) |
h - интервал неопределённости, в пределах которого находится точка перемены знака функцией F(x), т.е. выполняется условие (3.5). Однако выполнение по отдельности каждого из условий (3.6)
или (3.7) может оказаться недостаточным для определения корня функции F(x).
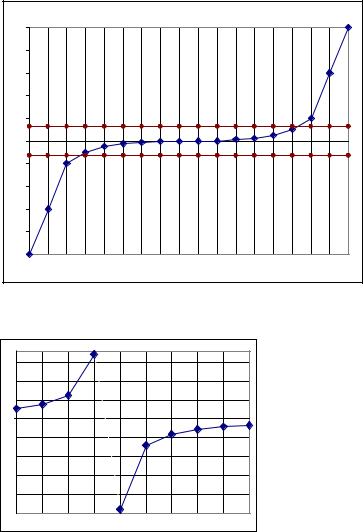
На рис. 3.2 показан график функции, для которой при выполнении условия (3.6) решение нельзя считать найденным. Диапазон значений аргумента х, в пределах которого для этой функции выполняется условие (3.6) равен [0,4; 1,5]. Таким образом длина интервала неопределённости равна (1,5-0,4)=1,1. Очевидно, что в этом случае нельзя считать корень найденным.
На рис. 3.3. показана функция, для которой нельзя считать решение найденным, не смотря на выполнение условия (3.7). В частности к таким функциям относятся функции, имеющие разрывы, с переменой знака.
23 |
02.11.2010 / Любимов Е.Б. |
X |
F(X) |
+eps |
-eps |
0,1 |
-0,5000000 |
0,065 |
-0,065 |
0,2 |
-0,3000000 |
0,065 |
-0,065 |
0,3 |
-0,1000000 |
0,065 |
-0,065 |
0,4 |
-0,0500000 |
0,065 |
-0,065 |
0,5 |
-0,0250000 |
0,065 |
-0,065 |
0,6 |
-0,0125000 |
0,065 |
-0,065 |
0,7 |
-0,0062500 |
0,065 |
-0,065 |
0,8 |
-0,0003125 |
0,065 |
-0,065 |
0,9 |
-0,0001550 |
0,065 |
-0,065 |
1 |
0,0001550 |
0,065 |
-0,065 |
1,1 |
0,0003125 |
0,065 |
-0,065 |
1,2 |
0,0062500 |
0,065 |
-0,065 |
1,3 |
0,0125000 |
0,065 |
-0,065 |
1,4 |
0,0250000 |
0,065 |
-0,065 |
1,5 |
0,0500000 |
0,065 |
-0,065 |
1,6 |
0,1000000 |
0,065 |
-0,065 |
1,7 |
0,3000000 |
0,065 |
-0,065 |
1,8 |
0,5000000 |
0,065 |
-0,065 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Лекция 2 |
|
F(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-0,1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-0,2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-0,3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-0,4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-0,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1 |
1,1 |
1,2 |
1,3 |
1,4 |
1,5 |
1,6 |
1,7 |
1,8 |
Рис. 3.2. Вид функции, решение которой нельзя считать найденным при |F(x)|<ε
Х |
F2(X) |
-3,5 |
2,670 |
-3,4 |
3,783 |
-3,3 |
6,260 |
-3,2 |
17,102 |
-3,1 |
-24,029 |
-3,0 |
-7,015 |
-2,9 |
-4,058 |
-2,8 |
-2,813 |
-2,7 |
-2,115 |
-2,6 |
-1,662 |
|
Tan(X+Pi/2) |
|
|
|
|
|
|
|
|
15 |
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
-5 |
|
|
|
|
|
|
|
|
|
-10 |
|
|
|
|
|
|
|
|
|
-15 |
|
|
|
|
|
|
|
|
|
-20 |
|
|
|
|
|
|
|
|
|
-25 |
|
|
|
|
|
|
|
|
|
-3,5 |
-3,4 |
-3,3 |
-3,2 |
-3,1 |
-3,0 |
-2,9 |
-2,8 |
-2,7 |
-2,6 |
Рис. 3.3. График функции, имеющей разрыв с переменой знака
На этапе предварительного анализа точность получаемого решения определяется точностью исходной таблицы значений исследуемой функции. В общем случае такая точность решения не достаточна.
3.2.2. Методы уточнения корней
При проведении процедуры отделения корней на заданном интервале изменения аргумента [Xнач ; Xкон] выделяется один или несколько подынтервалов [ajB ,B bjB ]B (j=1,2, …, m), на границах которых исследуемая функция меняет знак.
Уточнение корней может быть выполнено после отделения корней. На каждом, выделенном в результате проведения процедуры отделения корней, интервале [ajB ,B bjB ]B находится один корень, значение которого необходимо определить с точностью, задаваемой условиями
(3.6) или (3.7).
24 |
02.11.2010 / Любимов Е.Б. |
Лекция 2
К числу наиболее простых и часто используемых методов уточнения корней относятся метод половинного деления (метод дихотомии или бисекции), метод хорд, метод Ньютона (метод касательных) и ряд других методов.
3.2.3. Метод дихотомии
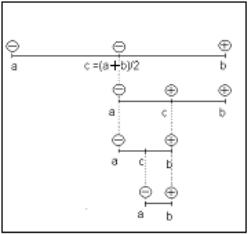
На каждом шаге итерации алгоритм метода дихотомии реализует уменьшение интервала неопределённости в два раза. На приводимой ниже диаграмме показаны первые шаги алгоритма. Знаки в кружочках соответствуют знакам при значениях функции, вычисляемым на каждом шаге.
Рис. 3.4. Диаграмма шагов алгоритма дихотомии
В начальный момент определены границы интервала неопределённости - точки a0B B и b0B ,B в которых значения функции имеют разные знаки. В рассматриваемом примере F(a0B )<0,B а F(b0B )>0B .
Определив точку с0B =(B a0B +bB 0B )B /2 в середине отрезка [a0B ,B b0B ]B вычисляем значение F(c0B )B . В рассматриваемом примере F(c0B )B <0. Поэтому определяем точку a1B B в точке с0B серединеB отрезка [a0B ,B b0B ],B определяя новый интервал [a1B ,B b1B ],B длина которого равна половине длины начального интервала.
На втором шаге итераций вновь определяем середину отрезка с1B иB вычисляем в ней значение функции. Если F(с1B )>0,B как это показано на рис. 3.4, переносим правый конец интервала точку b2B ,B в точку с1B ,B уменьшая тем самым интервал неопределённости ещё раз.
Повторяя шаги итерации, сокращаем интервал неопределённости до тех пор, пока не будет выполнено условие (3.7).
Окончательное решение определяет интервал [anB ,B bnB ],B длина которого меньше заданного значения δ. Значением корня уравнения следует считать одно из трёх чисел а, b или c. Из этих трёх точек
25 |
02.11.2010 / Любимов Е.Б. |
Лекция 2
выбирается точка, в которой значение функции F(а), F(b) или F(c) наименьшее по модулю.
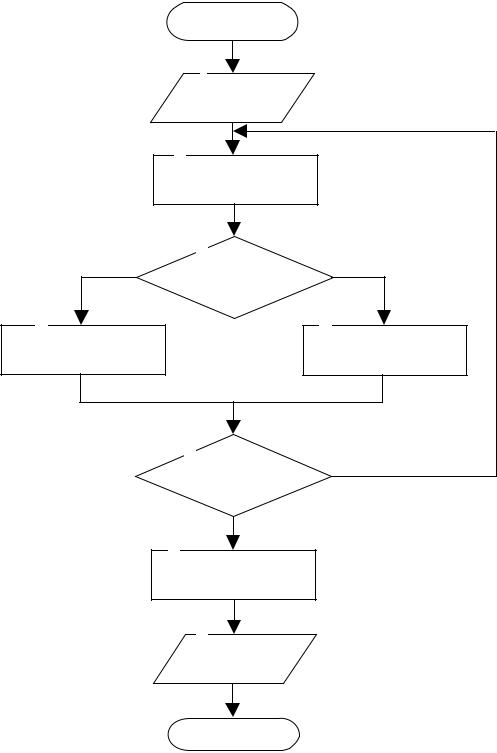
Один из возможных вариантов алгоритма, разработанный для программной реализации метода дихотомии, приведён на рис. 3.5.
|
Метод |
|
|
дихотомии |
|
||
1 |
Ввод |
|
|
параметров |
|
||
|
a, b,δ |
|
|
2 |
|
|
|
c:=(a+b)/2 |
|
||
3 |
|
да |
|
нет |
|
||
F(a)F(c)<0? |
|
||
4 |
|
5 |
|
a:=c |
|
b:=c |
|
6 |
|
да |
|
| b-a | > δ |
|||
|
|||
нет
7
с:=(a+b)/2 dx:=(b-a)/2
8 вывод
с,F(с),dx
конец
Рис. 3.5. Блок-схема алгоритма метода дихотомии
Перед обращением к функции, реализующей этот алгоритм, необходимо определить границы значения трёх параметров. Это границы начального интервала неопределённости [a, b], на которых
26 |
02.11.2010 / Любимов Е.Б. |
Лекция 2
выполнено условие (3.5), и значение параметра δ, задающее точность определения корня.
Вычисления продолжаются до тех пор пока длина интервала неопределённости (b-a) больше, чем значение, определяемое параметром δ (блок 6 рис. 3.5). При этом повторяются операции, реализуемые в блоках 2, 3, 4 или 5. Значение c определяет значение корня уравнения, а F(c) значение функции в найденном корне.
Цикл повторяется до тех пор, пока длина интервала [a; b] больше чем δ.
Как только значение |b-a| становится меньше, либо равно δ (блок 6 рис. 3.5), корень считается найденным. Его значением считается значение х, находящееся в середине последнего интервала [a; b] (блок 8 рис. 4). На экран выводится строка, содержащая значения корня х, значение функции F(х) в этой точке и параметр dx, определяющий возможную погрешность полученного решения.
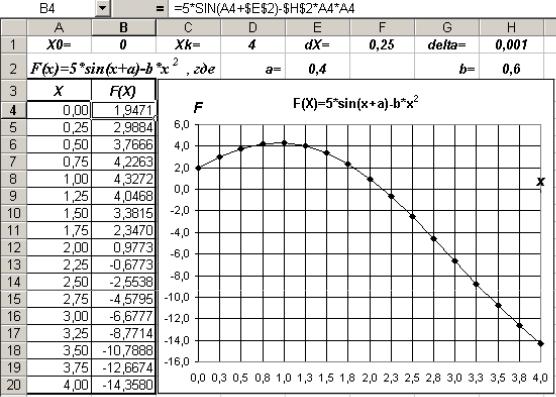
Рассмотрим реализацию метода дихотомии в среде программы Microsoft Excel на примере нахождения корня функции
F(x)=5*sin(x+a)-b*x2P .P
Интервал, в пределах которого требуется найти корень функции F(x), задан граничными значениями аргумента Х0 = 0 и Xk = 4.
Рис. 3.6. Таблица значений и график функции F(x)=5*sin(x+a)-b*x2P P , полученные на этапе предварительного исследования функции
27 |
02.11.2010 / Любимов Е.Б. |
Лекция 2
Выполним предварительный анализ функции F(x), вычислив таблицу её значений в интервале определённом значениями Х0, Xk. Шаг изменения аргумента dX возьмём равным 0,25. Результаты предварительного анализа приведены на рис. 3.6.
Анализируя таблицу значений функции, мы видим, что искомое решение находится в пределах интервала значений аргумента х, определяемого границами [2,00; 2,25].
Требуемую точность решения, определим значением параметра
δ = 0,001.
Для удобства дальнейшей работы запишем реализацию функции F(x) на языке программирования Visual Basic (VB), включённом в среду программ Microsoft Office:
В меню Сервис выбираем команду Макрос ► и далее команду Редактор Visual Basic (или просто нажимаем клавиши Alt + F11).
При первом обращении к программе Microsoft Visual Basic в основном меню выполняем команду Insert. Для записи функций пользователя необходимо создать модуль, выполнив для этого в меню Insert команду Module.
После создания модуля повторно открываем меню Insert и выбираем в нём команду Procedure. В открывающемся при выполнении этой команды окне Add Procedure в поле ввода Name вводим имя создаваемой процедуры, а в групповом поле Type включаем кнопку переключателя Function.
Назовём создаваемую нами функцию Fsin.
В окне редактора Visual Basic открывается заготовка текста создаваемой функции, которую мы дополним необходимыми операторами. Окончательно текст этой функции будет иметь следующий вид:
Public Function Fsin(a, b, x) Fsin = 5 * Sin(x + a) - b * x ^ 2 End Function
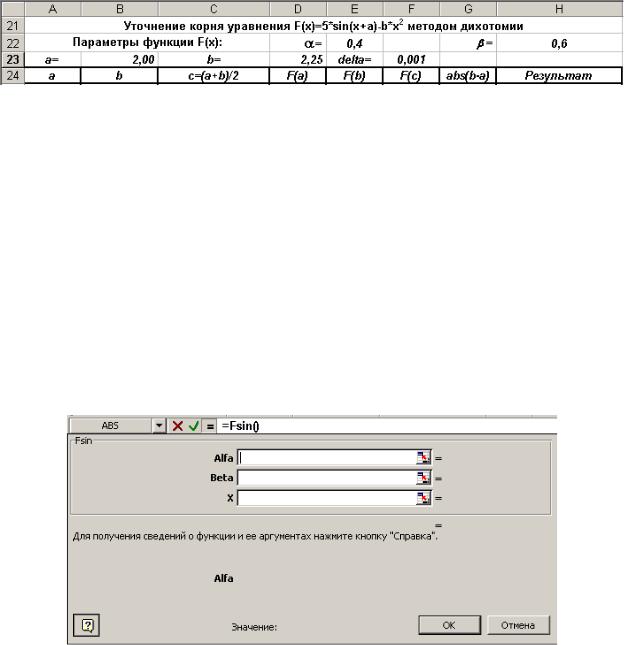
Создадим таблицу для уточнения корня уравнения
F(x)=5*sin(x+a)-b*x2P P в выделенном интервале [2,00; 2,25]. Формат её заголовка показан на рис. 3.7.
В ячейки 25-й строки записываются формулы, обеспечивающие формирование первой строки таблицы, в которой будет реализован метод дихотомии. Так в ячейку А25 записывается формула "=В23" - ссылка на ячейку, в которой записано значение аргумента Х0,
28 |
02.11.2010 / Любимов Е.Б. |
Лекция 2
соответствующее левой границе выделенного интервала неопределённости. В ячейку В25 записывается формула "=D23" - ссылка на ячейку, в которую записано значение правой границы выделенного интервала неопределённости.
Рис. 3.7. Заголовок таблицы для реализации алгоритма метода дихотомии
В ячейку С25 записывается формула, по которой вычисляется значение аргумента Х, определяющее срединную точку интервала неопределённости:
=(А25+В25)/2
Формула, по которой вычисляется значение функции F(x) в точке а, определяющей левую границу выделенного интервала неопределённости записывается в ячейку D25.
Обращение к функции Fsin выполняется через мастер функций программы Microsoft Excel. Функция Fsin выбирается из категории функций определённых пользователем.
На рис. 8 показано окно второго шага мастера функций, вызываемого при формировании обращения к функции Fsin.
Рис. 8. Окно второго шага мастера функций для функции Fsin()
В поле ввода Alfa этого окна записывается абсолютная ссылка $E$22 на ячейку Е22, в которую записано значение параметра функции α.
В поле ввода Beta записывается абсолютная ссылка $H$22 на ячейку H22, хранящую значение параметра функции β. В поле ввода X записывается относительная ссылка A25 на ячейку таблицы, в
29 |
02.11.2010 / Любимов Е.Б. |
