
Тема_5_Inf-2_МНК
.pdf
Лекция 5. Метод наименьших квадратов 5.1. Введение
Для получения аналитической зависимости, аппроксимирующей таблицу значений, полученную в результате некоторых измерений, можно применить один из методов интерполяции. В результате этого будет получена аналитическая функция
f = F(Х), |
(1) |
значения которой в точках х1, х2, …, xn будут совпадать с соответствующими значениями Yi (i=1,2,…,n) таблично заданной функции. Однако совпадение полученных значений в узловых точках таблицы не всегда обеспечивает совпадение поведения интерполирующей функции и реального физического процесса [1, 2]. В случаях, когда значения функции, записанные в таблицу, получены экспериментально, они, как правило, несут в себе некоторую измерительную погрешность. По этой причине в построении аналитической функции, аппроксимирующей реальную физическую зависимость необходимо учитывать характер исследуемого процесса.
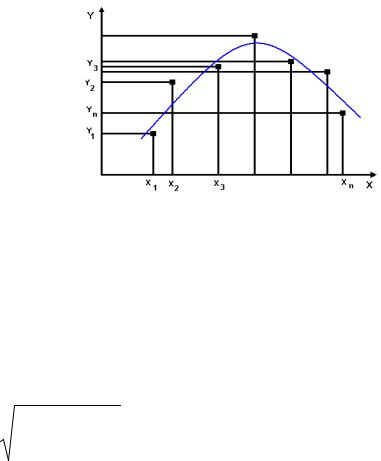
Ниже рассматривается пример обработки таблицы, полученной в результате проведённых в эксперименте измерений.
Рис.1 Таблица и диаграмма значений, полученных по результатам выполненных измерений
Функцию, определяемую формулой (1), часто называют
эмпирической формулой или уравнением регрессии Y на x, а функция
F(Х) - аппроксимирующей функцией (от латинского approximo - приближаюсь).
Близость вычисляемых значений аппроксимирующей функции F(Хi ) к табличным значениям аппроксимируемой функции Y(Xi ) обеспечивается выбором критерия, соответствующего алгоритму аппроксимации.
1
Одним из распространенных в |
|
|
|
|
|
инженерной практике методов |
|
|
|
|
|
получения аппроксимирующих |
|
|
|
|
|
зависимостей является |
|
|
|
|
|
графоаналитический метод. В этом |
|
|
|
|
|
методе по таблице, полученной в |
|
|
|
|
|
результате экспериментальных |
|
|
|
|
|
исследований, строится точечный |
|
|
|
|
|
график, а затем проводится плавная |
|
|
|
|
|
кривая наилучшим образом отражающая |
Рис. 2 |
|
|
||
характер точечной зависимости (рис. 2). |
|
|
|
||
Математические |
методы |
построения |
такого |
рода |
|
аппроксимирующих |
функций |
основываются |
на |
построении |
|
аналитических функций, для которых "расстояние" от заданной табличной функции минимально.
Расстояние между двумя множествами точек Yi |
и f |
i ( i = |
1,n |
) |
обычно |
определяется по формуле суммарного квадратичного отклонения |
|
||||
n |
|
||||
∑(Yi − fi )2 , |
(2) |
||||
i=1 |
|
||||
где Yi, значения функции, полученные экспериментально, а fi , вычисленные по формуле (1) значения аппроксимирующей аналитической функции.
Таким образом, задача нахождения аппроксимирующей функции формулируется следующим образом: для таблично заданной функции Y(xi) необходимо определить аналитическую функцию F(x), обеспечивающую минимальное расстояние (2) между этими функциями.
Для решения этой задачи используется метод, называемый методом наименьших квадратов (МНК), а задача называется задачей построения аппроксимирующей функции методом наименьших
квадратов.
В качестве аппроксимирующих функций в зависимости от характера точечного графика исходной функции y(xi) используются следующие функции [4]:
2

Таблица 1. Функции, наиболее часто используемые для аппроксимации табличных функций
1)f=ax+b
2)f=ax2+bx+c
3)f=axm
4)f=a·emx
5) f = |
1 |
|
ax +b |
||
|
6)f=a ln(x)+b
7)f = a 1x +b
8)f = axx+b
линейная регрессия; квадратичная регрессия;
геометрическая регрессия (степенная функция) показательная функция;
дробно-линейная функция; логарифмическая функция; гиперболическая функция;
дробно-рациональная функция.
В этих формулах коэффициенты a, b, c, m являются параметрами, значения которых должны обеспечивать минимум расстояния (суммарного квадратичного отклонения), определяемого по формуле (2).
Сравнение расстояний, определённых для разных аналитических аппроксимирующих функций, позволяет выбрать вид наилучшей аппроксимации для каждой конкретной таблично заданной функции.
После выбора типа функции f, решается задача оптимизации целевой (оптимизируемой) функцией которой является функция (2).
Выводы.
Подводя итоги вышесказанному, сделаем следующие выводы.
1.В зависимости от выбранного критерия для построения аппроксимирующих функций используются два класса методов:
-методы интерполяции, в которых критерием близости табличной и аппроксимирующей функции является точное совпадение их значений в узловых точках и
-методы аппроксимации, в которых критерием является
минимизация "расстояния" между заданной и аппроксимирующей функциями в узлах таблицы.
2.Выбор наилучшей аппроксимирующей функции для каждой конкретной табличной функции осуществляется путём сравнения "расстояний" между аппроксимирующими функциями и табличной функцией
3

5.2. Вычислениекоэффициентовфункциилинейнойрегрессии
5.2.1. Выводформулдляопределениякоэффициентовуравнения линейнойрегрессии
Функции линейной регрессии (линейная аппроксимирующая функция) является простейшей математической моделью, используемой для изучения различных процессов. Она записывается в виде
F(x,a,b)=a*x+b . |
(3) |
В этой функции x определяется значениями некоторой независимой переменной, определяющей поведение исследуемой функции, a и b - параметры, определяющие конкретную реализацию математической модели.
Оценка точности аппроксимации обычно выполняется либо по значению суммарного квадратичного отклонения (2), либо по значению среднего квадратичного отклонения (стандартного отклонения), вычисляемого по формуле
|
1 |
n |
− fi )2 . |
|
σ = |
∑(Yi |
(4) |
||
|
n |
i=1 |
|
|
Эта формула является осреднённым аналогом оценки расстояния между двумя множествами точек, определяемого по формуле (1).
Найдём частные производные функции линейной регрессии (3) по
параметрам: |
∂F |
= x , |
∂F |
= 1. |
(5) |
|
|||||
|
∂a |
∂b |
|||
|
|
|
|
Запишем функцию для определения суммарного квадратичного отклонения функции (1) от табличной функции с результатами измерений:
|
∑n [Yi − F( xi ,a,b )]2 =Φ( a,b ) |
(6) |
|
|
i =1 |
|
|
Найдём частные производные функции (6) по параметрам a и b и |
|||
приравняем их нулю: |
|
|
|
∂Φ |
= 2 ∑n ( yi − ax i −b )( −xi ) = 0 |
|
|
∂a |
i =1 |
(7) |
|
|
|||
∂Φ |
= −2 ∑n ( yi − ax i −b ) = 0 |
||
|
|||
∂b |
i =1 |
|
|
|
|
||
4
Из (7) получим (сумма во всех приводимых ниже формулах берётся для значений параметра i изменяющихся от 1 до n):
∑ xi yi − a ∑ xi2 − b ∑ xi |
= 0 |
∑ yi − a ∑ xi − nb = 0 |
(8) |
|
Введём обозначения:
S x |
= ∑n |
x i ; |
S |
|
i =1 |
|
|
||
S xy |
= ∑n |
x i y i ; |
S |
|
|
i =1 |
|
|
|
y |
|
= ∑n |
y i , |
|
|
|
i =1 |
|
(9) |
x |
2 |
= ∑n |
x i2 . |
|
|
i =1 |
|
|
и окончательно получим систему двух уравнений:
a S 2 |
+ b S x = S xy |
, |
||||||||||||
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
(10) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a Sx |
|
+ b n = S y . |
|
|||||||||||
Решение этой системы записывается в виде |
||||||||||||||
|
|
S |
|
− |
1 |
S |
S |
|
|
|
||||
xy |
|
|
y |
|
||||||||||
a = |
|
|
|
|
n x |
|
|
|||||||
S 2 |
− |
1 |
S 2 |
|
|
(11) |
||||||||
|
|
|
|
|||||||||||
|
|
|
||||||||||||
|
|
|
|
x |
|
|
|
n |
x |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
b = |
1 |
|
( Sy −a Sx ) |
|
||||||||||
|
|
|||||||||||||
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
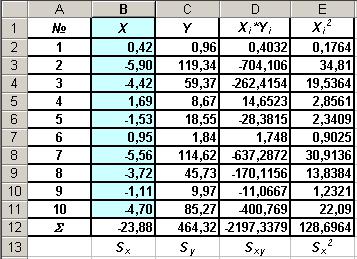
Вычисление значений сумм
(9) легко выполняется в среде программы Excel, как показано на рис. 3.
На основании этой таблицы система линейных алгебраических уравнений для определения значений параметров a и b может быть записана в виде:
128,6964 a - 23,88 b = -2197,3379
-23,88 a + 10 b |
= 464,32 |
(12) |
|
Рис. 3. Таблица результатов измерения и их обработки
Значения коэффициентов a и b, вычисленные по формулам (11) приведены на рис. 4.
5

Рис. 4. Коэффициенты уравнения линейной регрессии, вычисленные для значений функции, приведённой в таблице рис. 3
Формулы, соответствующие формулам (11) записаны в ячейки С15 и Е15 листа Excel. В ячейку С15 записана формула
=(D12-B12*C12/A11)/(E12-B12^2/A11)
В ячейку Е15 записана формула
=(C12-C15*B12)/A11
В этих формулах использованы ссылки на ячейки таблицы Excel, содержащие:
-в D12 ссылка на сумма Sхy ,
-в B12 ссылка на сумму Sх,
-в C12 ссылка на сумму Sх,
-в E12 ссылка на сумму Sх2,
-в A11 ссылка на значение n,
-в C15 ссылка на значение параметра а.
5.2.2.Определения коэффициентов уравнения линейной регрессии решениемсистемылинейныхалгебраическихуравнений
Правильность полученного решения может быть подтверждена решением системы уравнений (12) как системы линейных алгебраических уравнений (см. [3]). Для этого в ячейках таблицы сформируем матрицу коэффициентов левых частей уравнений и вектор правых частей уравнений, соответствующую (10). В формулах, записанных в ячейки таблицы Excel, используются ссылки на ячейки таблицы, приведённой на рис. 3.
Рис. 5. Фрагмент таблицы Excel, отображающий формулы для решения системы линейных уравнений (10), (12)
Результат, полученный при выполнении проверки, приведён на рис. 6
6

Рис.6. Фрагмент таблицы Excel, отображающий результаты решения системы линейных уравнений (12)
Значения параметров a и b, вычисленные в этом варианте решения, совпадают со значениями, полученными по формулам (11), что подтверждает правильность полученного решения.
В программе Microsoft Excel имеются специальные инструментальные средства, позволяющие определять для исследуемых табличных функций аппроксимирующие функции нескольких типов из числа перечисленных в таблице 1.
Ктаким средствам относятся:
-функции "Наклон", "Отрезок",
-инструмент "Поиск решения", доступный из меню "Сервис",
-инструмент "Добавить линию тренда", доступный из меню
"Диаграмма".
Ниже рассматривается методика использования этих инструментальных средств программы Excel.
5.2.3.Использование функций "Наклон", "Отрезок" для определения коэффициентов функции линейной регрессии
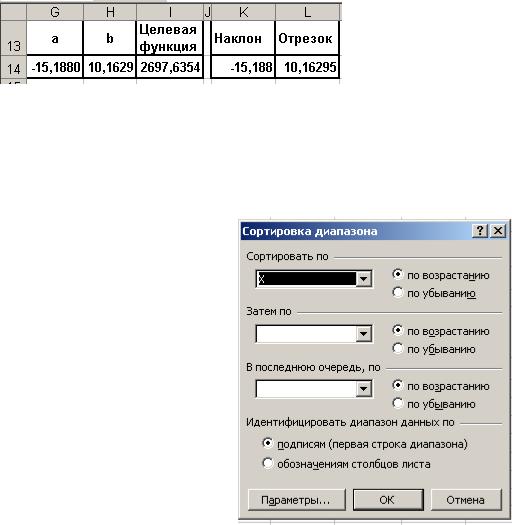
В комплекс системных функций программы Excel включены функции, позволяющие получить значения параметров, определяющих уравнение линейной регрессии (3). Функция Наклон обеспечивает вычисление коэффициента a уравнения (3), а функция Отрезок - вычисление значения коэффициента b.
Так, записав в двух соседних ячейках листа программы Excel, обращения к функциям
=НАКЛОН(H2:H11;G2:G11)
и
=ОТРЕЗОК(H2:H11;G2:G11)
получим в этих ячейках значения -15,1880 и 10,16295 совпадающие со значениями коэффициентов a и b, полученными методами, описанными выше.
7
5.2.4. Инструментальное средство "Поискрешения"
Инструментальное средство "Поиск решения" реализует в среде программы Excel алгоритм оптимизации математической модели, выбранной в качестве описания некоторого реального процесса, определяемого табличной функцией.
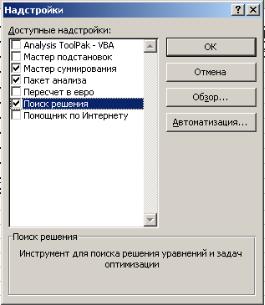
Для того чтобы сделать доступной инструмент "Поиск решения" следует в меню "Сервис" программы Excel выбрать команду "Надстройки...". В открывающемся при этом диалоговом окне
"Надстройки" в поле "Доступные надстройки" включить флажок
"Поиск решения" и нажать кнопку ОК. (см. рис. 7)
Рис. 7. Диалоговое окно "Надстройки"
Рассмотрим простейший пример использования инструментального средства "Поиск решения" для нахождения коэффициентов уравнения линейной регрессии (3) по данным таблицы, приведённой на рис. 1.
В этом решении коэффициенты a и b подбираются таким образом, чтобы минимизировать значение целевой функции (6), расстояние между исследуемой табличной функцией Y и функцией линейной регрессии F(x,a,b)= ax+b.
Для решения этой задачи (см. рис. 8), имея заполненную таблицу:
-столбец значений аргумента X ячейки G2:G11 и
-столбец значений функции Y ячейки Н2:Н11, выполняем следующие действия.
1.Выбираем ячейки G14 и Н14 для записи вычисляемых значений a и b.
2.Ещё одну ячейку I14 выберем для записи формулы, определяющей значение функции (6), минимизируемой при определении значений
8

коэффициентов a и b функции F(x,a,b)=ax+b. Эта формула в рассматриваемом примере имеет вид:
=СУММКВ(H2:H11-G14*G2:G11-H14) (13)
здесь H2:H11- диапазон ячеек, отведённых для значений функции Y;
Рис. 8. Окно надстройки "Поиск решения"
G14 - ячейка, выделенная для значения параметра a ;
G2:G11- диапазон ячеек, отведённых для массива значений функции X; H14 - ячейка, выделенная для значения параметра b.
Для выполнения вычислений по формуле, введённой в ячейку I14, её ввод завершается нажатием комбинации клавиш
<Ctrl>+<Shift>+<Enter>.
3.В меню "Сервис" выбираем команду "Поиск решения...". В открывающемся окне "Поиск решения" (см. рис. 8):
-в поле ввода "Установить целевую ячейку:" вводим абсолютную ссылку на ячейку таблицы I14, в которую ранее записали формулу (13);
-в поле переключателей "Равной:" включаем переключатель
"минимальному значению";
9
-в поле ввода "Изменяя ячейки" определяем диапазон ячеек G14:Н14, отведённых для вычисления значений коэффициентов a и b функции линейной регрессии.
4.Выполнив все вышеперечисленные действия, нажимаем кнопку "Выполнить" в окне "Поиск решения". Получаемые при этом в ячейках G14 и Н14 значения параметров a и b, совпадают со значениями этих параметров, полученными ранее при использовании других методов решения.
Рис. 9. Результаты выполнения "Поиска решения" и функций "Наклон" и "Отрезок"
5.2.5.Построениелиниитренда
1.Упорядочим таблицу функции F(x), приведённую на рис. 1 по возрастанию значений аргумента Х. Для этого:
-выделим столбцы со значениями аргумента Х и исходными значениями табличной функции Y;
-в меню "Данные" выбираем команду "Сортировка..." и в открывающемся окне "Сортировка диапазона" (см.
рис. 10) проверяем состояние переключателя в поле "Сортировать по", устанавливая его в режим "по возрастанию".
-нажимаем кнопку "ОК". Результат выполненной сортировки показан на рис. 11.
Рис. 10. Окно команды
"Сортировка..."
2. В первую ячейку следующего столбца таблицы введём формулу |
|
=$G$14*O2+$H$14 |
(14) |
где $G$14 и $H$14ссылки на ячейки, в которых находятся значения параметров a и b функции линейной регрессии (см. рис. 9), а в ячейке O2 находится первое значение аргумента X.
3.Протянем эту формулу по столбцу для всех значений Х.
4.Построим точечные графики функций Y и F(X).
10
