
Числ_мет_реш_нелин_ур-ний(ч1)
.pdfМетоды решения нелинейных уравнений
Численные методы решения нелинейных уравнений (Часть 1)
Общий подход к решению нелинейных уравнений
Решение нелинейных уравнений обычно осуществляется в 2 этапа:
1 этап – отделение корней состоит в выделении на заданном интервале изменения аргумента [X0, Xk] подынтервалов, содержащих только один корень. Для отделения корней обычно выполняется вычисление таблицы значений функции и (или) построение её графика;
2 этап - уточнение корней выполняется на каждом промежутке, содержащем один корень, выделенном на первом этапе исследования поведения функции. Для уточнения значения корня выбирается один из численных методов. Наиболее часто используются метод половинного деления (дихотомии), метод хорд, метод касательных (Ньютона) и др.
Предварительный анализ функции
Рассмотрим процедуру выполнения первого этапа на примере
проведения предварительного анализа функции |
|
Y (x) ax3 bx2 cx d |
(1) |
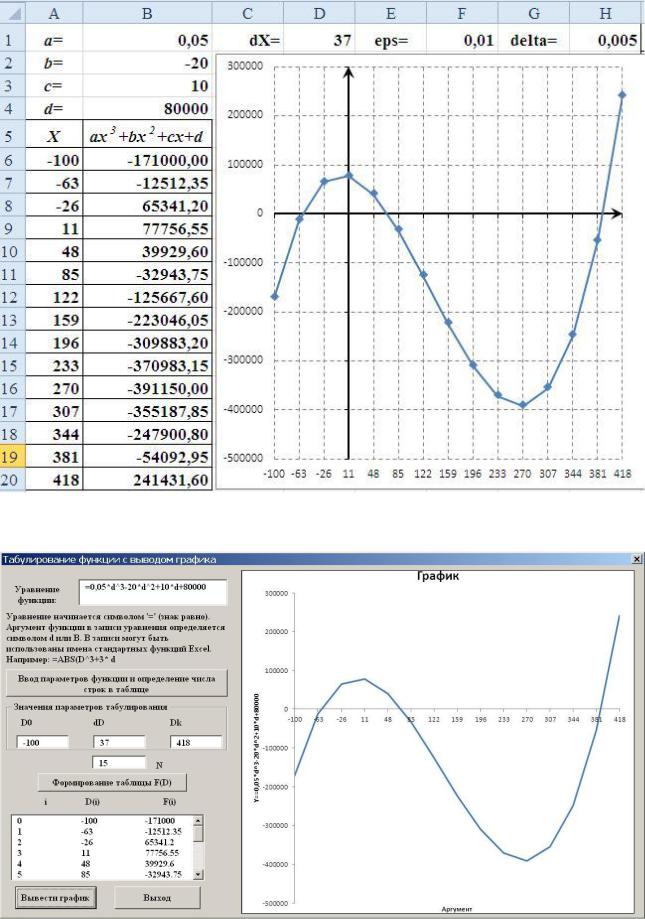
Определим значения параметров, входящих в описание функции: a=0,05; b=-20; c=10; d=80000.
Используя программу MS Excel, можно вычислить таблицу значений и построить график функции (см. рис. 1). Аналогичные результаты можно получить, используя приложение "Табулирование функции с выводом графика", разработанное в предыдущей лабораторной работе (см. рис. 2).
На полученных графиках мы можем определить три области, в пределах которых находятся корни функции (1). Это интервалы:
1-й корень Є(-63; -26): Y(-63) = -12512,15; Y(-26) = 65341,2 2-й корень Є(48; 85): Y(48) = 39929,6; Y(85) = -32943,75 и 3-й корень Є(381; 418): Y(381) = -54092,95; Y(418) =241431,6.
Известно, что полином третьей степени имеет либо один, либо три вещественных корня. Поэтому проведённый предварительный анализ позволил определить области отделения для всех корней функции (1).
1 |
Любимов Е.Б. |
Методы решения нелинейных уравнений
Рис. 1. Результат табулирования функции и построения графика в среде программы MS Excel.
Рис. 2. Результаты выполнения приложения "Табулирование функции с выводом графика"
2 |
Любимов Е.Б. |
Методы решения нелинейных уравнений
Рассмотрим процесс уточнения наименьшего из корней функции Y(x) методом дихотомии.
Признаком того, что корень функции находится в пределах
заданного интервала является выполнение условия |
|
Y(ai)*Y(bi) <=0, |
(2) |
где ai и bi определяют границы интервала неопределённости на i-ой итерации процесса уточнения значения корня.
Значение корня можно считать найденым, если одновременно
выполняются два условия: |
|
| Y(x) | , |
(3) |
и |
|
|(xi+1-xi)| . |
(4) |
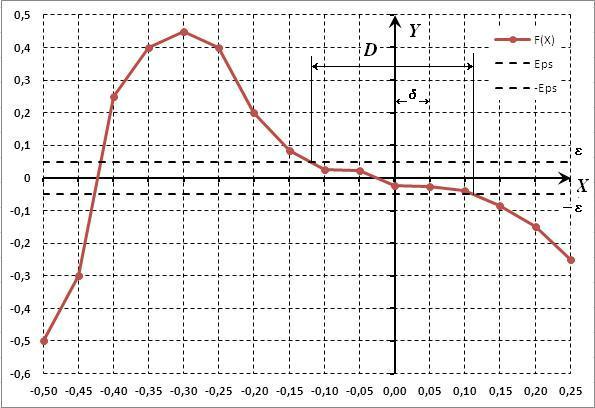
Обычно для окончания итерационного процесса уточнения корня считается достаточным выполнение условия (3), но, как показано на рис. 3, возможны ситуации, в которых это условие выполняется на слишком широком интервале [ai,bi].
Рис. 3. Пример функции с "размытым" корнем
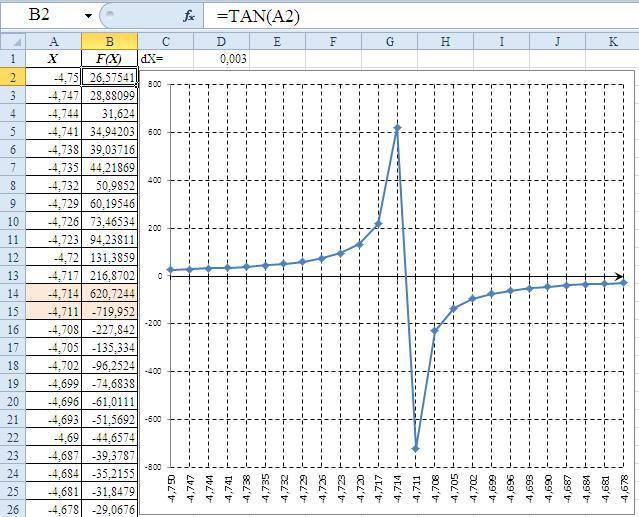
Исследуя поведение функций, следует помнить об ещё одном возможном варианте поведения функции, а именно о существовании в некоторых функциях точек, называемых точками разрыва.
Пример графика такой функции приведён на рис. 4.
3 |
Любимов Е.Б. |
Методы решения нелинейных уравнений
Рис. 4. Функция с разрывом, не имеющая корня на этом интервале
Пример реализации алгоритма уточнения корня методом дихотомии
Рассмотрим пример реализации алгоритма метода дихотомии. В качестве исследуемой функции возьмём для выполнения вычислений более простую, чем (1), функцию
Y(X) = X3 - 5X + 3 |
(5) |
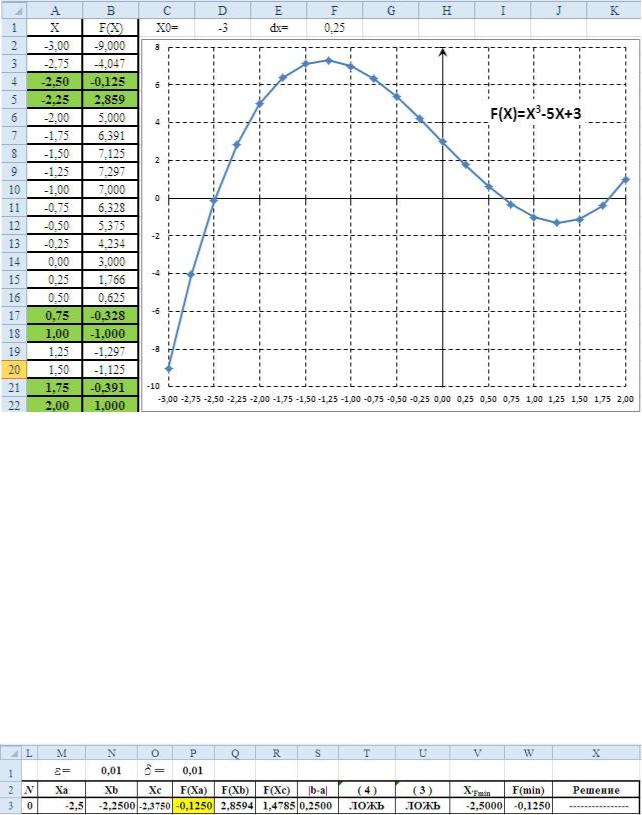
На рис. 5 приведены таблица значений и график этой функции.
Построив таблицу и график этой функции определим три интервала [ai, bi], в пределах которых находятся корни. Эти интервалы выделены в таблице:
[-2,5; -2,25], [0,75; 1,00] и [1,75; 2,00].
Зададим значения параметров используемых для определения критериев окончания итерационного процесса. Пусть = = 0,01.
4 |
Любимов Е.Б. |
Методы решения нелинейных уравнений
Рис. 5. Таблица значений и график функции Y(X) = X3 - 5X + 3
Для получения значений корней с требуемой точностью на каждом из выделенных интервалов необходимо использовать один из методов уточнения.
На приведённом на рис. 5 графике выделены три интервала нахождения корней:
[-2,5; -2,25], [0,75; 1,00] и [1,75; 2,00].
Рассмотрим пример уточнения наименьшего из корней функции
(5). Этот пример может быть выполнен методом ручных вычислений, либо оформлен в таблице Microsoft Excel.
Для выполнения вычислений оформим таблицу, в заголовке которой определим 12 столбцов (см. рис. 6).
Рис. 6. Заголовок и первая строка таблицы
Во второй строке таблицы Excel запишем наименования столбцов, показанные на рис. 6.
В столбцах третьей строки таблицы запишем значения аргумента функции в точках, определяющих начало, конец и
5 |
Любимов Е.Б. |
Методы решения нелинейных уравнений
середину интервала неопределённости (Ха, Xb и Xc - столбцы M, N, O). В ячейки трёх следующих столбцов (P, Q, R) записываются вычисленные значения функции (Y(Ха), Y(Xb) и Y(Xc)).
Вследующих 6-ти столбцах таблицы выполняются операции, обеспечивающие анализ параметров, определяющих окончание процедуры решения. Так в столбце S вычисляется длина интервала неопределённости | b - a | - расстояние между точками Xb и Xa.
Вдвух следующих столбцах T и U выполняется проверка условий (4) и (3). Результаты этих проверок логические значения {ИСТИНА} или {ЛОЖЬ} используются затем для определения
момента окончания итеративного процесса .
Встолбце V определяется значение аргумента Х, соответствующее точке Xa, Xb или Xc, в которой на данном шаге итераций значение функции Y(Х) имеет значение наименьшее из трёх. Значение функции в выбранной точке выводится в ячейку столбца W.
Вячейках столбца Х, записана функция, выполняющая проверку одновременного выполнения условий (3) и (4). При достижении конца итерационного процесса в ячейку столбца Х выводится сообщение с указанием достигнутой точки решения.
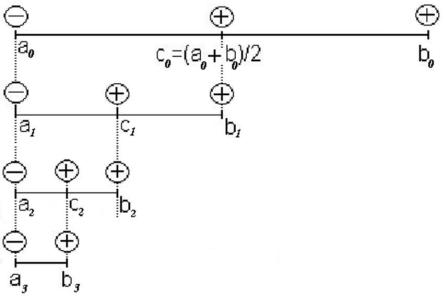
Метод дихотомии
Рис. 7 Пошаговая схема алгоритма дихотомии.
Перед выполнением первого шага определен интервал [a0, b0] и значения исследуемой функции на концах этого интервала, называемого начальным интервалом неопределённости корня функции F(x).
6 |
Любимов Е.Б. |

Методы решения нелинейных уравнений
Условие (2), определяющее наличие корня в интервале [a0, b0], на схеме рис. 7 отображается знаками функций на концах интервала. По формуле
c0=a0+(b0-a0)/2=(a0+b0)/2 |
(6) |
|
определяем координату точки с0, находящейся в середине отрезка [a0, b0], вычисляем значение функции F(с0).
Если F(а0) F(с0) <= 0, как это показано на рис. 7, то граница a1 остаётся в точке a0, а граница b1 переносится в точку c0, т.е. выполняются операции:
a1 := a0 и b1 := с0=(a0+b0)/2,
здесь обозначение ":=" определяет операцию и читается
"присвоить".
Значение с1 определяется как с1=(a1+b1)/2, после чего проверяется выполнение условия F(а1)F(с1)<=0. Если оно выполнено, то граница b2 определяется как значение с1, в случае же если условие F(а1)F(с1)<=0 не выполняется, то граница а2 переносится в точку с1, а граница b2 остаётся в точке b1.
Аналогично выполняются и следующие шаги.
Рассмотрим методику ручных вычислений, оформленную аналогично методике реализации алгоритма в программе Excel.
Выполняя ручные вычисления на первых шагах, можно не беспокоиться о проверке условий окончания до тех пор, пока вычисляемые значения функции значительно больше значения .
Совершая первый шаг алгоритма вычисляем значение аргумента в середине отрезка [a, b]: | b0- a0 | = 0,2500;
c0 = a0+(b0 - a0)/2 = (a0 + b0)/2= (-2,5+-2,25)/2=-2,3750.
Вычисляем значение
Y(-2,375)= 1,4785 Y(a)* Y(c) = -0,125*1,4785 < 0
переносим границу b в точку с, т.е. a1 =a0 =-2,5,
а b1 = с0=-2,3750. |
| b1- a1| = 0,1250; |
Находим новое значение
c1 = (a1 + b1)/2= (-2,5+-2,375)/2=-2,4375;Y(c1)=Y(-2,4375)=0,7053.
Y(a1)* Y(c1) = -0,125*0,7053 < 0 переносим границу b в точку
с, т.е. a2 =a1 ,а b2 = с1. | b2- a2| = 0,0625
c2 = (a2 + b2)/2=(-2,5+-2,4375)/2= -2,4688; Y(c2) =0,2974
Y(a2)* Y(c2) = -0,125*0,2974 <0 переносим границу b в точку
с, т.е. a3 =a2 ,а b3 = с2
7 |
Любимов Е.Б. |
Методы решения нелинейных уравнений
c3 = (a3+b3)/2=(-2,5+-2,4688)/2= -2,4844; F(c3) =0,0880
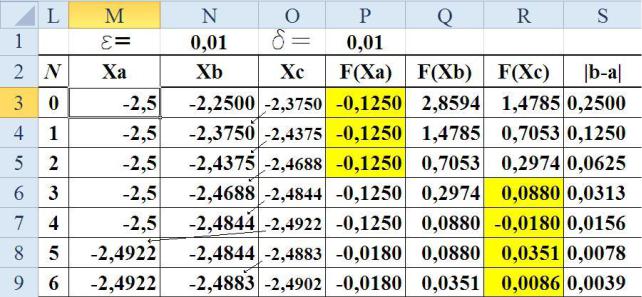
Оформим эти вычисления в таблицу и продолжим вычисления до получения решения с требуемой точностью.
Таблица 1. Результаты ручных вычислений
i |
ai |
bi |
ci |
Y(a) |
Y(c) |
Y(b) |
|b-a| |
0 |
-2,5 |
-2,25 |
-2,375 |
-0,1250 |
1,4785 |
2,8594 |
0,25 |
1 |
-2,5 |
-2,375 |
-2,4375 |
-0,1250 |
0,7053 |
1,4785 |
0,125 |
2 |
-2,5 |
-2,4375 |
-2,4688 |
-0,1250 |
0,2974 |
0,7053 |
0,0625 |
3 |
-2,5 |
-2,4688 |
-2,4844 |
-0,1250 |
0,0880 |
0,2974 |
0,0313 |
4 |
-2,5 |
-2,4844 |
-2,4922 |
-0,1250 |
-0,0180 |
0,0880 |
0,0156 |
5 |
-2,4922 |
-2,4844 |
-2,4883 |
-0,0180 |
0,0351 |
0,0880 |
0,0078 |
6 |
-2,4922 |
-2,4883 |
-2,4902 |
-0,0180 |
0,0086 |
0,0351 |
0,0039 |
Аналогичные результаты могут быть получены и оформлены в среде программы MS Excel, приводимыми на рис. 8.
Рис. 8. Аналог таблицы 1, формируемый при вычислениях в среде программы
MS Excel
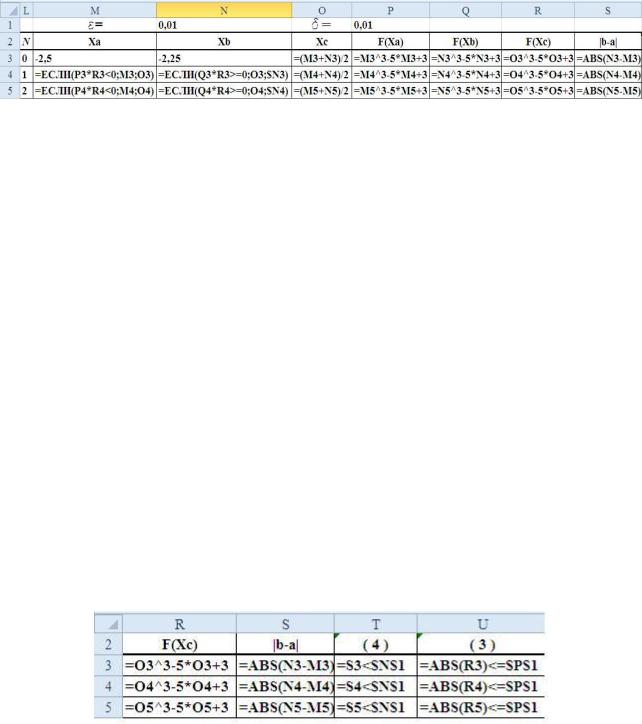
Для реализации этого процесса в среде программы MS Excel в ячейки таблицы следует записать формулы, позволяющие перейти от ручных вычислений к автоматизированному процессу (см. рис.9).
В ячейки 0-й строки таблицы вводим формулы, начиная с ячейки О3. Вид первых строк этой таблицы в режиме отображения формул приведён на рис. 9. - рис. 12.
8 |
Любимов Е.Б. |
Методы решения нелинейных уравнений
Рис. 9. Таблица формул столбцов, вычисляемых для определения границ интервалов, значений функций и длины интервала неопределённости
Для полной автоматизации алгоритма нахождения корня дополним столбцы вычислений столбцами анализа результатов. В столбцы T и U (см. рис. 10) введём формулы для проверки выполнения условий (4) и (3). В результате вычислений, выполняемых по этим формулам в ячейках этих столбцов формируются логические значения ИСТИНА, если условия выполнены, и ЛОЖЬ в противном случае.
Так в ячейки столбца Т записываем формулу "=S3<$N$1".
В этой формуле относительная ссылка S3 определяет текущее значение длины интервала | b - a |, которое сравнивается со значением константы , записанной в ячейку $N$1.
Аналогичная формула "=abs(R3)<=$P$1"записывается в ячейки столбца U. В этой формуле модуль текущего значения функции F(Xc) сравнивается со значением константы , записанной в ячейку $P$1.
Результатами вычислений по этим формулам, как уже отмечалось выше, являются логические (булевские) значения
ИСТИНА или ЛОЖЬ.
Рис. 10. Формулы, используемые для проверки выполнения условий (3) и (4)
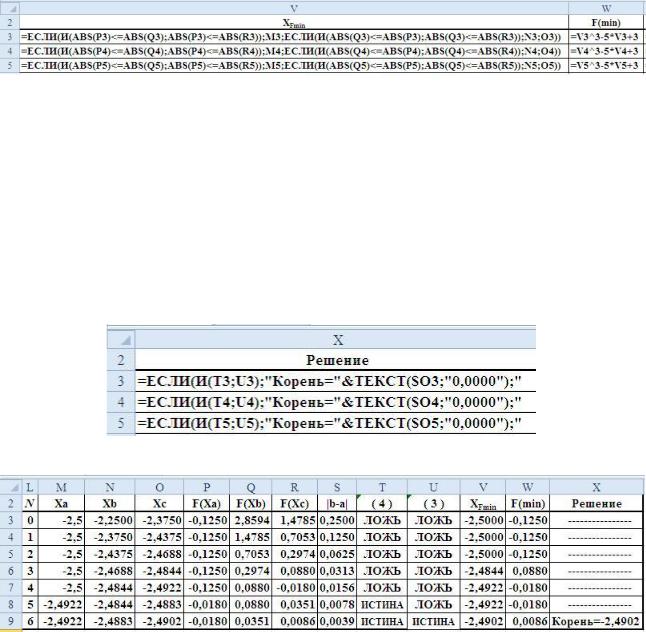
Формула, записываемая в ячейку столбца V (см. рис. 11),
=ЕСЛИ(И(ABS(P3)<=ABS(Q3);ABS(P3)<=ABS(R3));M3; ЕСЛИ(И(ABS(Q3)<=ABS(P3);ABS(Q3)<=ABS(R3));N3;O3))
используется для определения координаты точки с наименьшим значением исследуемой функции. Это значение используется для вычисления значения функции в ячейке столбца W.
9 |
Любимов Е.Б. |
Методы решения нелинейных уравнений
Рис. 11. Формул, обеспечивающие определение значения аргумента и соответствующего ему минимального значению функции
В ячейки последнего столбца таблицы Х (рис. 11) записывается формула
=ЕСЛИ(И(T3;U3);"Корень="&ТЕКСТ($O3;"0,0000");"---------------- |
"), |
|
которая обеспечивает вывод строки "---------------- |
", если корень ещё |
|
не найден, или сообщения |
|
|
"Корень="&Х,
если корень найден. Здесь Х - значение аргумента в точке корня.
Рис. 11. Формулы, вычисляемые для определения значения корня
Рис. 12. Полная таблица нахождения корня уравнения Y(X) = X3 - 5X + 3
Создание функции пользователя и её использование при решении нелинейного уравнения
Так как значения исследуемой функции вычисляются в нескольких столбцах таблицы, то более удобным вариантом записи алгоритма будет создание функции пользователя, реализующей вычисление значений Y(X).
Для этого в программе MS Excel перейдём в меню Разработчик, а затем на ПИ этого меню нажимаем кнопки Режим конструктора и Visual Basic. В меню окна MS VBA выбираем команду Insert. Если в файле программы ещё не были созданы
10 |
Любимов Е.Б. |
