
Шпора
.docx
В общем случае
сложного сопротивления
в стержне возникают все шесть видов
внутренних усилий одновременно. Эти
шесть усилий определяем, как обычно,
методом сечений и строим эпюры усилий.
Для определения положения опасных
точек в круглом
сечении
построим эпюры распределения напряжений.
Чтобы построить эпюру нормальных
напряжений, вызванных двумя изгибающими
моментами
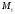 и
и
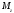 ,
определим направление суммарного
изгибающего момента. Поскольку для
круглого сечения любая ось является
главной, то в какой бы плоскости ни был
приложен изгибающий момент, он вызывает
плоский изгиб. Нейтральная линия в этом
случае перпендикулярна плоскости
изгиба, то есть совпадает с линией
действия вектора полного изгибающего
момента
,
определим направление суммарного
изгибающего момента. Поскольку для
круглого сечения любая ось является
главной, то в какой бы плоскости ни был
приложен изгибающий момент, он вызывает
плоский изгиб. Нейтральная линия в этом
случае перпендикулярна плоскости
изгиба, то есть совпадает с линией
действия вектора полного изгибающего
момента
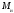 .
Кроме того, в сечении возникают
нормальные напряжения от продольной
силы N
и касательные напряжения от крутящего
момента
.
Кроме того, в сечении возникают
нормальные напряжения от продольной
силы N
и касательные напряжения от крутящего
момента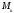 .
Для пластичных материалов – третья
теория прочности
.
Для пластичных материалов – третья
теория прочности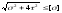 .
.
В
формулах
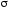 и
и
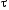 – напряжения в опасных точках.
– напряжения в опасных точках.
 ;, где
;, где
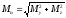 ;
;
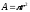 ;
;
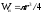 ;
;
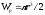 .
.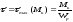
Косым изгибом называется такой изгиб, при котором вся нагрузка на балку действует в одной плоскости и эта плоскость не совпадает с плоскостями, в которых лежат главные центральные оси инерции сечения. При косом изгибе изогнутая ось представляет собой плоскую кривую и плоскость, в которой она расположена, не совпадает с плоскостью действия нагрузки. При пространственном изгибе нагрузка приложена в разных плоскостях деформированная ось является пространственной кривой.
При
косом или пространственном изгибе в
сечении стержня возникают четыре усилия:
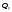 ,
,
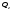 ,
,
 и
и
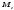 .
Нормальные напряжения в произвольной
точке сечения определяются по формуле,
полученной из при
.
Нормальные напряжения в произвольной
точке сечения определяются по формуле,
полученной из при
 ,
,
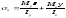 .
Касательные напряжения от поперечных
сил, если нельзя воспользоваться формулой
Журавского, допустимо не учитывать.
.
Касательные напряжения от поперечных
сил, если нельзя воспользоваться формулой
Журавского, допустимо не учитывать.
Определение положения опасных точек в стержне произвольного поперечного сечения производится по схеме, описанной ранее во вступительной части разд. 5. Поскольку в уравнении нейтральной линии
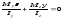 отсутствует
свободный член, то нейтральная линия
проходит через центр тяжести сечения
(рис. 5.5). Построив нейтральную линию
и эпюру нормальных напряжений, найдем
положение опасных точек. Допустим, что
напряжение в точке 1 больше, чем в точке
1
(это можно определить по масштабу, если
построить сечение и эпюру напряжений
в масштабе). Условие прочности в опасной
точке 1, которая находится в линейном
напряженном состоянии, записывается
так:
отсутствует
свободный член, то нейтральная линия
проходит через центр тяжести сечения
(рис. 5.5). Построив нейтральную линию
и эпюру нормальных напряжений, найдем
положение опасных точек. Допустим, что
напряжение в точке 1 больше, чем в точке
1
(это можно определить по масштабу, если
построить сечение и эпюру напряжений
в масштабе). Условие прочности в опасной
точке 1, которая находится в линейном
напряженном состоянии, записывается
так:
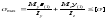 .
Значение
.
Значение
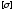 зависит от материала, из которого сделана
балка, и для хрупкого материала необходимо
учесть направление (растягивающее или
сжимающее)
зависит от материала, из которого сделана
балка, и для хрупкого материала необходимо
учесть направление (растягивающее или
сжимающее)
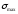 .
Для некоторых форм сечений, а именно
прямоугольника, двутавра и других
сечений, угловые точки которых находятся
в углах прямоугольника, нет необходимости
для записи условий прочности находить
положение опасных точек. Для таких
сечений положение опасных точек не
зависит от угла наклона нейтральной
линии, и опасные точки – это всегда
угловые точки сечения. Условие прочности
в этих точках записывается следующим
образом:
.
Для некоторых форм сечений, а именно
прямоугольника, двутавра и других
сечений, угловые точки которых находятся
в углах прямоугольника, нет необходимости
для записи условий прочности находить
положение опасных точек. Для таких
сечений положение опасных точек не
зависит от угла наклона нейтральной
линии, и опасные точки – это всегда
угловые точки сечения. Условие прочности
в этих точках записывается следующим
образом:
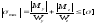
Сложный изгиб с растяжением (сжатием). Если на балку действуют и продольные и поперечные нагрузки, пересекающие ось бруса, то в общем случае в поперечных сечениях возникают изгибающие моменты Мz и Му в двух плоскостях, поперечные силы Qz и Qy, а также продольная сила N Таким образом, в этом случае будет сложный изгиб с растяжением или сжатием.
Нормальное напряжение в произвольной точке сечения
|
|
(10.54) |
Изгибающие моменты, продольную силу и координаты точки, в которой вычисляют напряжения, подставляют сюда с их знаками.
Пренебрегая касательными напряжениями от поперечных сил, можно считать, что напряженное состояние в опасной точке линейно. Следовательно, условие прочности имеет простейший вид:
|
|
(10.55) |
Если сечение имеет две оси симметрии и выступающие углы, то опасной будет одна из угловых точек. Напряжения в ней определяют по формуле (10.54) или так:
|
|
(10.56) |
Знаки в этой формуле комбинируют по смыслу или на основе сопоставления с формулой (10.54).
В случае плоского изгиба в главной плоскости уОх с растяжением (сжатием) трехчленная формула превращается в двучленную:
|
|
(10.57) |
Эти формулы применяют при расчете на прочность плоских рам и арок малой кривизны. Опасными в этом случае являются те сечения, где действует наибольший изгибающий момент
При расчете брусьев с поперечным сечением произвольной формы для определения опасной точки сечения необходимо, прежде всего, установить положение нейтральной линии.
Внецентренное
растяжение-сжатие
– такой вид деформации, при котором
стержень загружен растягивающими и
(или) сжимающими силами, приложенными
вне центра тяжести поперечного сечения.
При внецентренном растяжении-сжатии
стержней в стержне возникают три
внутренних усилия: продольная сила (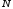 )
и два изгибающих момента (
)
и два изгибающих момента (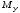 и
и
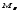 ).
Предполагается, что стержень имеет
большую жесткость, т. е. его длина не
слишком велика по сравнению с размерам
поперечного сечения.
).
Предполагается, что стержень имеет
большую жесткость, т. е. его длина не
слишком велика по сравнению с размерам
поперечного сечения.
От найденных усилий в стержне возникают только нормальные напряжения, которые определяются по формуле (5.1). Для проверки прочности стержня необходимо найти максимальные напряжения. Определение этих напряжений производится по схеме, описанной ранее, т. е.:
-
строим нейтральную линию по уравнению
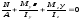 .
.
-
находим положение опасных точек;
-
подставляя в
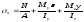 координаты опасных точек, вычисляем
напряжения в этих точках;
координаты опасных точек, вычисляем
напряжения в этих точках; -
для проверки прочности сравниваем максимальные напряжения с допускаемыми.
Используя
уравнение нейтральной линии, найдем
отрезки
 ,
,
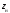 ,
отсекаемые нейтральной линией на осях
координат (рис. 5.10),
,
отсекаемые нейтральной линией на осях
координат (рис. 5.10),
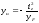 ;
; 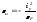 .
(5.12)
.
(5.12)
-
нейтральная линия всегда расположена в квадранте, противоположном тому, в котором находится полюс (см. рис. 5.10);
-
если полюс находится на одной из главных осей, то нейтральная линия перпендикулярна этой оси;
-
если полюс приближается к центру тяжести сечения, то нейтральная линия удаляется от него;
-
если полюс движется по прямой линии, то нейтральная линия поворачивается вокруг неподвижной точки.
Из предпоследней закономерности следует, что если сила приложена достаточно близко к центру тяжести, то нейтральная линия удаляется так далеко, что нигде не пересекает сечение. Это означает, что напряжения во всем сечении будут иметь один знак. Следовательно, существует такая область вокруг центра тяжести, которая обладает следующим свойством: если внутри этой области или на ее контуре приложить силу (растягивающую или сжимающую), то во всем сечении будут возникать напряжения одного знака. Такая область называется ядром сечения.
Расчет
вала на изгиб с кручением.
Коленчатый вал является плоской рамой,
испытывающей действие пространственных
циклических нагрузок, в которой возможно
усталостное разрушение, поэтому, кроме
расчета на статические нагрузки,
требуется учет влияния на напряжения
динамического действия нагрузок.
Известно, что под действием длительных,
циклически меняющихся нагрузок материалы
конструкций обнаруживают значительное
понижение прочности. Это явление носит
название усталости
материала.
Способность материала сопротивляться
усталостному разрушению называют
выносливостью.
Важной характеристикой материала
является предел выносливости, определяемый
экспериментально. Один из способов
расчета на усталостную прочность
сводится к определению действительного
коэффициента запаса усталостной
прочности
 и сравнению его с нормируемым коэффициентом
запаса n.
В данном расчете примем
и сравнению его с нормируемым коэффициентом
запаса n.
В данном расчете примем
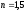 .
Условием усталостной прочности является
условие
.
Условием усталостной прочности является
условие
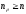 .
)Для "балочного"
напряженного состояния, которое имеет
место в опасных точках коленчатого
вала, коэффициент запаса усталостной
прочности находится по формуле Гафа и
Полларда
.
)Для "балочного"
напряженного состояния, которое имеет
место в опасных точках коленчатого
вала, коэффициент запаса усталостной
прочности находится по формуле Гафа и
Полларда
 ,
(5.52)
,
(5.52)
где
 – запас прочности по нормальным
напряжениям в предположении, что
касательные напряжения равны нулю;
– запас прочности по нормальным
напряжениям в предположении, что
касательные напряжения равны нулю;
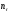 – запас прочности по касательным
напряжениям, когда
– запас прочности по касательным
напряжениям, когда
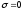 .
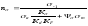
Коэффициенты
.
Коэффициенты
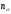 и
и
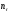 определяются следующим образом:
определяются следующим образом:
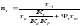
 ;
;
В
формулах (5.53), (5.54)
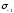 и
и
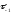 – пределы выносливости при изгибе и
кручении для симметричного цикла;
– пределы выносливости при изгибе и
кручении для симметричного цикла;
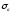 ,
,
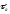 – амплитудные значения цикла напряжений
при изгибе и кручении;
– амплитудные значения цикла напряжений
при изгибе и кручении;
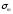 ,
,
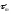 – средние напряжения цикла при изгибе
и кручении. Остальные величины, входящие
в формулы (5.53), (5.54), являются эмпирическими
коэффициентами, учитывающими:
– средние напряжения цикла при изгибе
и кручении. Остальные величины, входящие
в формулы (5.53), (5.54), являются эмпирическими
коэффициентами, учитывающими:
-
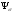 ,
,
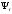 – влияние среднего напряжения на
величину сопротивления усталости;
– влияние среднего напряжения на
величину сопротивления усталости; -
 ,
,
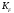 – масштабный фактор и степень
шероховатости поверхности;
– масштабный фактор и степень
шероховатости поверхности; -
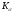 ,
,
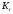 – влияние концентрации напряжений на
сопротивление усталости.
– влияние концентрации напряжений на
сопротивление усталости.
Метод Максвелла – Мора определения перемещений является универсальным методом, справедливым для любых стержневых систем. Чтобы понять сущность метода Максвелла – Мора, введем понятия обобщенной силы и обобщенного перемещения. Обобщенной силой называется любое однопараметрическое силовое воздействие: это может быть и сосредоточенная сила, и сосредоточенный момент, и распределенная нагрузка, и группа сил, связанных между собой. Обобщенным перемещением, соответствующим заданной обобщенной силе, называется то перемещение, на котором обобщенная сила совершает работу. Приведем два самых важных для практики примера. Запишем приближенную формулу Максвелла – Мора, которая используется для определения перемещений в изгибаемых плоских стержневых системах и не учитывает влияния на перемещения продольной и поперечной сил:
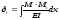 .
(4.21) В этой формуле
.
(4.21) В этой формуле
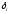 – искомое обобщенное перемещение (это
может быть и прогиб, и угол поворота
любого сечения); М
– изгибающий момент от заданной нагрузки;
Мi
– изгибающий
момент, вызванный единичной обобщенной
силой, соответствующей искомому
перемещению; EI
– жесткость стержня при изгибе
(произведение модуля упругости на момент
инерции). Интегрирование в формуле
Максвелла – Мора ведется по длинам всех
стержней конструкции (по длинам всех
участков балки).
– искомое обобщенное перемещение (это
может быть и прогиб, и угол поворота
любого сечения); М
– изгибающий момент от заданной нагрузки;
Мi
– изгибающий
момент, вызванный единичной обобщенной
силой, соответствующей искомому
перемещению; EI
– жесткость стержня при изгибе
(произведение модуля упругости на момент
инерции). Интегрирование в формуле
Максвелла – Мора ведется по длинам всех
стержней конструкции (по длинам всех
участков балки).
Таким образом, чтобы воспользоваться формулой Максвелла – Мора, надо:
-
определить изгибающий момент на каждом участке от заданной нагрузки;
-
освободить конструкцию от заданной нагрузки и загрузить ее единичной обобщенной силой, соответствующей искомому перемещению, то есть:
-
если мы хотим определить вертикальное перемещение какой-то точки, то в этой точке следует приложить сосредоточенную силу, положить ее равной единице и найти изгибающий момент, вызванный действием только этой силы;
-
если требуется найти угол поворота какого-то сечения, то в этом сечении надо приложить сосредоточенную пару, равную единице, и найти изгибающий момент от этой пары;
-
подставить произведение изгибающих моментов от нагрузки и от единичной обобщенной силы в интеграл (4.21) и проинтегрировать по всей длине конструкции.
Очень распространенным
способом интегрирования формулы
Максвелла – Мора является способ
графического интегрирования, называемый
правилом Верещагина.
Для того, чтобы воспользоваться правилом
Верещагина, надо построить графики
функций М
и
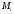 ,
входящих в подынтегральное выражение
формулы Максвелла – Мора. Такими
графиками являются эпюры М
и
,
входящих в подынтегральное выражение
формулы Максвелла – Мора. Такими
графиками являются эпюры М
и
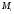 .
Операция интегрирования формулы
Максвелла – Мора с помощью правила
Верещагина носит название "перемножение
эпюр". Правило Верещагина состоит в
следующем:
.
Операция интегрирования формулы
Максвелла – Мора с помощью правила
Верещагина носит название "перемножение
эпюр". Правило Верещагина состоит в
следующем:
-
Разбиваем эпюру М на простые фигуры, для которых известно положение центра тяжести (прямоугольники, треугольники и т. п.)
-
Находим площади этих фигур
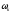 .
При определении площадей учитываем
знаки ординат.
.
При определении площадей учитываем
знаки ординат.
-
Под центрами тяжести этих фигур находим ординаты
 на эпюре
на эпюре
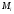 (с учетом знаков).
(с учетом знаков).
-
Искомый интеграл будет равен (при постоянной жесткости балки
 )
сумме произведений площадей
)
сумме произведений площадей
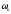 на соответствующие им ординаты под
центрами тяжести
на соответствующие им ординаты под
центрами тяжести
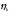 ,
то есть
,
то есть
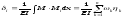 ,
(4.22) где n
– количество фигур, на которые разбита
эпюра М.
,
(4.22) где n
– количество фигур, на которые разбита
эпюра М.
Вторым способом графического интегрирования формулы Максвелла – Мора является способ, использующий формулу Симпсона. Эта формула получена из известной в математике формулы Симпсона приближенного интегрирования путем деления участка интегрирования на два отрезка. Если подынтегральные функции М и Мi – линейные или квадратные параболы, то формула Симпсона дает точное значение интеграла. Приведем эту формулу, применяемую для перемножения эпюр,
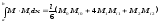 .
(4.25) В написанной формуле
.
(4.25) В написанной формуле
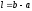 – длина участка интегрирования;
– длина участка интегрирования;
 и
и
 – значения крайних ординат на эпюрах
М
и Мi;
– значения крайних ординат на эпюрах
М
и Мi;
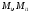 –
ординаты на эпюрах М
и Мi,
вычисленные в середине участка
перемножения
–
ординаты на эпюрах М
и Мi,
вычисленные в середине участка
перемножения
Статически неопределимые балки и рамы – конструкции, в которых уравнений статики недостаточно для определения опорных реакций и внутренних усилий. Число связей, наложенных на статически неопределимую систему, больше того количества связей, которые обеспечивают геометрическую неизменяемость конструкции.
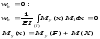
Метод
начальных параметров.
Если балка имеет
 участков, то функция изгибающего момента
участков, то функция изгибающего момента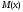 на каждом участке своя. Если использовать
специальные правила записи и интегрирования
дифференциального уравнения, которые
называются правилами
Клебша, то
число произвольных постоянных можно
свести к двум, независимо от количества
участков в балке. Перечислим эти правила:
на каждом участке своя. Если использовать
специальные правила записи и интегрирования
дифференциального уравнения, которые
называются правилами
Клебша, то
число произвольных постоянных можно
свести к двум, независимо от количества
участков в балке. Перечислим эти правила:
-
Начало координат для всех участков должно быть единым и находиться на конце балки (левом или правом) (рис. 4.16).
-
При составлении выражения для изгибающего момента на каждом участке рассматриваем всегда все силы с той стороны от сечения, где находится начало координат.
-
Если на балку действует распределенная нагрузка, которая обрывается в каком-то сечении балки, то ее следует продолжить до конца балки и приложить на участке, где добавлена нагрузка, распределенную нагрузку той же интенсивности, но противоположного знака (Конец балки всегда противоположен выбранному началу координат.)
-
Если к балке приложена сосредоточенная пара сил
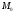 ,
то в выражение для изгибающего момента
она входит с множителем
,
то в выражение для изгибающего момента
она входит с множителем
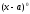 ,
где а
– расстояние от начала координат до
места приложения пары сил.
,
где а
– расстояние от начала координат до
места приложения пары сил. -
Интегрирование ведется без раскрытия скобок, то есть
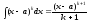 .
Можно показать, что для балки с произвольным
числом участков при использовании
правил Клебша произвольные постоянные
.
Можно показать, что для балки с произвольным
числом участков при использовании
правил Клебша произвольные постоянные
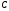 и
и
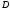 имеют следующий геометрический смысл:
имеют следующий геометрический смысл:
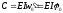
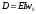 Например, при выборе начала отсчета
координаты х
следует помещать начало координат в
тот конец балки, где есть какое-нибудь
закрепление.
Например, при выборе начала отсчета
координаты х
следует помещать начало координат в
тот конец балки, где есть какое-нибудь
закрепление.
Универсальные уравнения для определения углов и прогибов балки при изгибе:
Если
после снятия возмущения
стержень возвращается в исходное
прямолинейное состояние, то это состояние
называется устойчивым.
Если же после удаления возмущающей
нагрузки стержень остается в изогнутом
состоянии, то первоначальная прямолинейная
форма равновесия является неустойчивой.
Нагрузка, при которой первоначальная
форма равновесия становится неустойчивой,
называется критической.
Определение
критической нагрузки.
Перед отысканием критической силы надо
найти величину гибкости стержня
 ,
которая ищется по формуле
,
которая ищется по формуле
 где l
– длина стержня;
где l
– длина стержня;
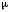 –
коэффициент, зависящий от условий
закрепления стержня;
–
коэффициент, зависящий от условий
закрепления стержня;
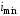 – минимальный радиус инерции поперечного
сечения стержня.
– минимальный радиус инерции поперечного
сечения стержня.
В
зависимости от величины
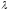 определение критической силы для
стержней из пластичного материала нужно
производить по трем формулам:
определение критической силы для
стержней из пластичного материала нужно
производить по трем формулам:
-
если
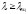 (стержень
большой гибкости), то критическая сила
определяется по формуле Эйлера
(стержень
большой гибкости), то критическая сила
определяется по формуле Эйлера
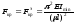
-
если
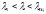 (стержень
средней гибкости), то для нахождения
критической силы используется формула
Ясинского
(стержень
средней гибкости), то для нахождения
критической силы используется формула
Ясинского

;
если
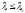 (стержень
малой гибкости), то
(стержень
малой гибкости), то
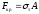
Величины
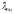 ,
,
 ,
коэффициенты a
и b
в формуле Ясинского зависят от материала.
Значение
,
коэффициенты a
и b
в формуле Ясинского зависят от материала.
Значение
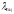 находится из условия, что критическое
напряжение, найденное по формуле Эйлера,
не должно превышать
находится из условия, что критическое
напряжение, найденное по формуле Эйлера,
не должно превышать
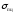 (материал
должен подчиняться закону Гука). Из
этого условия можно найти
(материал
должен подчиняться закону Гука). Из
этого условия можно найти

.
Условия
устойчивости и прочности.
Условием устойчивости центрально-сжатого
стержня является условие
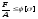
где
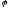 – коэффициент понижения допускаемых
напряжений (или коэффициент продольного
изгиба), зависящий от гибкости и материала
стержня
– коэффициент понижения допускаемых
напряжений (или коэффициент продольного
изгиба), зависящий от гибкости и материала
стержня
Из
условия устойчивости (6.6), если известны
размеры сечения, можно найти значение
допускаемой нагрузки
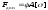
Для
центрально-сжатых стержней малой и
средней гибкости более опасным, чем
условие устойчивости, может оказаться
условие прочности, которое записывается
в таком виде:
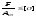 Здесь
Здесь
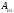 – так называемая площадь нетто, т. е.
площадь сечения, равная полной площади
– так называемая площадь нетто, т. е.
площадь сечения, равная полной площади
 ,
уменьшенной на площадь
,
уменьшенной на площадь
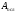 ,
занятую ослаблениями (отверстиями,
выточками):
,
занятую ослаблениями (отверстиями,
выточками):
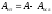 .
.
Определение
коэффициента запаса устойчивости.
Нормируемый коэффициент запаса
устойчивости определяется по формуле
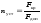 где
допускаемая нагрузка находится из
условия устойчивости (6.7). Обычно
нормируемый коэффициент запаса
устойчивости больше, чем нормируемый
коэффициент запаса прочности, и для
пластичных материалов находится в
пределах
где
допускаемая нагрузка находится из
условия устойчивости (6.7). Обычно
нормируемый коэффициент запаса
устойчивости больше, чем нормируемый
коэффициент запаса прочности, и для
пластичных материалов находится в
пределах
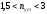 .
.
Действительный
коэффициент запаса устойчивости
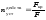 Поскольку
размеры сечения могут быть любыми,
используем метод
последовательных приближений.
Примем
Поскольку
размеры сечения могут быть любыми,
используем метод
последовательных приближений.
Примем
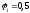 .
Из условия устойчивости найдем площадь
сечения.
.
Из условия устойчивости найдем площадь
сечения.
Динамическая нагрузка — нагрузка, характеризующаяся быстрым изменением во времени её значения, направления или точки приложения и вызывающая в элементах конструкции значительные силы инерции.
Наиболее часто встречающимися динамическими нагрузками являются:
-
силы инерции, возникающие при движении тела с ускорением, в том числе в процессе колебаний элементов конструкций;
-
ударные нагрузки, т. е. нагрузки, прикладываемые за очень короткий промежуток времени;
-
циклические нагрузки, меняющиеся во времени по определенному циклу.
Динамический
коэффициент –
есть величина, сопоставляющее динамическое
значение некоторого фактора (усилия,
напряжения, перемещения) с соответствующим
статическим
значением
этого фактора, в виде отношения: 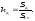
Влияние
ударной нагрузки на напряжения и
деформации конструкции оценивается с
помощью динамического
коэффициента
 ,
который можно определить по следующей
формуле:
,
который можно определить по следующей
формуле:
 где h
– высота падения груза;
где h
– высота падения груза;
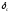 – вертикальное перемещение точки
приложения груза при статическом его
приложении.
– вертикальное перемещение точки
приложения груза при статическом его
приложении.
Формула
(7.4) является достаточно грубой оценкой
влияния ударной нагрузки, так как она
получена с использованием ряда упрощающих
задачу допущений. Одним из этих допущений
является предположение о том, что
материал конструкции в момент удара
работает в упругой стадии (подчиняется
закону Гука). Зная динамический
коэффициент, можно найти динамические
(возникающие под действием ударной
нагрузки) напряжения
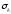 в конструкции по формуле
в конструкции по формуле
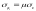 ,где
,где
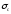 – напряжения от статического (медленного)
приложения нагрузки. В
– напряжения от статического (медленного)
приложения нагрузки. В
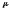 раз (справедлив закон Гука) увеличиваются
и деформации конструкции от ударной
нагрузки по сравнению со статическими
деформациями.
раз (справедлив закон Гука) увеличиваются
и деформации конструкции от ударной
нагрузки по сравнению со статическими
деформациями.
К динамическим нагрузкам, несмотря на отсутствие значительных инерционных сил, можно отнести периодические многократно повторяющиеся (циклические) нагрузки, действующие на элементы конструкции.
Как показывает практика, нагрузки, циклически изме-няющиеся во времени по величине или по величине и по знаку, могут привести к разрушению конструкции при напряжениях, существенно мень-ших, чем предел текучести (или предел прочности). Такое разрушение принято называть «усталостным». Материал как бы «устает» под действием многократных перио-дических нагрузок.
