
- •1.Понятие статистики. Структура современной статистической науки
- •2.Теоритические основы статистики как науки.
- •3. Особенности предмета статистики.
- •4. Статистическая методология.
- •5. Основные задачи и принципы организации государственной статистики в рф
- •6. Понятие статистического наблюдения, этапы его проведения
- •7. Статистическое наблюдение: понятие , формы статистического наблюдения.
- •8. Виды статистического наблюдения.
- •9. Способы статистического наблюдения.
- •10.Программно-методологические вопросы статистического наблюдения
- •11. Организационные вопросы статистического наблюдения
- •12. Ошибки статистического наблюдения
- •14. Метод группировки и его место в экономическом анализе
- •15. Виды статистической группировки
- •16. Статистическая группировка: Принципы выбора группировочного признака. Образование групп и интервалов группировки
- •17. Статистические ряды распределения
- •Вопрос 22.Средние величины
- •Вопрос 23.Средняя арифметическая и ее свойства
- •Вопрос 24.Другие виды средних: средняя гармоническая и средняя геометрическая
- •Вопрос 25.Структурные средние величины (мода и медиана)
- •Вопрос 26 Мода и медиана в интервальном ряду распределения.
- •Вопрос 27. Показатели вариации и ее значение.
- •Вопрос 28. Показатели вариации и их значение в статистике.
- •Вопрос 29.Дисперсия:свойства и методы расчета.
- •Вопрос 30 Виды дисперсий и закон сложения дисперсий
- •Вопрос 31. Статистические ряды динамики:определение структура.
- •Вопрос 32. Статистические ряды динамики:понятие,виды,правила построения.
- •33. Абсолютные и относительные показатели анализа рядов динамики.
- •34. Система средних показателей рядов динамики.
- •35. Основные приемы обработки и анализа рядов динамики.
- •36. Экономические индексы: понятие, классификация.
- •37.Индивидуальные индексы: понятие, основные виды.
- •38. Сводные (общие) индексы: понятие, основные виды, их взаимосвязи.
- •39. Сводные индексы в средней арифметической и средней гармонической формах.
- •42. Индексы пространственно – территориального сопоставления.
- •43. Важнейшие экономические индексы и их взаимосвязи.
Вопрос 22.Средние величины
Наиболее распространенной формой статистических показателей, используемой в социально-экономических исследованиях, является средняя величина.
Средняя величина представляет собой обобщенную количественную характеристику статистической совокупности в конкретных условиях места и времени. Сущность средней состоит в том, что она отражает типичный уровень признака и абстрагируется от индивидуальных особенностей, присущих отдельным единицам. Средняя величина только тогда будет отражать типичный уровень признака, когда она рассчитана по качественно однородной совокупности.
Определить среднюю во многих случаях можно через исходное соотношение средней (ИСС) или ее логическую формулу:
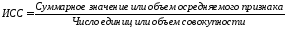 .
(4.9)
.
(4.9)
В
каждом конкретном случае для реализации
исходного соотношения требуется одна
из форм средней величины. Все виды
средних объединяются в общей формуле
средней
степенной
(при различной величине
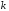 ):
):
1) простая:
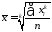 ,
(4.10)
,
(4.10)
2) взвешенная:
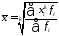 ,
(4.11)
,
(4.11)
где
 - показатель степени, определяющий вид
средней величины;
- показатель степени, определяющий вид
средней величины;
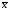 -
средняя величина исследуемого явления;
-
средняя величина исследуемого явления;
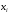 –
–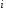 -ый
вариант осредняемого признака
-ый
вариант осредняемого признака
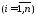 ;
;
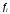 –вес
–вес
 -го
варианта.
-го
варианта.
В
зависимости от
 различают следующие виды средних
величин:
различают следующие виды средних
величин:
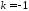 –средняя
гармоническая;
–средняя
гармоническая;
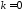 –средняя
геометрическая;
–средняя
геометрическая;
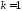 -
средняя арифметическая;
-
средняя арифметическая;
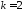 –средняя
квадратическая.
–средняя
квадратическая.
Вопрос 23.Средняя арифметическая и ее свойства
Наиболее распространенным видом средних величин является средняя арифметическая, которая в зависимости от характера имеющихся данных может быть простой или взвешенной.
Средняя арифметическая простая применяется, когда значение вариантов встречается по одному числу раз.
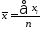 .
(4.12)
.
(4.12)
Средняя арифметическая взвешенная применяется, когда отдельное значение признака повторяется неодинаковое количество раз, т.е. она используется в расчетах средней по сгруппированным данным или вариационным рядам, которые могут быть дискретными и интервальными.
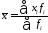 .
(4.13)
.
(4.13)
При расчете средней по интервальному вариационному ряду для выполнения необходимых вычислений переходят от интервалов к их серединам.
Например, по данным таблицы 4.2 определим величину среднедушевого дохода по городу.
Таблица 4.2 - Распределение населения города в 1-м квартале 2010г. по уровню среднедушевых денежных доходов
|
Среднедушевой денежный доход в среднем за месяц, тыс. руб. |
Численность населения, % к итогу |
|
До 5000 |
10,5 |
|
5000-10000 |
30,2 |
|
10000 – 15000 |
24,3 |
|
15000 – 20000 |
16,7 |
|
20000 – 25000 |
13,2 |
|
Свыше 25000 |
5,1 |
|
Итого |
100 |
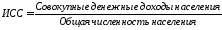 .
(4.14)
.
(4.14)
Так как мы имеем интервальный ряд, то определяем середины интервалов. При этом величину первого интервала условно приравниваем к величине второго, а величину последнего интервала приравниваем к величине предпоследнего. В результате получаем следующие середины интервалов:

Роль численности населения выполняет его доля в общем итоге, выраженная в процентах. Для расчета воспользуемся формулой средней арифметической взвешенной:
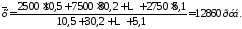
Средняя арифметическая обладает следующими свойствами:
1. Произведение средней на сумму частот равно сумме произведений отдельных вариантов на соответствующие им частоты:
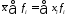 .
(4.15)
.
(4.15)
2. Свойство для отклонений: сумма отклонений вариант от средней арифметической равно нулю:
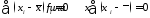 .
(4.16)
.
(4.16)
3. Свойство для
вариант: если все осредняемые уменьшить
или увеличить на постоянное число
 ,
то средняя арифметическая соответственно
уменьшится или увеличится на ту же
величину:
,
то средняя арифметическая соответственно
уменьшится или увеличится на ту же
величину:
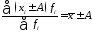 .
(4.17)
.
(4.17)
4. Если варианту увеличить или уменьшить в какое-то число раз, то в то же число раз увеличится или уменьшится среднее арифметическое:
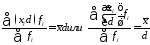 .
(4.18)
.
(4.18)
5. Свойство для частот: если частоты (веса) ряда увеличить или уменьшить на произвольное число, то средняя арифметическая от этого не изменится:
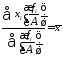 .
(4.19)
.
(4.19)
6. Если веса или частоты всех вариант равны между собой, то средняя арифметическая взвешенная будет равна средней арифметической простой:
 ,
если
,
если
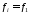 .
(4.20)
.
(4.20)
Знание основных свойств средней арифметической позволяет упростить ее вычисление, особенно для вариационного ряда с равными интервалами, т.е. способом моментов:
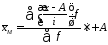 ,
(4.21)
,
(4.21)
где
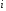 – интервал;
– интервал;
 –серединное
значение интервала;
–серединное
значение интервала;
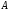 –условная величина;
–условная величина;
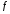 -
частота признака.
-
частота признака.
За условную
величину (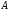 )
принимают варианту, занимающую серединное
положение в данном ряду и имеющую
наибольшую частоту.
)
принимают варианту, занимающую серединное
положение в данном ряду и имеющую
наибольшую частоту.
Доминирующее серединное положение в ряду:
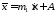 ,
(4.22)
,
(4.22)
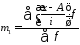 .
.
Серединное
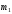 из значений
из значений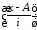 называетсямоментом
первого порядка.
называетсямоментом
первого порядка.
