
№1 Интерполяция функций. ИП Лагранжа
В вычислительной математике существенную роль играет интерполяция функций, т.е. построение по заданной функции другой (как правило, более простой), значения которой совпадают со значениями заданной функции в некотором числе точек. Причем интерполяция имеет как практическое, так и теоретическое значение. На практике часто возникает задача о восстановлении непрерывной функции по ее табличным значениям, например полученным в ходе некоторого эксперимента. Для вычисления многих функций оказывается эффективно приблизить их полиномами или дробно-рациональными функциями. Теория интерполирования используется при построении и исследовании квадратурных формул для численного интегрирования, для получения методов решения дифференциальных и интегральных уравнений.
Пусть на отрезке [a,b] задана функция ƒ(x). Задача интерполяции (или интерполирования) состоит в построении функции g(x), совпадающей с заданной ƒ(x) в некотором наборе точек {x1,x2,...,xn+1} из отрезка [a,b] (эти точки называются узлами интерполяции), т.е. должны выполняться условия:
g(xk)=yk, k=1,2,...,n+1,
где yk - известные значения функции ƒ(x) в точках xk. Функция g(x) называется интерполянтом функции ƒ(x).
Пример интерполяции с четырьмя узлами приведен на следующем рисунке
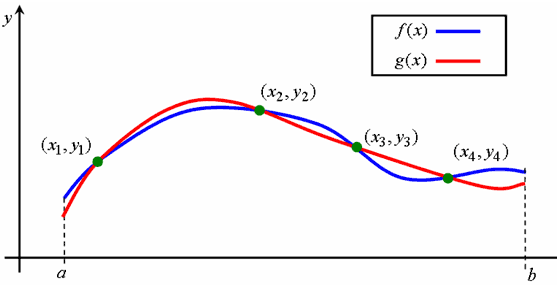
из которого видно, что узлы интерполяции не обязательно должны располагаться равномерно на отрезке [a,b].
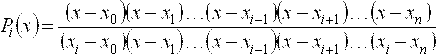 .
(6)
.
(6)
Степень полинома равна п. Нумерация точек начинается с 0 и заканчивается п, при этом i-я точка выпадает. Полученный полином представляет исходную функцию у = F(x) только в одной точке. Для представления всей таблично заданной функции таких полиномов потребуется п.
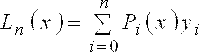 .
(7)
.
(7)
Рассмотрим частные случаи полинома Лагранжа при п=1; п=2; п=3.
Для п=1 исходная таблица функции будет выглядеть следующим образом:
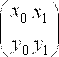 ,
,
Тогда по формуле (7) имеем
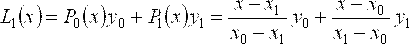 .
.
Для случая п = 2:
 .
.
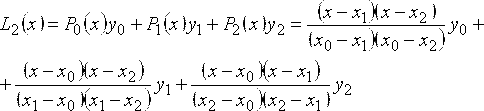
Для случая п=3:
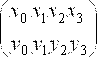 .
.
![]()
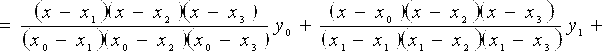
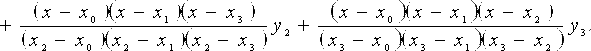
|
№2 Конечные разности и их свойства |
|
|
|
|
Величина
Называется Конечной разностью первого порядка (или разностью «на шаг вперед»).
Свойства конечных разностей.
1.
Операторы
.
2.
3.
Операторы
5.
Таким
образом для полинома
|
№3-4 ИПН Ньютона
Пусть
![]() -
сетка равноотстоящих узлов
-
сетка равноотстоящих узлов
Введем безразмерную переменную
![]() ,
а выражения вида
,
а выражения вида
![]() —
конечные
разности.
—
конечные
разности.

|
|
(18) |
Формула (18) называется Первой интерполяционной формулой Ньютона или Формулой «интерполирования вперед»
Приведем простейшие частые случаи интерполяции по Ньютону:
1)
Линейная интерполяция,
![]() :
:
![]() .
.
2)
Квадратичная интерполяция,
![]() :
:
![]() .
.
вторая
интерполяционная формула Ньютона,
применяется для интерполирования
назад:
![]() где
где
![]()
№9 Аппроксимация по МНК каноническим полиномом.
Выберем базисные функции в виде последовательности степеней аргумента x:
φ0(x) = x0 = 1; φ1(x) = x1 = x; φm(x) = xm, m < n.
Расширенная матрица Грама для степенного базиса будет выглядеть следующим образом:
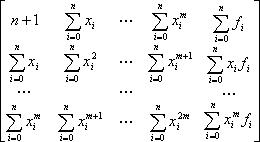
Особенность вычислений такой матрицы (для уменьшения количества выполняемых действий) состоит в том, что необходимо сосчитать только элементы первой строки и двух последних столбцов: остальные элементы заполняются сдвигом предшествующей строки (за исключением двух последних столбцов) на одну позицию влево. В некоторых языках программирования, где отсутствует быстрая процедура возведения в степень, пригодится алгоритм расчета матрицы Грама, представленный далее.
Выбор базисных функций в виде степеней x не является оптимальным с точки зрения достижения наименьшей погрешности. Это является следствием неортогональности выбранных базисных функций. Свойство ортогональности заключается в том, что для каждого типа полинома существует отрезок [x0, xn], на котором обращаются в нуль скалярные произведения полиномов разного порядка:
![]() ,
j ≠ k, ρ – некоторая весовая
функция.
,
j ≠ k, ρ – некоторая весовая
функция.
Если
бы базисные функции были ортогональны,
то все недиагональные элементы матрицы
Грама были бы близки к нулю, что увеличило
бы точность вычислений, в противном
случае при
![]() определитель
матрицы Грама очень быстро стремится
к нулю, т.е. система становится плохо
обусловленной.
определитель
матрицы Грама очень быстро стремится
к нулю, т.е. система становится плохо
обусловленной.
№10 Численное дифференцирование на основе интерполяции Ньютона
Если
функция
![]() задана
таблично, то аналитическое дифференцирование
невозможно. Строится интерполяционный
полином и его производную принимают
приближенно за
задана
таблично, то аналитическое дифференцирование
невозможно. Строится интерполяционный
полином и его производную принимают
приближенно за
![]() .
.
Запишем 1-ую форму интерполяционного полинома Ньютона на равномерной сетке:
|
|
(1) |
Где
![]()
![]() .
.
![]() -
погрешность интерполяции.
-
погрешность интерполяции.
Дифференцируя (1), получим:
![]() ,
,
Где
![]() -
-
- теоретическая погрешность производной.
№11
В основе численного дифференцирования лежит аппроксимация функции, от которой берется производная, интерполяционным многочленом
Вычисление производных на основе интерполяционных многочленов Лагранжа
Предположим,
что некоторая функция задана таблицей
значений yi
= f(xi),
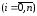 с постоянным шагом аргумента h
= xi
– xi-1
с постоянным шагом аргумента h
= xi
– xi-1
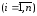 .
Для того, чтобы выразить значение
производной через значения функции в
узлах интерполяции, запишем интерполяционный
многочлен Лагранжа степени m,
удовлетворяющий условиям Lm(xk)
= yk
= f(xk),
.
Для того, чтобы выразить значение
производной через значения функции в
узлах интерполяции, запишем интерполяционный
многочлен Лагранжа степени m,
удовлетворяющий условиям Lm(xk)
= yk
= f(xk),
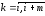 :
:
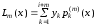 ,
,
где лагранжевы коэффициенты вычисляются как
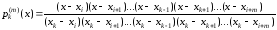 .
.
Дифференцируя
этот многочлен, можно получить приближенные
значения производных в узлах
интерполирования xk
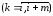 .
.
В частности, для m = 1 получим:
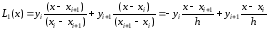 ;
;
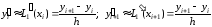 .
.
численный дифференцирование производная интерполяционный
Пусть m = 2. Тогда
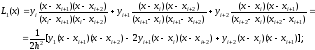
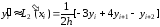 ,
(5)
,
(5)
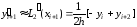 ,
(6)
,
(6)
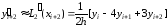 .
(7)
.
(7)
В целом для отрезка [x0, xn] рекомендуется вычислять производные следующим образом:
а) значение y(x0) - по формуле (5), где xi = x0;
б)
значения
y(xi)
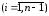 -
по формуле (6), где xi+1
-
по формуле (6), где xi+1
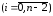 ;
;
в) значение y(xn) - по формуле (7), где xi+2 = xn.
№12 ЧисленДиффМетод неопределенных коэффициентов
Аналогичные формулы можно получить и для случая произвольного расположения узлов. Использование многочлена Лагранжа в этом случае приводит к вычислению громоздких выражений, поэтому удобнее применять метод неопределенных коэффициентов. Он заключается в следующем. Искомое выражение для производной k-гo порядка в некоторой точке х = xiпредставляется в виде линейной комбинации заданных значений функции в узлах x0 , x1,... ,xn:
![]() (3.10)
(3.10)
Предполагается, что это соотношение выполняется точно, если функция у является многочленом степени не выше n, т.е. может быть представлена в виде
![]()
Отсюда
следует, что соотношение (3.10), в частности,
должно выполняться точно для многочленов
у — 1, у = х - х0,... ,![]() .
Подставляя последовательно эти
выражения в (3.10) и требуя выполнения
точного равенства, получаем систему п
+ 1 линейных алгебраических уравнений
для определения неизвестных коэффициентов
с0, с1,..., сn.
.
Подставляя последовательно эти
выражения в (3.10) и требуя выполнения
точного равенства, получаем систему п
+ 1 линейных алгебраических уравнений
для определения неизвестных коэффициентов
с0, с1,..., сn.
Пример.
Найти выражение для производной
![]() в
случае четырех равноотстоящих узлов
(n=3).
в
случае четырех равноотстоящих узлов
(n=3).
Приближение (3.10) запишется в виде
![]() (3.11)
(3.11)
Используем следующие многочлены:
![]() (3.12)
(3.12)
Вычислим их производные:
![]() (3.13)
(3.13)
Подставим последовательно соотношения (3.12) и (3.13), соответственно в правую и левую части (3.11) при х = х1, требуя выполнения точного равенства:
![]()
![]()
Получим окончательно систему уравнений в виде
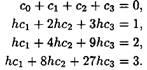
Решив эту систему, получим
![]()
Подставив эти значения в (3.11), найдем выражение для производной:
![]()
№13
|
Формула прямоугольников |
|
|
|
|
На частичном отрезке [Xi-1, Xi] заменим подынтегральную функцию полиномом Лагранжа нулевого порядка, построенным в одной точке. Естественно в качестве этой точки выбрать среднюю: Xi-0.5 = Xi - 0.5H. Тогда получим формулу
Подставив (2.6) в (2.5), получим составную формулу средних прямоугольников:
Графическая иллюстрация метода средних прямоугольников представлена на рис. 2.1.
Рис. 2.1. Интегрирование методом средних прямоугольников Погрешность формулы (2.7) определяется выражением
Здесь
Замечание. Формулу (2.7) можно представить в ином виде:
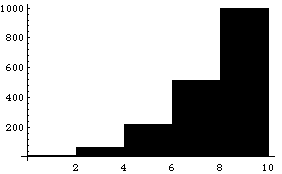
Эти формулы в выражении (2.9) называются формулой левых и правых прямоугольников соответственно. Графически метод левых и правых прямоугольников представлен на рис. 2.2.
А) б) Рис. 2.2. Метод левых (а) и правых (б) прямоугольников Однако из-за нарушения симметрии в формулах (2.9) их погрешность значительно больше, чем в методе средних прямоугольников и ~O(H). |
№14
|
Формула трапеций |
|
|
|
|
Если на частичном отрезке подынтегральную функцию заменить полиномом Лагранжа первой степени, то есть
Тогда искомый интеграл запишется следующим образом:
После подстановки выражения (2.11) в (2.5) составная формула трапеций примет вид
Графически метод трапеций представлен на рис. 2.3.
Рис. 2.3. Метод трапеций Погрешность формулы (2.12) определяется выражением:
Таким образом, погрешность метода трапеций Ψ ~ O(H²), но она в два раза больше, чем для формулы средних прямоугольников. |
№ 15 Метод Парабол он же Симпсона
В этом методе предлагается подынтегральную функцию на частичном отрезке аппроксимировать параболой, проходящей через точки (Xj, F(Xj)), где J = I-1; I-0.5; I, то есть подынтегральную функцию аппроксимируем интерполяционным многочленом Лагранжа второй степени:
![]()
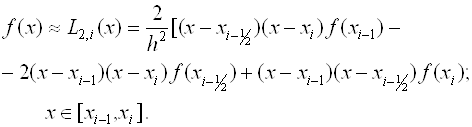 (2.14)
(2.14)
Проведя интегрирование, получим:
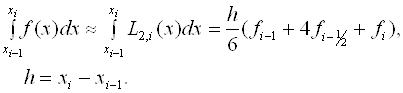
![]() (2.15)
(2.15)
Это и есть Формула Симпсона или формула парабол. На отрезке [A, B] формула Симпсона примет вид
![]()
 (2.16)
(2.16)
Графическое представление метода Симпсона показано на рис. 2.4.
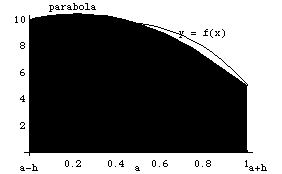
Рис. 2.4. Метод Симпсона
Избавимся в выражении (2.16) от дробных индексов, переобозначив переменные:
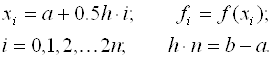 (2.17)
(2.17)
Тогда формула Симпсона примет вид
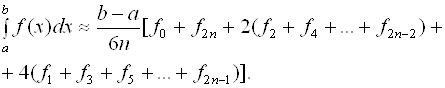 (2.18)
(2.18)
Погрешность формулы (2.18) оценивается следующим выражением:
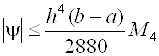 ,
(2.19)
,
(2.19)
Где
H·N = B - A,
![]() .
Таким образом, погрешность формулы
Симпсона пропорциональна O(H4).
.
Таким образом, погрешность формулы
Симпсона пропорциональна O(H4).
Замечание. Следует отметить, что в формуле Симпсона отрезок интегрирования обязательно разбивается на Четное число интервалов.
№ 16 Задача Коши методом Эйлера
Пусть дана задача Коши для уравнения первого порядка
![]()
![]()
где
функция
![]() определена
на некоторой области
определена
на некоторой области
![]() .
Решение ищется на интервале
.
Решение ищется на интервале
![]() .
На этом интервале введем узлы
.
На этом интервале введем узлы
![]()
Приближенное
решение в узлах
![]() ,
которое обозначим через
,
которое обозначим через
![]() определяется
по формуле
определяется
по формуле
![]()
Эти формулы обобщаются на случай систем обыкновенных дифференциальных уравнений.

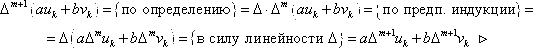

 .
(2.6)
.
(2.6) .
(2.7)
.
(2.7)
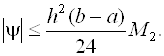 (2.8)
(2.8)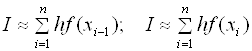 .
(2.9)
.
(2.9)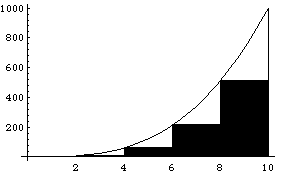
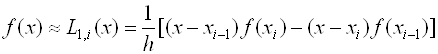 ,
(2.10)
,
(2.10)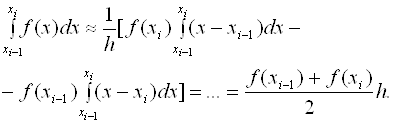 (2.11)
(2.11)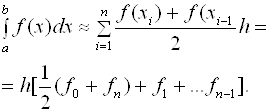 (2.12)
(2.12)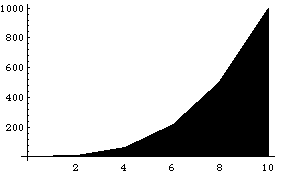
 (2.13)
(2.13)