Лабораторная работа №3

Лабораторная работа №3

Исследование математических моделей на основе уравнений и систем

1.Цель работы.

Получение студентами практических навыков решения математических моделей на основе нелинейных алгебраических и трансцендентных уравнений, а также систем линейных уравнений в среде пакета MathCAD и в ручном режиме.

2. Краткие сведения из теории

С практической точки зрения построение математической модели объекта теоретическим, формально-статистическим или комбинированным методом – лишь один из этапов в решении инженерной или научно-исследовательской задачи, касающейся этого объекта. В дальнейшем модель исследуется на предмет адективности оригиналу (экспериментальными и статистическими методами) и возможности ее использования для решения на ее основе различных прикладных задач. В том случае, когда построенная модель изначально была ориентирована на конкретную задачу или задачи одного типа, объединенные общностью их математической поставки, говорят о «решении модели» с задаваемыми численными значениями ее параметров.

Существенное место среди функционерных математических моделей, полученных прежде всего теоретическим методом, занимают модели на основе уравнений и их систем. Решение таких моделей эквиватентно собственно решению соответствующих уравнений или систем, а трудоемкость этой процедуры определяется их особенностями.

Аналитическим решением обладает очень ограниченное число задач. Чтобы найти корни уравнения в виде выражения, требуется выразить одну переменную через все остальные (или коэффициенты). Сделать это обычно можно только в том случае, если уравнение включает переменные невысокой степени (до пятой) и не содержит разнообразных функций, делающих его транцендентными.

Численно можно решить практически любое уравнение. Однако получаемое при этом значение корня в виде числа менее информативно, чем выражение аналитического решения. Особенность численного решения – его приближенный характр, в то время как аналитическое является абсолютно точным и свободно от погрешностей.

Опыт показывает, что простые уравнения лучше решать аналитически, а сложные – численно.

Иногда встречаются такие уравнения, которые нельзя решать ни аналитически (так как они слишком сложны), ни численным (чаще всего потому, что соответствующая функция не является непрерывной). В таких случаях решение ищут графическим методом.

Аналитическое решение уравнений

Поиск аналитического решения (или решений) уравнения в ручном режиме проводится традиционным методом последовательных математических преобразований и выражения искомой величины через все остальные.

В MathCAD для этого существует несколько путей:

- непосредственное применение оператора solve в комбинации с оператором символьного вывода (при необходимости могут дополнительно или поэтапно использоваться операторы упрощения и преобразования expand, factor, collect, substitute, simplify, float и др.);

-применение вычислительного блока Giver/find без предварительного задания ожидаемого значения корня.

Лучше всего MathCAD справляется с поиском корней алгебраических полиномов (число корней таких полиномов равно степени полинома согласно теореме Гаусса).

Численное решение уравнений

Численные методы решения, как правило применяют в отношении нелинейных и трансцендентных уравнений. В основе этих методов лежит принцип подбора. В отличии от стихийного перебора всех возможных корней «вслепую», в численных методах процесс подбора является строго направленным на приближение некоторого промежуточного значения искомой переменной к кормю. Такое приближение основано на повторении одного и того же действия или последовательности действий – интеграции, поэтому численные методы решения уравнении называют итерационными. Колическтво необходимых итераций определяется скоростью сходимости алгоритма (эффективностью) в результате требуемой точности. Эффективность различных численных алгоритмов может различаться весьма значительно, но это не значит, что что всегда надо выбирать самый быстрый из них: чес выше скорость сходимости к решению. Как многочисленные экстремумы. Перегибы. Разрывы или недифференцируемост функции в некоторых точках.

Обычно процесс решения уравнения общего вида f(x)=0 осуществляется в два этапа. На первом этапе проводят локализацию (изоляцию или отделение) корней, т.е.е определение их существования в принципе, оценку их количества и примерного расположения. На втором этапе уточняют корни, т.е. находят их значения с предварительно заданной ε.(в практических задачах решениями уравнения f(x)=0 считают все такие значения переменной x, которые отличаются по модулю от соответствующих точных значений x, обращаются в нуль f(x), не более, чем на величину ε).

Идея методов первого этапа базируется на очевидном свойстве непрерывных функций: корни функции (точки пересечения f(x) с горизонтальной осью Ox) обязательно лежат между соседними экстремумами функции. Локализацию корней проводят:

-графически (построение графику y=f(x);

-сканированием (последовательным поиском корней, начиная от множества пробных значений x; например, вычислением таблицы значений функции f(x) при изменении величины x на заданном интервале с выбранным шагом h_x или сравнением невязок для каждой центральной точки элементарной области);

-аналитически (поиском критических точек функции f(x), в которых производная равна нулю или не существует, с последующим определением знака функции в этих точках, числа смен знака и интервала локализации).

Идея методов второго этапа можно сгруппировать по трем основным направлениям: 1) поиск корня с заданной погрешностью сводится к перебору всех возможных значений аргумента с проверкой наличия решения; 2) поиск корны нелинейной функции заменяется поиском корны той или иной более простой функции (линейной, параболической), близкой к исходной нелинейной, итерационными процедурами; 3) нелинейное (или трансцендентное) уравнение f(x)=0 сводят к одной из форм вида g(x)= φ(x) и стремятся обеспечить равенство левой и правой частей итерационными процедурами. Условием окончания процесса решения уравнения (т.е. получения корня) может быть одно из двух возможных:

f(x*)≤илиx*- x^k≤ ε,где  и ε – предварительно заданные малые величины; k-номер итерации (второе условие часто заменяют на x^k+1-x^k≤ε). Условие окончания поиска выражается исходя из постановки задачи. Этот факт надо учитывать, так как часто применением разных условий может привести к существенно разным результатам.

Метод сканирования предусматривает разделение заданного интервала изменения x, где отделен корень, на отрезки, равные заданной погрешности ε, с последующим вычислением значений функции f(x) на концах этих отрезков.

Метод половинного деления (метод Больцано) – развитие метода сканированмия. Сначала интервал изоляции (отделения0 корня делится поплам и путем сравнения знаков функции а концах каждой из двух половин (например, по знаку произведения значений функции на концах) определяют ту половину, в которой содержится решение (знаки функции на концах должны различаться). Затем найденную половину опять делят пополам, снова выбирают одну из двух половин содержащую корень, и т.д. Условием окончания процедуры служит заданная величина интервала изоляции корня.

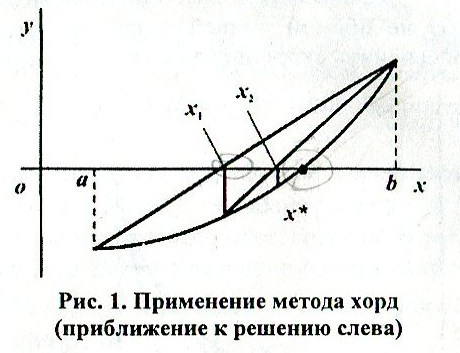
Метод хорд (секущих) предусматривает замену функции f(x) на интервале изоляции корня [a,b]линейной, в качестве которой берется хорда-прямая стягивающая концы нелинейной функции. Имея уравнение хорд, находят точку ее пересечения с осью Ox.Ее принимают за новую границу отрезка, где содержится корень. Через точку, соответствующую x₁ и границу предыдущего интервала опять проводят хорду, находят x₂ и т.д., получая последовательность x₃, x₄, x₅,…, сходящуюся к корню. Метод применим только для монотонных функций, а его алгоритм зависит от свойств функции f(x); при f(b)*f’’(b)0 хорда зафиксирована справа и

x_i+1=x_i-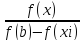*(b-x_i) (x₀=a); при f(b)*f’’(b)0 хорда зафиксирована слева и x_i+1=a+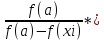(x_i-a) (x₀=b)

Метод касательных или линеаризации (метод Ньютона) похож на метод хорд, но в качестве прямой берется касательная, проводимая в текущей точке последовательности. Уравнение касательной находится по координате обратной точки и углу наклона (значение производной). В качестве начальной точки в зависимости от свойств функции берется или левая точка интервала изоляции x0=a (если f(b)*f’’(b)0), или правая точка x₀=b (если f(b)*f’’(b)0). При этом инерационная формула xi+1=xi-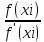

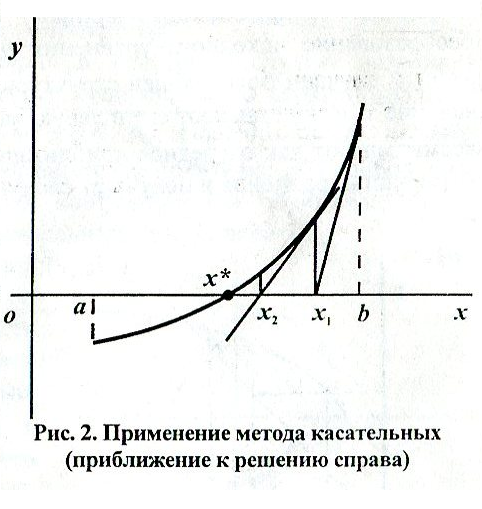
Метод работоспособен для выпуклых и монотонных функций. Главное достоинство метода – квадратичная скорость сходимости (у метода хорд – линейная), что может сократить количество итераций.

Комбинированный метод также базируется на замене нелинейной функции f(x) линейной, но с учетом стремления к корню методом хорд и методом Нютона с разных сторон: для повышения эффективности он использует оба алгоритма. Один шаг делается методом хорд, а следующий с другой стороны методом Ньютона. При этом интервал изоляции корня сокращается с обеих сторон. Поиск прекращается, когда разница между правым и левым концами интервала станет меньше предварительно заданной погрешности ε.

Метод параболической аппроксимации ориентирован на замену функции f(x) не прямой линией, а квадратичной параболой, и в связи с этим может обеспечить скорейшую сходимость к решению. На первом этапе параболу строят по трем точкам: x=a; x=b и x=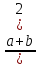. Коэффициенты в уравнении параболы y=c₂x²+c₁x+c₀ находят из системы уравнений – условий прохождений параболы через точки. Решая уравнение c₂x²+c₁x+c₀=0, находят приближенный корень. На втором этапе строят параболу по трем точкам: найденному приближенному корню и двум предыдущим точкам (слева и справа от этой точки), лежащим по разные стороны от оси Ox. Процедура повторяется, пока величина отрезка, внутри которого находится корень, не станет меньше предварительно заданной погрешности.

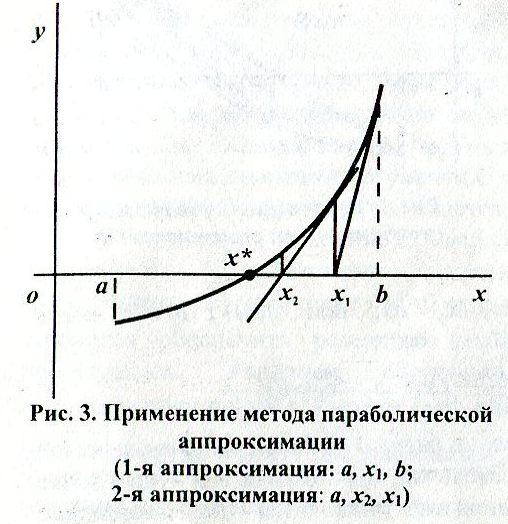
Метод простой итерации предусматривает предварительное преобразование исходного уравнения f(x)=0 к виду φ(x)=x, что является частным случаем более общей структуры g(x)=f(x). Затем выбирают начальное значение x₀ и подставляют его в левую часть уравнения. Полученное φ(x₀)=x₁ рассматривают как очередное приближение к корню. Его снова подставляют в левую часть уравнения и получают следующее значение φ(x₀)=x₂ и т.д.

Значения корня (его максимально возможное значение) и границы области их существованиянны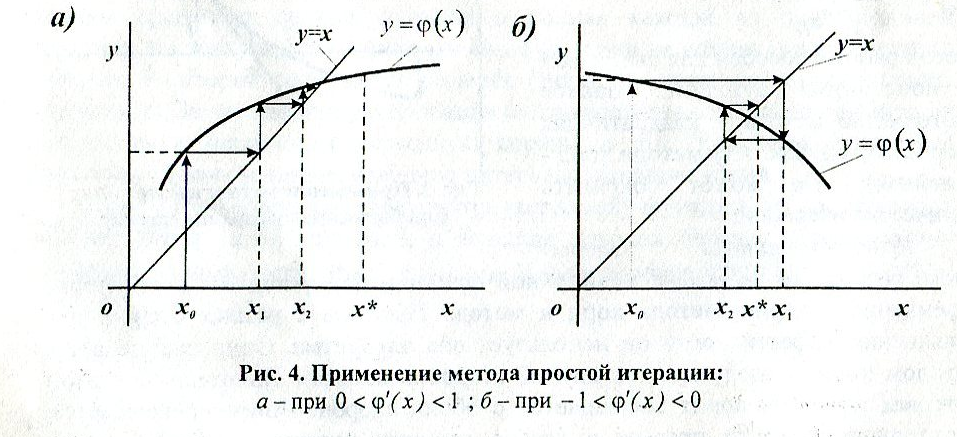

В общем виде итерационный процесс идет по схеме x_i+1=(x_i). Получающаяся таким образом последовательность x₀, x₁, x₂… при определенных условиях может сходиться к корню x*. Таким условием является (x)≤1 на [a,b], причем чем ближе модуль к нулю, тем выше скорость сходимости к решению.

Довольно часто при решении прикладных задач требуется определить число действительных корней, предельную оценку значение корня (его максимально возможное значение) и границы области их существования. В том случае, если в основе математической модели лежит уравнение со степенным полиномов P_n(x)=a₀x_n+a₁x_n-1+…a_n=0 (a₀0), проблему можно решить, не находя все корни, что особенно важно при ручном счете.

Для определения числа корней уравнения обычно используют теорему Гаусса и правило Декарта. В соответствии с теоремой Гаусса общее число действительных и комплексных корней полинома P_n(x) равно наивысшей степени полинома, т.е. n.

В соответствии с правилом Декарта количество действительных положительных корней либо равно числу перемен знака в последовательности коэффициентов уравнения P_n(-x)=0, либо на четное число меньше (равные нулю коэффициенты в обоих случаях не учитываются).

Предельную оценку значения корня в некоторых случаях позволяет проводить метод Лагранжа. Он сводится к определению верхней границы положительных корней по формуле R=1+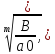a₀0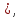 где m-номер первого по порядку отрицательного коэффициента полинома ; B – наибольшая из абсолютных величин отрицательных коэффициентов полинома. Метод применим к полиномам, имеющим отрицательные коэффициенты. 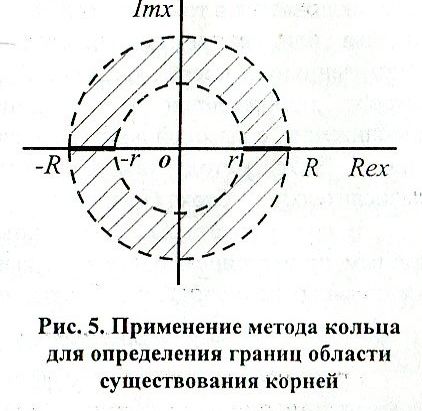Границы области существования корней устанавливаются с помощью метода кольца. Метод позволяет находить область существования всех корней уравнения P_n(x)=0, включая комплексные. Действительные корни находятся в интервале (-R;-r) и (r;R). 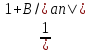Величины R и r вычисляются по формуле R=1+А/а₀; r= , где A= max {|a₁|, |a₂|…, |a_n|};

B=max{|a₁|, |a₂|…, |a_n-1|}. В случае нахождения области существования всех корней, в том числе комплексных, строится кольцо с радиусом r и R, внутри которого находятся все корни.Метод применим ко всем степенным полиномам P_n(x). Очевидно, что он позволяет и предельную оценку значения корня.

При проведении ручного счета значение хотя бы одного корня полинома P_n(x)

позволяет снизить трудоемкость решения задачи путем понижения порядка полинома. Так, если x₁- действительный корень полинома P_n(x), то новый полином

Pn-1(x)=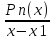

MathCAD позволяет численно решить уравнение с помощью встроенных функций root (реализует методы секущих и Больцано) для определения одного корня, polyroots (реализует специальные алгоритмы Легарра и парной матрицы) для поиска всех корней степенного полинома, оператора solvиe для поиска корней полинома любых порядков, вычислительные блоки Given/find (реализует метод Ньютона и другие градиетные алгоритмы) и Given/Minner (аналогичен предыдущему блоку и отличается от него только условием завершения работы – минимизация невязки вместо выполнения равенства) с предварительным заданием приближения корня.

Кроме того, MathCAD обеспечивают и прямую реализацию выше описанных методов в его среде. В большинстве случаев точность результатов зависит от величины заданных системных переменных TOL, определяющей точность сходимости, и CTOL, определяющей граничную точность при использовании блока Given/find.

Сравнивая эффективность методов Ньютона, Больцано и секущих, можно заключить, что алгоритм Ньютона сходится более быстро. Однако для метода Ньютона и секущих характерны трудности в поиске решений при наличии экстремумов, перегибов, точек разрыва, особенностей поведения функции на бесконечности, специфики производных. Поэтому для сложных уравнений рекомендуется применять метод секущих или Больцано. Попытка преодолеть недостатки метода Ньютона осуществляется в методе Левенберга-Маркарда. Его идея заключается в том, что если точка очередного приближения попадет в область разрыва или экстремума и, следовательно, из нее нельзя будет провести направленную к корню касательную, то выбирается наиболее случайное число, которое прибавляется к координате приближения, и получается новое приближение, с высокой долей вероятности оказывающееся за пределами «опасной зоны». Этот метод является основным в MathCAD при использовании вычислительного блока Given/find.

В среде пакета Excel численные методы решения уравнений реализуются прямым применением описанных выше их алгоритмов, а также использованием специальных возможностей «Подбор параметров» или «Поиск решений».

Графическое решение уравнений.

Графическое решение уравнений с одной переменной заключается в определении одной координаты точки (или точек) пересечения графиков двух функций, соответствующих левой и правой частям уравнения.

Этот метод решения применяется в тех случаях, когда:

-решение нужно визуализировать;

-аналитическое решение невозможно из-за сложности уравнения;

-численное решение невозможно из-за дискретности входящих в уравнение функций.

В MathCAD и Excel метод реализуется имеющимися графическими средствами и операцией трассировки.

Аналитическое решение систем уравнений.

Традиционно системы уравнений делят на две группы: системы линейных уравнений (СЛУ) и системы нелинейных уравнений (СНУ), отличающиеся видом входящих в уравнение функций. В принципе линейные уравнения – не более чем подмножество нелинейных, поэтому способы решения СНУ вполне могут быть использованы для решения СЛУ. Однако в силу того, что на практике СЛУ приходится решать значительно чаще, им и методам их решения уделяют большее внимание.

Наиболее распространенные аналитические (точные) методы решения СЛУ (их еще называют прямыми или матричными) – это методы Гаусса, Крамера (или определителей) и обратной матрицы. Все они позволяют найти точные значения неизвестных после конечного числа арифметических операций, каждая из которых выполняется точно.

Метод Гаусса сводится к двум этапам. На первом (прямой ход) осуществляется приведением исходной системы уравнений с помощью преобразований к эквивалентной системе треугольного вида (с верхней треугольной матрицей). На втором этапе (обратный ход) находятся последовательно все переменные системы.

Метод Крамера требует вычисления определителей матриц, составленных из коэффициентов системы, и дальнейшей работы с ними.

Метод обратной матрицы предполагает решение системы, записанной в матричной форме, приемами линейной алгебры, в том числе использованием транспонирования, обращения матриц, при необходимости, разложения матриц по строкам или столбцам.

В тех случаях, если коэффициенты СЛУ очень отличаются друг от друга, эти методы могут давать погрешности в расчетах. Причем методы применимы только для хорошо определенных (совместных) СЛУ, где число уравнений равно числу неизвестных.

В MathCAD перечисленные методы реализуются либо непосредственным воспроизведением алгоритма, либо с помощью встроенных функций lsolve (метод Крамера) в комбинации с оператором символьного вывода или rref (метод Гаусса).В Excel наиболее просто реализуется алгоритм метода Гаусса.

Универсальных алгоритмов для поиска аналитических решений СНУ не существует. Поэтому при проведении ручного счета в этом случае используют математические преобразования, которые не всегда позволяют найти точные корни. В MathCAD аналитические решения СНУ можно искать с помощью оператора solve вычислительного блока Given/find в комбинации с оператором символьного вывода. В Excel аналитическое решение СНУ, как правило, не проводят.