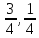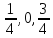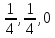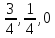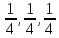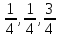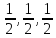- •3. Принцип плотнейшей упаковки. Одномерная и двумерная упаковки одинаковых шаров
- •4. Двухслойная и трехслойная упаковки одинаковых шаров в пространстве
- •5. Симметрия двухслойной и трехслойной плотнейших упаковок одинаковых шаров
- •6. Координаты шаров и пустот в двухслойной и трехслойной упаковках
- •7. Многослойные плотнейнше упаковки одинаковых шаров
5. Симметрия двухслойной и трехслойной плотнейших упаковок одинаковых шаров
Как двухслойная, так и трехслойная упаковки состоят из плотноупакованных слоев, обладающих симметрией p6mm, сдвинутых относительно друг друга. Следовательно, симметрию двухслойной и трехслойной упаковок можно получить, рассматривая процессы симметризации и диссимметризации при наложении друг на друга плотноупакованных слоев.
Буквенный символ двухслойной плотнейшей упаковки
… АВАВАВА... или … ВАВАВАВ …
инвариантен относительно зеркального отражения всей последовательности букв относительно плоскости симметрии, проходящей через любую букву А или В символа. Это значит, что вся бесконечная двухслойная плотнейшая упаковка одинаковых щаров инвариантна относительно зеркальных плоскостей симметрии, проходящих через слои А и В перпендикулярно осям 3-го порядка плотноупакованных слоев.
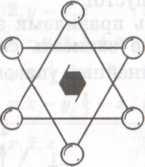
Сравним вид двухслойной упаковки на рис. 3 и график двумерной группы p6mm на рис.2. Основанием примитивной элементарной ячейки является ромб из четырех соседних шаров с углом при острой вершине 60°, ребра которого являются элементарными трансляциями, а и b. Трансляция с направлена перпендикулярно к плотноупакованным слоям. Ее длина равна расстоянию от первого до третьего слоя. С помощью несложного геометрического построения с учетом того, что параметр решетки а равен диаметру шара, а параметр с — удвоенной высоте тетраэдра (см. рис.5a), можно показать, что длина трансляции с относится к длине трансляции а (или b) как с/а = 2√2/3 ≈ 1,633...
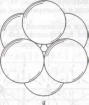
На рис.3 видно, что через каждую пустоту двухслойной упаковки проходит ось симметрии 3-го порядка. На рис. 8 изображены шесть шаров, которые образуют октаэдрическую пустоту. Нетрудно видеть, что три нижних и три верхних шара могут быть связаны комбинацией поворота на 60° и параллельного переноса на один слой вверх, т. е на половину трансляции с. Это означает, что кроме поворотной оси 3-го порядка через октаэдрические пустоты перпендикулярно к плотноупакованным слоям проходит трехзаходная винтовая ось 6-го порядка 63(z). Можно также заметить, что такая ось характерна не только для системы из шести шаров, образующих октаэдрическую пустоту, но и для всей двухслойной упаковки в целом.
Рассмотрим плоскости симметрии, характерные для двухслойной плотнейшей упаковки. Из сравнения рис.2 и 3 следует, что зеркальные плоскости, содержащие оси 3-го порядка и характерные для плотноупакованного слоя, присутствуют и в трехмерной двухслойной упаковке. Перемножая винтовой поворот 63(z) и зеркальные отражения в плоскостях симметрии, проходящих черезвинтовую ось, мы получим скользящие отражения в плоскостях типа с, параллельных винтовой оси. Например:
![]()
a b
Рис.8 . Шары, образующие октаэдрическую пустоту (о), и трехзаходная винтовая ось 6-го порядка в двухслойной плотнейшей упаковке одинаковых твердых шаров (б)
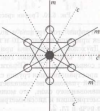
На рис.9 показано взаимное расположение зеркальных и скользящих плоскостей симметрии в двухслойной плотнейшей упаковке.
Умножая поворот вокруг винтовой оси 211(z), которая входит в состав оси 63, на отражение в плоскости mz, получим, что вся двухслойная упаковка инвариантна также относительно инверсии в точках на оси 63, смещенных относительно mz на с/4. Эти центры инверсии располагаются в геометрических центрах октаэдрических пустот.
Пользуясь
правилами записи обозначений
пространственных групп, можно записать
символ пространственной группы
двухслойной плотнейшей упаковки
одинаковых шаров как Р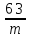 mc.
Полный график этой группы и полный набор
ее правильных систем точек приведен на
рис.10 и в табл.5.
mc.
Полный график этой группы и полный набор
ее правильных систем точек приведен на
рис.10 и в табл.5.
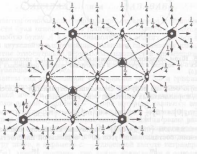
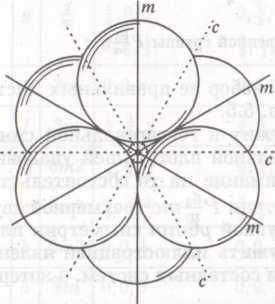
Рис.10
. График пространственной группы Р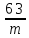 mc
mc
Двухслойная
упаковка принадлежит к гексагональной
сингонии, и ее часто называют гексагональной
плотнейшей упаковкой или сокращенно
ГПУ. Обратим внимание на то обстоятельство,
что пространственная группа симметрии
Р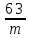 mc
трехмерной двухслойной упаковки не
совпадает с группой p6mm
симметрии плотноупакованного слоя, что
может служить иллюстрацией явлений
симметризации и диссимметризации
составных систем, о котором шла речь в
гл. 2.
mc
трехмерной двухслойной упаковки не
совпадает с группой p6mm
симметрии плотноупакованного слоя, что
может служить иллюстрацией явлений
симметризации и диссимметризации
составных систем, о котором шла речь в
гл. 2.
Обратимся к анализу симметрии трехслойной плотнейшей упаковки. Прежде всего заметим, что трехслойная упаковка так же инвариантна относительно осей 3-го порядка, как и плотноупакованный слой. В отличие от двухслойной упаковки, последовательности буквенных символов ... ABC ABC ABC..., равно как иэквивалентные последовательности ... СABCABCАВ... и ... СABCABCABC... не инвариантны относительно отражения, поэтому трехслойная упаковка не имеет плоскости симметрии, перпендикулярной осям 3-го порядка.
На рис. 11а показан фрагмент трехслойной упаковки; стрелкой показано направление, перпендикулярное к плотноупакованным слоям А, В и С. Из рисунка видно, что выделенный фрагмент инвариантен относительно оси 4-го порядка (показана нарис.11а квадратом).
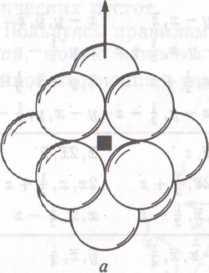

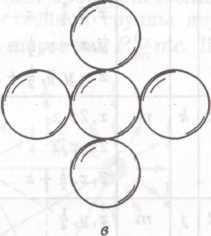
Рис.11 . Фрагмент трехслойной плотнейшей упаковки (а) и вид неплотноупакованных слоев, с помощью которых можно выложить трехслойную плотнейшую упаковку в направлении оси 4-го порядка (б, в)
Таблица5.
Правильные
системы точек пространственной группы
Р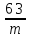 mc
mc
|
24 |
l |
1 |
x,y,z y̅,x-y,z y-x,x̅,z y̅,x̅,z
x,x-y,z
y-x,y,z
x̅,y̅,z̅
y,y-x,z̅
x-y,x,z̅
y,x,z̅
x̅,y-x,z̅
x-y,y̅,z̅
x̅,y̅, |
|
12 |
к |
т |
x,2x,z
2x̅,x̅,z
x,x̅,z
x̅,2x̅,z̅
2x,x,z̅
x̅,x,z̅
x̅,2x̅, |
|
12 |
j |
т |
x,y, |
|
12 |
i |
2 |
x,0,0
0,x,0
x̅,x̅,0
x,0, |
|
6 |
h |
тт |
x,2x, |
|
6 |
g |
|
|
|
4 |
е |
Зт |
0,0,
z
0,0,
z̅
0,0, |
|
4 |
f |
Зт |
|
|
2 |
d |
6m2 |
|
|
2 |
с |
6m2 |
|
|
2 |
b |
6m2 |
0,0, |
|
2 |
а |
3m |
0,0,0
0,0, |
Показанная часть упаковки полностью окружает (координирует) центральный шар. Поэтому, если принять, что все шары упаковки симметрично эквивалентны, то мы придем к выводу, что ось 4-го порядка характерна для всей рассматриваемой упаковки. Наличие осей 3-го порядка и 4-го порядка сразу же позволяет отнести трехслойную плотнейшую упаковку одинаковых шаров к кубической сингонии. Поэтому данную упаковку часто называют кубической упаковкой.
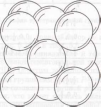
Рис.12. Фрагмент трехслойной плотнейшей упаковки, образованной с помощью неплотноупакованных слоев квадратной упаковки
Рассмотрим трехслойную упаковку в несколько ином аспекте. Из рис.11б видно, что в направлении, перпендикулярном оси 4-го порядка, данную упаковку можно представить в виде совокупности неплотноупакованных слоев двух видов. Если обозначить слои, показанные на рис.11б, буквой а, а слои на рис.11в буквой β, то трехслойную плотнейшую упаковку можно выложить слоями ... αβαβαβ... Такие неплотные упаковки на плоскости обычно называют квадратными. Заметим, что при создании трехслойной плотнейшей упаковки неплотноупакованные слои α и β укладываются «плотно», т. е. так, чтобы каждый шар касался 12-ти соседей.
На рис.12 приведен фрагмент βαβ трехслойной плотнейшей упаковки. Здесь явно видна кубическая симметрия упаковки, причем можно сразу обнаружить наличие плоскостей симметрии,
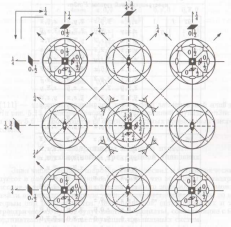
Рис.13. График пространственной группы симметрии Fm3m:
Показана одна четвертая часть полного графика группы
что позволяет отнести пространственную группу симметрии кубической плотнейшей упаковки к классу Оh. Более того, приведенный фрагмент представляет собой кубическую элементарную ячейку, отвечающую гранецентрированной решетке с симморфной пространственной группой Fm3m. Плотноупакованные слои на этом рисунке располагаются перпендикулярно направлениям {111] — телесным диагоналям кубической элементарной ячейки. На рис.13 приведен график пространственной группы Fm3m, а в табл.6 — координаты ее общих и частных правильных систем точек.
Таблица 6. Правильные системы точек пространственной группы Fm3m
|
192 |
l |
1 |
x,y,z x̅,y̅,z x̅,y,z̅ x,y̅,z̅ z,x,y z,x̅,y̅ z̅,x̅,y z̅,x,y̅ y,z,x y̅,z,x̅ y,z̅,x̅ y̅,z̅,x y,x,z̅ y̅,x̅,z̅ y,x̅,z y̅,x,z x,z,y̅ x̅,z,y x̅,z̅,y̅ x,z̅,y z,y,x̅ z,y̅,x z̅,y,x z̅,y̅,x̅ x̅,y̅,z̅ x,y,z̅ x,y̅,z x̅,y,z z̅,x̅,y̅ z̅,x,y z,x,y̅ z,x̅,y y̅,z̅,x̅ y,z̅,x y̅,z,x y,z,x̅ y̅,x̅,z y,x,z y̅,x,z̅ y,x̅,z̅ x̅,z̅,y x,z̅,y̅ x,z,y x̅,z,y̅ z̅,y̅,x z̅,y,x̅ z,y̅,x̅ z,y,x |
|
96 |
k |
m |
x,x,z x̅,x̅,z x̅,x,z̅ x,x̅,z̅ z,x,x z,x̅,x̅ z̅,x̅,x z̅,x,x̅ x,z,x x̅,z,x̅ x,z̅,x̅ x̅,z̅,x x,x,z̅ x̅,x̅,z̅ x,x̅,z x̅,x,z x,z,x̅ x̅,z,x x̅,z̅,x̅ x,z̅,x z,x,x̅ z,x̅,x z,x,x z̅,x̅,x̅ |
|
96 |
j |
m |
0,y,z 0,y̅,z 0,y,z̅ 0,y̅,z̅ z,0,y z,0,y̅ z̅,0,y z̅,0,y̅ y,z,0 y̅,z,0 y,z̅,0 y̅,z̅,0 y,0,z̅ y̅,0,z̅ y,0,z y̅,0,z 0,z,y̅ 0,z,y 0,z̅,y̅ 0,z̅,y z,y,0 z,y̅,0 z̅,y,0 z̅,y̅,0 |
|
48 |
i |
mm2 |
y, y,y, |
|
48 |
h |
mm2 |
0,y,y 0,y̅,y 0,y,y̅ 0,y̅,y̅ y,0,y y,0,y̅ y̅,0,y y̅,0,y̅ y,y,0 y̅,y,0 y,y̅,0 y̅,y̅,0 |
|
48 |
g |
mm2 |
x,
x, |
|
32 |
f |
3m |
x,x,x x̅,x̅,x x̅,x,x̅ x,x̅,x̅ x,x,x̅ x̅,x̅,x̅ x,x̅,x x̅,x,x |
|
24 |
e |
4mm |
x,0,0 x̅,0,0 0,x,0 0,x̅,0 0,0,x 0,0,x̅ |
|
24 |
d |
mmm |
0,
|
|
8 |
c |
4̅3m |
|
|
4 |
b |
m3m |
|
|
4 |
a |
m3m |
0,0,0 |

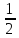 +z
y,y-x,
+z
y,y-x,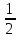 +z
x-y,x,
+z
x-y,x, +
z
x,y,
+
z
x,y,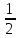 -z
y̅,x-y,
-z
y̅,x-y,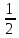 -z
y-x,x̅,
-z
y-x,x̅,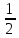 -z
y,x,
-z
y,x,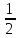 +z
x̅,y-x,
+z
x̅,y-x,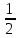 +z
x-y,y̅,
+z
x-y,y̅,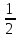 +z
y̅,x̅,
+z
y̅,x̅,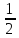 -z
x,x-y,
-z
x,x-y,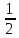 –z
y-x,y,
–z
y-x,y, -z
-z +z
2x,x,
+z
2x,x,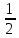 +z
x̅,x,
+z
x̅,x,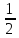 +z,
x,2x,
+z,
x,2x,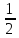 -z
2x̅,x̅
-z
2x̅,x̅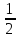 -z
x,x̅,
-z
x,x̅,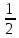 -z
-z y̅,x-y,
y̅,x-y,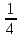 y-x,x̅,
y-x,x̅,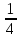 y̅,x̅,
y̅,x̅,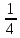 x,x-y,
x,x-y,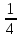 y-x,y,
y-x,y,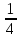 x̅,y̅,
x̅,y̅,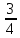 y,y-x,
y,y-x,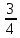 x-y,x,
x-y,x,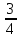 y,x,
y,x, x̅,y-x,
x̅,y-x,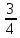 x-y,y̅,
x-y,y̅,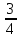
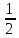 0,x,
0,x,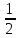 x̅,
x̅,
x̅,
x̅, x̅,0,0
0,x̅,0
x,x,0
x̅,0,
x̅,0,0
0,x̅,0
x,x,0
x̅,0,
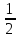 0,x,
0,x,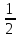 x,x,
x,x,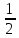
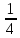 2x̅,x̅,
2x̅,x̅, x,x̅,
x,x̅,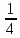 ,x̅,2x̅,
,x̅,2x̅,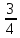 2x,x,
2x,x,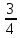 x̅,x,
x̅,x,
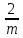
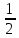 ,0,0
0,
,0,0
0,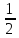 ,0
,0
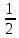 ,
, ,0
,0
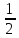 ,0,
,0,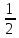 0,
0, ,
,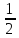
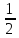 ,
,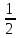 ,
,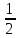
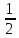 +z
0,0,
+z
0,0, -z
-z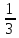 ,
,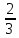 ,z
,z
 ,
,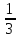 ,
z̅
,
z̅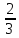 ,
,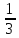 ,
,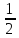 +z
+z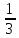 ,
,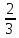 ,
,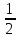 -z
-z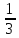 ,
,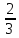 ,
,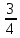
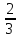 ,
,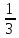 ,
,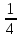
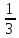 ,
,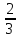 ,
,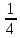
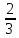 ,
,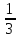 ,
,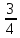
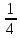 0,0,
0,0,
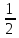
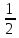 ,y,y
,y,y
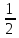 ,y̅,y
,y̅,y ,y,y̅
,y,y̅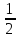 ,y̅,y̅
,y̅,y̅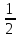 ,y
y,
,y
y, ,y̅
y̅,
,y̅
y̅, ,y
y̅,
,y
y̅, ,y̅
,y̅ y̅,y,
y̅,y, y,y̅,
y,y̅, y̅,y̅,
y̅,y̅,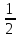
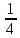 ,
,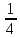 x̅,
x̅,
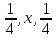
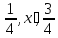
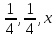
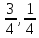 ,
x̅
,
x̅

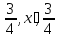
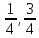
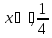 ,
,
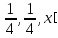
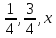
 ,
,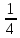 0,
0,