Обратные матрицы. (Возвращение в линейную алгебру)

Пусть дана квадратная матрица А

aij – минор 1ого порядка

Mij– дополнительный минор порядка (n-1)

Aij=(-1) ∙Mij – алгебраическое дополнение для aij

Определитель 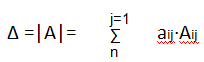(где i-фиксированно)

Матрица B называется обратной матрицей по отношению к A, если A*B=B*A=E(единичная матрица).

Замечание: Обратная матрица для квадратной матрицы В, имеет тот же порядок, что и исходная, если она существует.

Теорема:

Всякая невырожденная квадратная матрица любого порядка имеет обратную:

-ассоциированная матрица (присоединенная).

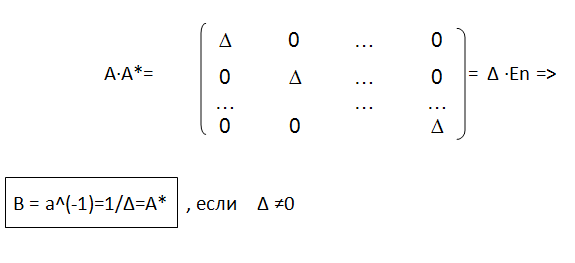
Вспомним,

1. a □ (b□c)=(a□b) □c

2. Ǝ z є V | ∀ a є V |a□z=z□a=a

3. ∀ a Ǝ n | n□a=a□n=z

4. a□b=b□a

5. (α+β) ∆ a=( α∆a)□( β∆a)

6. α∆ (a□b)= (α∆ a) □( α∆ b)

7. α∆ (β ∆ a)= (αβ )∆ a

8.1∆ a=a

∀ a, b є V; α,β є P; 1 є P

Система векторов, состоящая из хотя бы одного вектора:

1. A1=(ā)- линейно зависима ↔ ā =0

b=λ ā, так как ā =0, то b=0, значит A1=( ā) – линейно зависима

2. А1=(ā)-линейно независима ↔а≠0

По определению b=0;

b=λa , так как a≠0, то λ =0, значит A1=(a) – линейно независима.

3. А2=( ā1, ā2)-линейно зависима↔ ā1|| ā2, то вектор а линейно выражается через ā2, следовательно, по критерию линейной зависимости А2=( ā1, ā2) –линейно зависима.

4. А2=( ā1, ā2)-линейно-независима↔ ā1|| ā2

ā1|| ā2→ ā1-линейно не выражается через ā2, значит А2-линейно-независима

Теорема: Определитель произведения двух квадратных матриц равен произведению их определителей.

|АВ|=|А|∙|В|

А=(aij), mxn

B=(bij),mxn

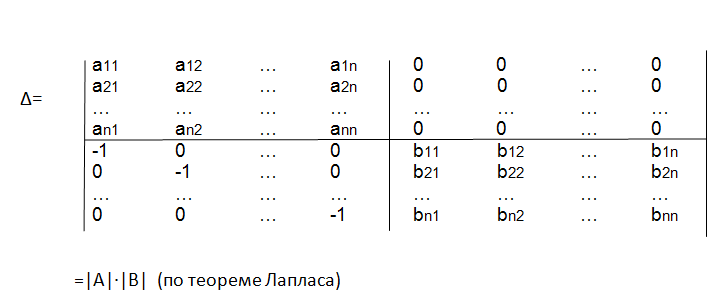
Преобразуем определитель так, чтобы в правом нижнем углу были «0» ,но чтобы величина определителя не менялась.

S=(1+2+…+n)+(n+1+n+2+…+n+n)=2(1+2+n)+n∙n

(-1)^(n+s)=2n(n+1)+n+n^2=2n(n+1)

Теорема: «Необходимое условие существования матрицы»

Для того чтобы квадратная матрица А имела обратную матрицу , она не должна быть невырожденная.

Доказательство:

Пусть есть обратная матрица А^(-1)

A∙A^(-1)=A∙(-1) ∙A=E(по определению)

По предыдущей теореме переходим к:

|A|∙|A^(-1)|=|E|=1 → |A|≠0

Теорема: Пересечение двух подпространств является подпространством.

Дано: V-векторное пространство, L1, L2 є V

L1 подпространство пространства V Это означает:

1. ā1, ā2 є L → ā1 + ā2 є L1

2. ∀ числа λ и ∀ ā1 є L1 → λ∙ ā1 є L1

(замкнутость относительно линейных операций)

Доказательство:

Берем L1 ∩ L2 = L

1. ā1, ā2 є L → ā1, ā2 є L 1 и ā1, ā2 є L 2

→ ā1 + ā2 є L1 и ā1 + ā2 є L2 → ā1+ ā2 є L2 → ā1 + ā2 є L1→ ā1 + ā2 є L → L1 ∩ L2

2. ∀ числа λ и ∀ ā1 є L1

λ∙ ā1 є L1 и λ∙ ā1 є L1 → λ∙ ā1 є L

Сумма двух подпространств.

V, lim V=n

L1, L2 є V

Подпространство L= L1+ L2 =(def)={ӯ1=ā1 + ā2 | ā1 є L 1, ā2 є L2 }

Доказательство:

ӯ1, ӯ2 є L1 + L2 ↔ ӯ1=ā1 + ā2 и ӯ2=ā3 + ā4

ā1, ā3 є L 1, ā2, ā4 є L2

1. ӯ1+ ӯ2= (ā1 + ā2) + (ā3 + ā4)= (ā1 + ā3) + (ā2 + ā4)

є L 1 є L2

2. ∀ числа λ и ∀ ӯ 1 є L | λ∙ ӯ= λ∙( ā1 + ā2)= λ∙ā1+ λ∙ ā2= L1 + L2

є L 1 є L2

Векторное пространство

Теорема о пополнение

Пусть V - векторное пространство dimV=n( ∃ базис ē₁ ,ē₂ , … ,ē_n). ∀ линейно-независимую упорядоченную систему векторов ( ƒ̅ ₁ ,ƒ̅₂ , … , ƒ̅_n )⊂ V можно дополнить до некоторого базиса пространства V. В частности ∀ не нулевой вектор V можно включить в некоторый базис.

Если s=n, то это уже базис.

Если s>n быть не может, потому что в ∀ системе векторов больше, чем в базисе – она линейно зависима.

Если s<n :

(1) ƒ̅ ₁, ƒ̅₂, … , ƒ̅_s, ē₁, ē₂ , … ,ē_n – (n+s) векторов. Отбросим все векторы, которые выражаются через предыдущие. Так как F_s линейно независима, то она остается, по критерию линейно независимости.

2. ƒ̅ ₁, ƒ̅₂, … , ƒ̅_s, ē_𝑖1, ē_𝑖2 , … ,ē_𝑖𝑛 составим произвольную линейную комбинацию

α₁ƒ̅ ₁, α₂ ƒ̅₂, … , α_s ƒ̅_s, β₁ē_𝑖1, β₂ē_𝑖2 , … ,β_k ē_𝑖n

β_n с максимальным n, β_n≠0 ⇒ ē_𝑖n выражается через предыдущий ⇒ β_n=0

α₁ƒ̅ ₁+ α_s ƒ̅_s=ō ⇒ α₁,α₂,… ,α_s=0

Значит, наша система 2 линейно независима.

2 – полная система, так как ∀ вектор пространства V линейно выражается через систему 1, через 2в силу транзетивности: линейный вектор пространства V выражается через систему 2.

Следствия:

Если есть подпространство пространства, то размерность подпространства не превосходит размерность пространства: L⊂V ⇒ dimL≤dimV

dimL=dimV ⇒ L=V

Базис любого подпространства можно включить в некоторый базис объемлющего пространства.

Сумма подпространств.

Сумма подпространств – это такое множество, которое состоит из элементов одного и другого подпространств

Теорема. Размерность суммы.

Пусть U и W –конечномерные подпространства V.

dim(U+W) = dimU + dimW - dimU∩W

k = dimU p=dimW m = dimU∩W

U∩W⊂U ⇒ m ≤ k

U∩W⊂W ⇒ m ≤ p

В пересечение подпространств выбираем какой либо базис

ē₁, ē₂ , … ,ē_m( базис U∩W) a̅₁, …, a̅_k-m-базис в U

ē₁, ē₂ , … ,ē_m( базис U∩W) b̅₁,…,b̅̅_p-m базис в W

z = u + w u∊U,w∊W

u+w=[ ē₁, ē₂ , … ,ē_m, a̅₁, …, a̅_k-m, b̅₁,…,b̅̅_p-m] – линейная оболочка.

Любой вектор суммы принадлежит линейной оболочке.

Осталось проверить линейную независимость.

Равенство нулю возможно только в тривиальном случае.

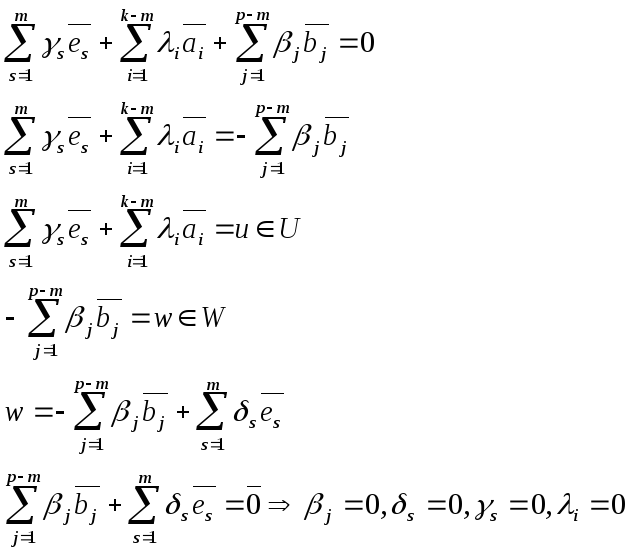
Прямая сумма.

Определение.L₁ L₂ – Подпространства из V.

dim(L₁+L₂) = dimL₁ + dimL₂ – dim(L₁∩L₂)

L₁+L₂ – называется прямой суммой, если для любого вектора а̅ ∊ L₁+L₂ | а̅ ∊ = а̅₁ + а̅₂ однозначно, где а̅_𝑖 ∊ L_𝑖

Если L₁∩L₂ = {0}-дизъюнктные подпространства.

Теорема.

L₁+L₂ –Прямая сумма тогда, и только тогда, когда L₁ и L₂ - дизъюнктны.

Доказательство:

Пусть L₁+L₂ прямая сумма тогда, и только тогда, когда ∀а̅ ∊ L₁+L₂⃒ а̅ = а̅̅₁+а̅₂ ⃒b̅ ∊ L₁∩L₂ ∼ b̅∊ L₁, b̅∊ L₂⇒ а̅ = (а̅̅₁+ b̅) + (а̅̅₁- b̅) – однозначно (а̅_𝑖 ∊ L_𝑖)⇒ сумма прямая ⇔ пересечение нулевое.

Понятие как суммы, так прямой суммы, распределяются на любое число слагаемых.

L₁⊕L₂ – обозначение прямой суммы (внутренняя прямая сумма).

Внешняя прямая сумма.

Пусть заданы два векторных пространства L₁ и L₂.

V = L₁𝗑 L₂ – декартого произведение.

𝒰,𝒱 ∊ V = L₁𝗑 L₂

𝒰 =(𝒰₁,𝒰₂) ⃒ 𝒰_𝑖∊ L_𝑖

𝒱=(𝒱₁,𝒱₂) ⃒ 𝒱_𝑖∊ L_𝑖

𝒰+𝒱=(𝒰₁,𝒰₂)+(𝒱₁,𝒱₂)≝( 𝒰₁+𝒱₁,𝒰₂+𝒱₂).

∀ λ – число λV = λ(V₁,V₂)≝(λV₁,λV₂)

V₁={V=(V₁,0)∊V}≡ L₁𝗑{0} – пластина произведения L₁𝗑 L₂ параллельная L₁

V₂={V=(0,V₂)∊V}≡ L₂𝗑{0} – пластина произведения L₁𝗑 L₂ параллельная L₂

V₁ ≌ L₁, V₂ ≌ L₂ , V≌ L₁⊕L₂ – внешняя прямая сумма.

Критерии базисов.

Пусть дано векторное пространство векторов V конечномерное

dimV = n

∀ dimV = n (∃ базис ē₁, ē₂ , … ,ē_n)

𝒜 _n=(𝑎̅₁,𝑎̅₂, …, 𝑎̅_n).