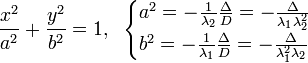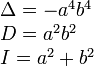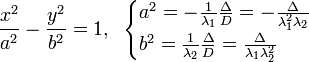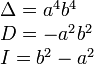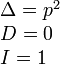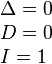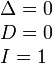- •Глава I. Множества, отображения и функции
- •Глава II. Введение в теорию векторных пространств.
- •1. Множества, отображения и функции
- •1.1. Множества. Общие понятия
- •1.2. Числовые множества.
- •1.3. Отображения
- •1.4. Композиция отображений. Обратные отображения.
- •2. Геометрические векторы. Основные определения
- •2. Простейшие операции над векторами
- •Числовые матрицы.
- •Определитель матрицы.
- •1. Понятие определителя
- •2. Правило Сарруса для квадратных матриц 3 порядка.
- •3. Свойства определителей
- •1. Равноправность строк и столбцов.
- •2. Антисимметрия при перестановке двух строк.
- •3. Линейное свойство определителя.
- •Обратные матрицы. (Возвращение в линейную алгебру)
- •Сумма двух подпространств.
- •1 Критерий базиса.
- •3Критерий базиса.
- •Замена базиса и преобразование координат векторов при замене базиса.
- •Матрица гомоморфизма. Координатная запись гомоморфизма.
2. Правило Сарруса для квадратных матриц 3 порядка.
Определителем матрицы третьего порядка, или определителем третьего порядка, называется число, которое вычисляется по формуле:
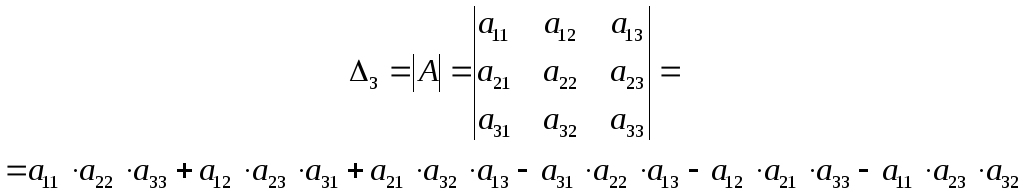
Это число представляет алгебраическую сумму, состоящую из шести слагаемых. В каждое слагаемое входит ровно по одному элементу из каждой строки и каждого столбца матрицы. Каждое слагаемое состоит из произведения трех сомножителей.

Знаки, с которыми члены определителя входят в формулу нахождения определителя третьего порядка можно определить, пользуясь приведенной схемой, которая называется правилом треугольников или правилом Сарруса. Первые три слагаемые берутся со знаком плюс и определяются из левого рисунка, а последующие три слагаемые берутся со знаком минус и определяются из правого рисунка.
Пример. Вычислить определитель третьего порядка:
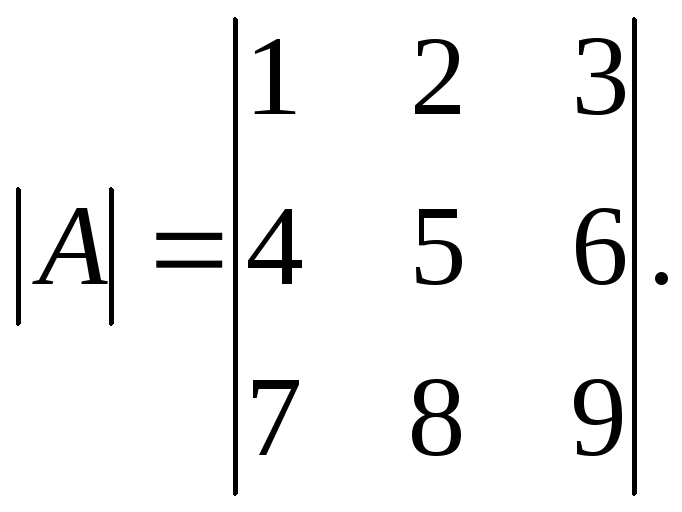
Решение.
![]()
3. Свойства определителей
Рассмотрим ряд свойств, которыми обладают определители.
1. Равноправность строк и столбцов.
Определение 1. Транспонированием определителя называется операция, в результате которой меняются местами строки и столбцы с сохранением порядка их следования.
Определитель,
полученный в результате транспонирования,
называется транспонированным по
отношению к исходному и обозначается
![]() .
.
Свойство
1. При
транспонировании величина определителя
сохраняется, то есть
![]() .
.
Доказательство этого свойства вытекает из того, что разложение определителя по первой строке тождественно совпадает с разложением по первому столбцу. Данное свойство указывает на равноправность строк и столбцов, поэтому все дальнейшие свойства можно рассматривать лишь для строк.
2. Антисимметрия при перестановке двух строк.
Свойство 2. При перестановке местами двух строк определитель сохраняет свою абсолютную величину, но меняет знак на противоположный.
Докажем для определителя второго порядка. Действительно,
![]() ;
;
![]() .
.
Для
определителя
![]() -го
порядка докажем это свойство по индукции.
Пусть свойство справедливо для
определителя
-го
порядка докажем это свойство по индукции.
Пусть свойство справедливо для
определителя![]() -го
порядка. Разложим определитель
-го
порядка. Разложим определитель![]() -го
порядка по любой строке, отличной от
переставленных. Тогда переставленные
строки входят во все миноры, на которые
умножаются элементы
-го
порядка по любой строке, отличной от
переставленных. Тогда переставленные
строки входят во все миноры, на которые
умножаются элементы![]() ,
но эти миноры являются определителями
,
но эти миноры являются определителями![]() -го
порядка и меняют свой знак при перестановке
строк. Следовательно, и определитель
-го
порядка и меняют свой знак при перестановке
строк. Следовательно, и определитель![]() -го
порядка также меняет свой знак.
-го
порядка также меняет свой знак.
3. Линейное свойство определителя.
Определение
2. Некоторая
строка (![]() )
является линейной комбинацией строк
(
)
является линейной комбинацией строк
(![]() )
и (
)
и (![]() )
с коэффициентами
)
с коэффициентами![]() и
и![]() ,
если
,
если![]() .
.
Пользуясь этим определением, перейдем к самому свойству.
Свойство
3. Если
в определителе
![]() -го
порядка
-го
порядка![]() некоторая строка
некоторая строка![]() (
(![]() )
является линейной комбинацией двух
строк (
)
является линейной комбинацией двух
строк (![]() )
и (
)
и (![]() )
с коэффициентами
)
с коэффициентами![]() и
и![]() ,
то
,
то![]() ,
где
,
где![]() - определитель, у которого
- определитель, у которого![]() -ая
строка равна (
-ая
строка равна (![]() ),
а все остальные - те же, что и у
),
а все остальные - те же, что и у![]() ,
а
,
а![]() - определитель, у которого
- определитель, у которого![]() -ая
строка равна (
-ая
строка равна (![]() ),
а все остальные - те же, что и у
),
а все остальные - те же, что и у![]() .
.
Для
доказательства разложим каждый из
определителей по
![]() -ой
строке. Очевидно, что у всех разложений
миноры
-ой
строке. Очевидно, что у всех разложений
миноры![]() соответствующих элементов будут
одинаковы. Вычислим
соответствующих элементов будут
одинаковы. Вычислим![]() :
:
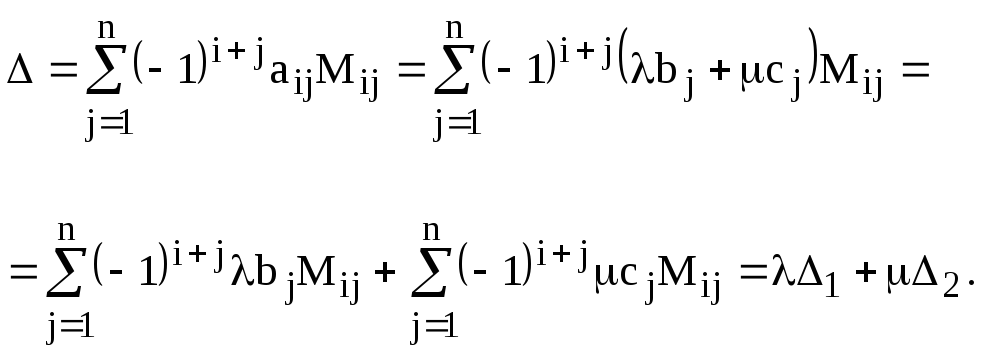
Итак, свойство доказано. Очевидно, оно справедливо и для столбцов.
Приведенные три свойства называются основными. Остальные являются их следствиями.
Свойство
4. Умножение
всех элементов некоторой строки или
столбца определителя на число
![]() равносильно умножению определителя на
число
равносильно умножению определителя на
число![]() .
.
Для
доказательства положим в свойстве 3
![]() ,
тогда получим
,
тогда получим![]() .
Значит, общий множитель всех элементов
некоторого ряда можно выносить за
определитель.
.
Значит, общий множитель всех элементов
некоторого ряда можно выносить за
определитель.
Свойство 5. Если все элементы некоторой строки или столбца определителя равны 0, то и сам определитель равен 0.
Для доказательства разложим определитель по нулевому ряду.
Свойство 6. Определитель с двумя равными строками или столбцами равен 0.
Действительно,
переставив местами равные строки или
столбцы, получим тот же определитель,
но по свойству 2 его знак изменится на
противоположный. Итак, с одной стороны
![]() ,
а с другой
,
а с другой![]() .
Следовательно,
.
Следовательно,![]() .
.
Свойство 7. Если соответствующие элементы двух строк или столбцов определителя пропорциональны, то определитель равен нулю.
Действительно, согласно свойству 4 общий множитель можно выносить за определитель, и мы получим определитель с двумя равными строками, который по свойству 6 равен нулю.
Свойство
8. Если
к элементам некоторой строки или столбца
определителя прибавить соответствующие
элементы другой строки или столбца,
умноженные на произвольный множитель
![]() ,
то величина определителя не изменится.
,
то величина определителя не изменится.
Доказательство.
Рассмотрим определитель
![]() .
Прибавим к элементам второй строки
элементы первой с коэффициентом
.
Прибавим к элементам второй строки
элементы первой с коэффициентом![]() :
:
![]() .
.
Тогда, по свойству 3 получим:
![]() .
.
После перечисления всех свойств определителей введем еще одно определение.
Определение
3. Алгебраическим
дополнением данного элемента
![]() определителя
определителя![]() -го
порядка называется число, равное
-го
порядка называется число, равное![]() ,
которое обозначается
,
которое обозначается![]() .
.
Значит, алгебраическое дополнение отличается от соответствующего минора только лишь знаком. Теперь величину определителя можно вычислить с помощью формул:
![]() .
.
Пользуясь свойствами, любой определитель можно вычислить не на основании основного правила, а предварительно упростив его (приводя, например, к треугольному виду).
СЛАУ.
Рассмотрим систему линейных алгебраических уравнений (СЛАУ) относительно n неизвестных x1 , x2 , ..., xn:
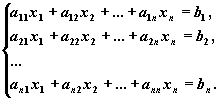
Эта система в "свернутом" виде может быть записана так:
ni=1aij xj = bi , i=1,2, ..., n.
В соответствии с правилом умножения матриц рассмотренная система линейных уравнений может быть записана в матричной форме Ax=b, где
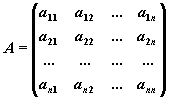 ,
,
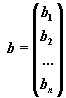 ,
,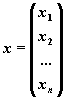 .
.
Матрица A, столбцами которой являются коэффициенты при соответствующих неизвестных, а строками - коэффициенты при неизвестных в соответствующем уравнении называется матрицей системы. Матрица-столбец b, элементами которой являются правые части уравнений системы, называется матрицей правой части или просто правой частью системы. Матрица-столбец x, элементы которой - искомые неизвестные, называется решением системы.
Система линейных алгебраических уравнений, записанная в виде Ax=b, является матричным уравнением.
Если матрица системы невырождена, то у нее существует обратная матрица и тогда решение системы Ax=b дается формулой:
x=A -1 b.
Справедливо следующее утверждение (формулы Крамера).
Если определитель D=det A матрицы системы Ax=b отличен от нуля, то система имеет единственное решение x1 , x2 , ..., xn, определяемое формулами Крамера
xi =Di / D, i=1,2, ..., n,
где Di - определитель матрицы n -го порядка, полученной из матрицы A системы заменой i -го столбца столбцом правых частей b.
Пример. Вычисление решения системы линейных уравнений по формулам Крамера.
Решить систему:

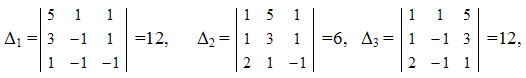 х1
= 12/6=2, х2
=
6/6=1, х3
= 12/6=2.
х1
= 12/6=2, х2
=
6/6=1, х3
= 12/6=2.
Метод Гаусса применим для решения системы линейных алгебраических уравнений c невырожденной матрицей системы. Идея метода Гаусса состоит в том, что систему n линейных алгебраических уравнений относительно n неизвестных x1 , x2 , ..., xn
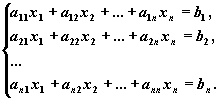
приводят последовательным исключением неизвестных к эквивалентной системе с треугольной матрицей
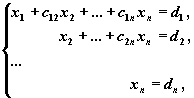
решение которой находят по рекуррентным формулам:
xn =dn , xi = di -S nk=i+1 cik xk , i=n-1, n-2, ...,1.
Матричная запись метода Гаусса.
Прямой ход метода Гаусса: приведение расширенной матрицы системы
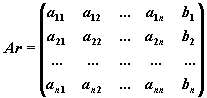 к
ступенчатому виду
к
ступенчатому виду
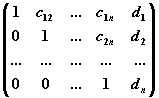 с
помощью элементарных
операций над строками
матрицы (под элементарными операциями
понимаются следующие операции:
с
помощью элементарных
операций над строками
матрицы (под элементарными операциями
понимаются следующие операции:
перестановка строк;
умножение строки на число, отличное от нуля;
сложение строки матрицы с другой строкой, умноженной на отличное от нуля чиcло).
Обратный
ход
метода Гаусса: преобразование полученной
ступенчатой матрицы к матрице, в первых
n
столбцах которой содержится единичная
матрица
 ,
последний,(n+1)-й,
столбец этой матрицы содержит решение
системы.
,
последний,(n+1)-й,
столбец этой матрицы содержит решение
системы.
Пример. Решить систему уравнений методом Гаусса.
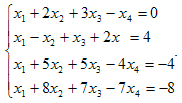
Решение:
Выписав расширенную матрицу этой системы, после ряда элементарных преобразований (проследить порядок которых рекомендуем самостоятельно), получим:
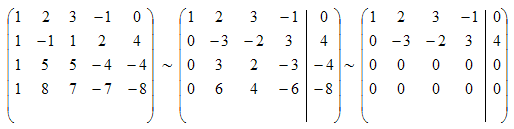
откуда
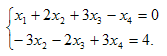
Решая последнюю систему, находим
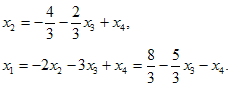
Здесь ранг расширенной матрицы равен рангу основной матрицы и равен, очевидно, двум. Система имеет бесконечно много решений, каждое из которых можно получить, придавая х3 и х4 конкретные значения.
Кривые второго порядка
Опр.
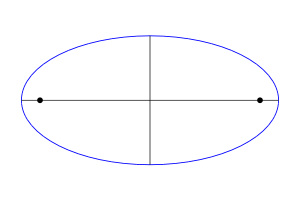
Это такое геометрическое место точек на плоскости, уравнение которого имеет вид:
![]() (1)
(1)
в
котором, по крайней мере один из
коэффициентов
![]() отличен
от нуля.
отличен
от нуля.
![]() -
числа коэффициенты
-
числа коэффициенты
![]()
![]() ,
,
![]()
Три замечательных кривых
Эллипс
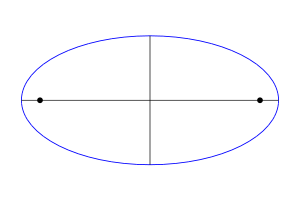
Эллипс, его фокусы и главные оси
Геометрическое
место точек в плоскости {Э}, сумма
расстояний от каждой из которых до двух
фиксированных точек F1
и F2
плоскости, называемых фокусами есть
величина постоянная равная
![]()
Э - эллипс
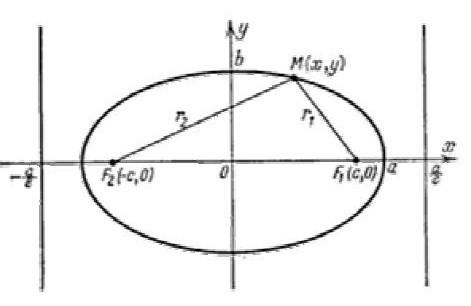
Каноническое уравнение эллипса:
![]() ,
где
,
где
![]()
Эксцентриситет
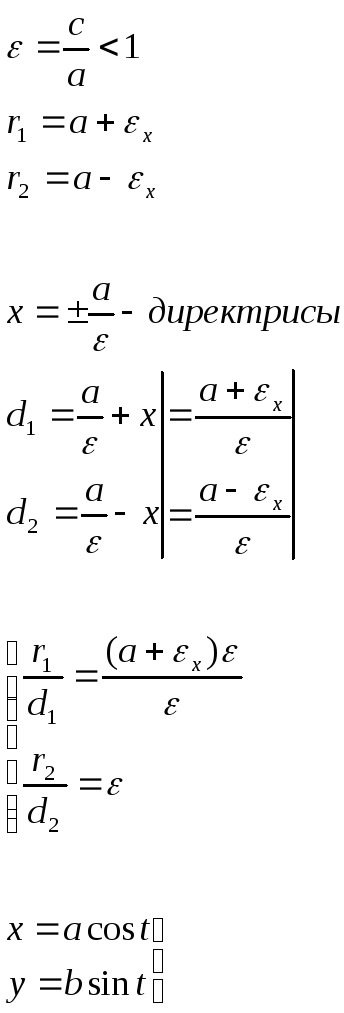 параметрическое
уравнение эллипса
параметрическое
уравнение эллипса
заменим, и получим каноническое уравнение эллипса
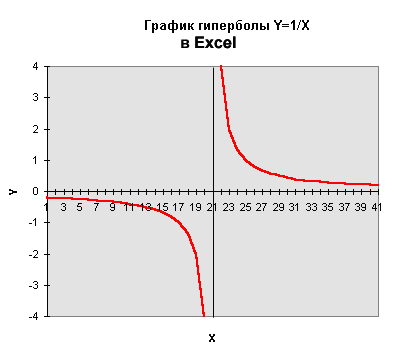
Гипербола
Называется геометрическое место точек плоскости, абсолютная величина разности расстояний от каждой из которых до двух фиксированных точек этой плоскости (называемых фокусами) есть величина постоянная, она меньше расстояний между фокусами.
Г - гипербола
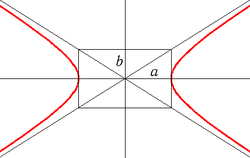
Гипербола, её полуоси и асимптоты
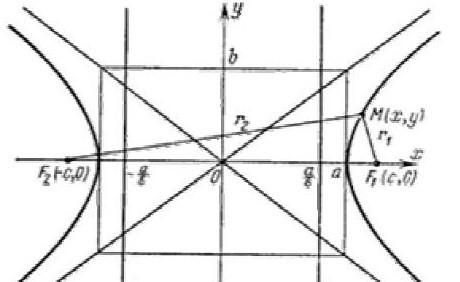
Осью гиперболы называется прямая, соединяющая её фокусы.
Расстояние от начала координат до одного из фокусов гиперболы называют фокусным расстоянием гиперболы
 .
.Расстояние от начала координат до одной из вершин гиперболы называется большой или вещественной полуосью гиперболы
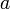 .
.Расстояние от вершины гиперболы до асимптоты вдоль направления параллельного оси ординат называется малой или мнимой полуосью гиперболы
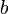 .
.Отношение фокусного расстояния к большой полуоси гиперболы называется эксцентриситетом:
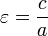 .
Эксцентриситет гиперболы всегда больше
единицы.
.
Эксцентриситет гиперболы всегда больше
единицы.Расстояние от фокуса до гиперболы вдоль прямой, параллельной оси ординат называется фокальным параметром
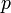 ..
..
M(x, y) r1 r2 x F1 a F2
По определению r1 – r2= 2a. F1, F2 – фокусы гиперболы. F1F2 = 2c. Выберем на гиперболе произвольную точку М(х, у).
Тогда:

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
обозначим с2
– а2
= b2
(геометрически эта величина – меньшая
полуось)
![]() =
=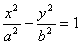
Получили каноническое уравнение гиперболы. Гипербола симметрична относительно середины отрезка, соединяющего фокусы и относительно осей координат. Ось 2а называется действительной осью гиперболы.
Ось 2b
называется мнимой осью гиперболы.
Гипербола имеет две асимптоты, уравнения
которых
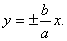
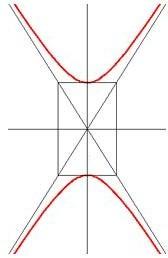
Сопряженная гипербола
Парабола
Параболой называется геометрическое место точек плоскости, для каждой из которых расстояние до фиксированной точки этой плоскости, называемой фокусом, равно расстоянию до фиксированной прямой, лежащей в той же плоскости и называемой директрисой параболы.
Чтобы
получить уравнение кривой, соответствующей
этому определению, введем подходящую
систему координат. Для этого из фокуса
![]() опустим
перпендикуляр
опустим
перпендикуляр![]() на
директрису
на
директрису![]() .
Начало координат
.
Начало координат![]() расположим
на середине отрезка
расположим
на середине отрезка![]() ,
ось
,
ось![]() направим
вдоль отрезка
направим
вдоль отрезка![]() так,
чтобы ее направление совпадало с
направлением вектора
так,
чтобы ее направление совпадало с
направлением вектора![]() .
Ось
Oy проведем
перпендикулярно оси
.
Ось
Oy проведем
перпендикулярно оси
![]()
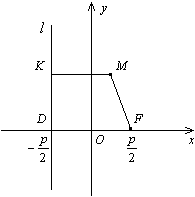
Пусть
расстояние между фокусом
![]() и
директрисой
и
директрисой![]() параболы
равноp.
Тогда в выбранной системе координат
парабола имеет уравнение
параболы
равноp.
Тогда в выбранной системе координат
парабола имеет уравнение
|
|
(*) |
Доказательство.
В выбранной системе координат фокусом
параболы служит точка
![]() ,
а директриса имеет уравнение
,
а директриса имеет уравнение![]()
Пусть
![]() --
текущая точка параболы. Тогда по
формуле для плоского случая находим
--
текущая точка параболы. Тогда по
формуле для плоского случая находим
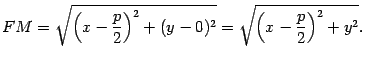
Расстоянием
от точки
![]() до
директрисы
до
директрисы![]() служит
длина перпендикуляра
служит
длина перпендикуляра![]() ,
опущенного на директрису из точки
,
опущенного на директрису из точки![]() .
Из рисунка 12.15 очевидно, что
.
Из рисунка 12.15 очевидно, что![]() .
Тогда по определению параболы
.
Тогда по определению параболы![]() ,
то есть
,
то есть
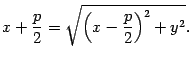
Возведем обе части последнего уравнения в квадрат:
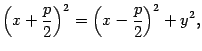
откуда
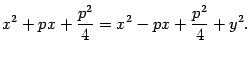
После приведения подобных членов получим уравнение (*).
Уравнение (*) называется каноническим уравнением параболы.
Парабола
обладает осью симметрии. Если парабола
задана каноническим уравнением, то ось
симметрии совпадает с осью
![]() .
.
Доказательство. Проводится так же, как и предыдущее доказательство
Точка пересечения оси симметрии с параболой называется вершиной параболы.
Если
переобозначить переменные
![]() ,
,![]() ,
то уравнение (*) можно записать в виде
,
то уравнение (*) можно записать в виде
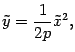
который совпадает с обычным уравнением параболы в школьном курсе математики. Поэтому параболу нарисуем без дополнительных исследований
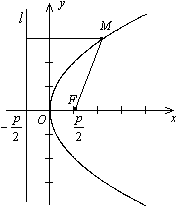
Уравнение
директрисы![]() :
:![]() ,
фокус —
,
фокус —![]() ,
таким образом начало координат
,
таким образом начало координат![]() —
середина отрезка
—
середина отрезка![]() .
По определению параболы для любой точки
.
По определению параболы для любой точки![]() ,
лежащей на ней выполняется равенство
,
лежащей на ней выполняется равенство![]() .
.![]() и
и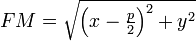 ,
тогда равенство приобретает вид:
,
тогда равенство приобретает вид:
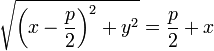 .
.
После
возведения в квадрат и некоторых
преобразований получается равносильное
уравнение
![]() .
.
Парабола — кривая второго порядка.
Она имеет ось симметрии, называемой осью параболы. Ось проходит через фокус и перпендикулярна директрисе.
Пучок лучей параллельных оси, отражаясь в параболе собирается в её фокусе. Для параболы
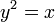 фокус
находится в точке (0,25; 0).
фокус
находится в точке (0,25; 0).Если фокус параболы отразить относительно касательной, то его образ будет лежать на директрисе.
Все параболы подобны. Расстояние между фокусом и директрисой определяет масштаб.
При вращении параболы вокруг оси симметрии получается эллиптический параболоид.
|
Вид кривой |
Каноническое уравнение |
Инварианты |
|
Невырожденные
кривые( | ||
|
Эллипс |
|
|
|
Гипербола |
|
|
|
Парабола |
|
|
|
Вырожденные кривые (Δ = 0) | ||
|
Точка |
|
|
|
Две пересекающиеся прямые |
|
|
|
Две параллельные прямые |
|
|
|
Одна прямая |
x2= 0 |
|
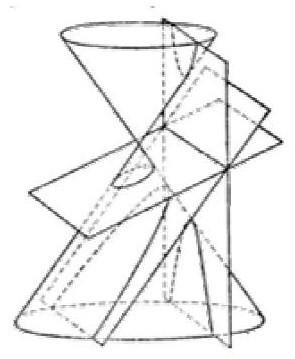
Конические сечения
Функции двух переменных
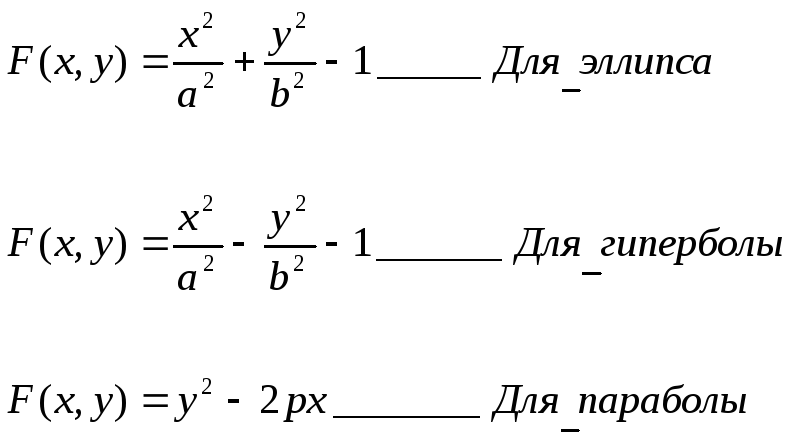
Преобразование координат
Параллельный перенос:
Пусть
на плоскости заданы две декартовы
прямоугольные системы координат:
![]() ("старая")
и
("старая")
и![]() ("новая"),
причем как оси абсцисс, так и оси ординат
обеих систем параллельны и одинаково
направлены
("новая"),
причем как оси абсцисс, так и оси ординат
обеих систем параллельны и одинаково
направлены
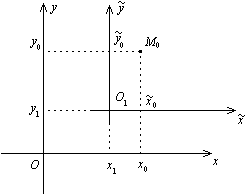
Параллельный перенос системы координат
В этом случае говорят, что одна система координат получается из другой "параллельным переносом".
Пусть
начало
![]() "новой"
системы координат имеет в "старой"
системе координат координаты
"новой"
системы координат имеет в "старой"
системе координат координаты![]() ,
и пусть
,
и пусть![]() --
некоторая точка плоскости. Обозначим
координаты точки
--
некоторая точка плоскости. Обозначим
координаты точки![]() в
"старой" системе координат
в
"старой" системе координат![]() ,
а в "новой" --
,
а в "новой" --![]() .
Из рис. 12.19 ясно, что
.
Из рис. 12.19 ясно, что![]() ,
,![]() .
Откуда
.
Откуда![]() ,
,![]() .
Так как точка
.
Так как точка![]() взята
произвольно, то индекс 0 в записи ее
координат, как "старых", так и
"новых", можно убрать. Получаем
связь между "старыми" и "новыми"
координатами точки при параллельном
переносе осей координат:
взята
произвольно, то индекс 0 в записи ее
координат, как "старых", так и
"новых", можно убрать. Получаем
связь между "старыми" и "новыми"
координатами точки при параллельном
переносе осей координат:
|
|
(1) |
Выясним теперь, как связаны друг с другом уравнения одной и той же кривой в "старых" и "новых" координатах.
Пусть
некоторая кривая задана уравнением
![]() .
Тогда в системе координат
.
Тогда в системе координат![]() ,
полученной параллельным переносом, с
началом в точке
,
полученной параллельным переносом, с
началом в точке![]() уравнение
кривой будет иметь вид
уравнение
кривой будет иметь вид![]() .
.
Однако, для практического использования это предложение удобнее сформулировать немного по-другому.
Пусть
некоторая кривая задана уравнением
![]() .
Тогда в системе координат
.
Тогда в системе координат![]() ,
полученной параллельным переносом, с
началом в точке
,
полученной параллельным переносом, с
началом в точке![]() уравнение
кривой будет иметь вид
уравнение
кривой будет иметь вид![]() .
.
Доказательство обоих предложений очевидным образом следует из формул (1) связи между старыми и новыми координатами.
Поворот:
Выведем формулу преобразования координат при повороте координатных осей.
Повернём оси координат на угол α относительно
исходной системы координат. Координаты точки М
в системе координат x′Oy′ равны x′ и y′. Найдём её
координаты в системе коорднат xOy. В треугольнике
CMD ∠CMD = α , OD=x′, MD=y′.
Следовательно, x=OA=OB-AB=OB-CD, y=MA=AC-CM=DB+CM.
Поскольку
OB = x′ cos α, CD = y′ sin α,
CM = y′ cos α, DB = x′ sin α,
x = x′ cos α − y′ sin α,
то
y = x′ sin α + y′ cos α.
Эти формулы выражают старые координаты (x,y) произвольной точки М через новые координаты (x′,y′) этой же точки при повороте осей на угол α.
Формулы, выражающие новые координаты (x′,y′) точки М через её старые координаты (x,y), получим из следующих соображений: если новая система получена поворотом старой на угол α, то старая система получается поворотом
новой на угол (-α), поэтому в равенствах можно поменять местами старые и новые координаты, заменяя одновременно α на (-α).
Выполнив это преобразование, получим
x′ = x cos α + y sin α,
y′ = − x sin α + y cos α.
При этом, например, уравнения директрис эллипса (гиперболы) и параболы принимают вид:
a
x′ cos α − y′ sin α = ± ;
e
p
x′ cos α − y′ sin α = − .
2
Классификация кривых второго порядка
Существуют следующие классы кривых второго порядка на евклидовой плоскости:
Эллиптического вида
А) Эллипс
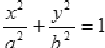
В) Мнимый эллипс
![]()
С) Эллипс вырожденный в точку
![]()
Кривые гиперболического типа
А) Гипербола
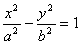
В) Пара вещественных пересекающихся прямых
![]()
Параболического типа
А) Парабола
![]()

В) Пара вещественных параллельных прямых
y 2 − a2 = 0
С) Пара мнимых параллельных прямых
y2 + a2 = 0
D) Пара совпадающих прямых
y 2 = 0
Основные моменты доказательства теорем:
Коэффициенты при произведении xy либо равны 0 либо нет.
В каждой группе выделяется полный квадрат если это возможно.
Тогда уравнение будет приведено либо к 1 либо к 2 типу.
Если это невозможно, тогда один из коэффициентов при квадрате равен 0. А другой обязательно не 0 и получаем уравнение 3 типа.
А
когда коэффициент
![]() не
0 переводим к предыдущему с помощью
поворота осей.
не
0 переводим к предыдущему с помощью
поворота осей.
Алгебраические поверхности 2 порядка в трехмерном Евклидовом пространстве
a11x2 + a22y2 + a33z2 + 2a12xy + 2a13xz + 2a23yz + 2a10x + 2a20y + 2a30z + a00 = 0, где коэффициенты a11, a22, a33, a12, a13, a23, a10, a20, a30, a00 − действительные числа, причем a11, a22, a33, a12, a13, a23 не равны нулю одновременно.
Особые поверхности 2 порядка:
Действительный эллипсоид
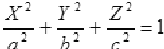
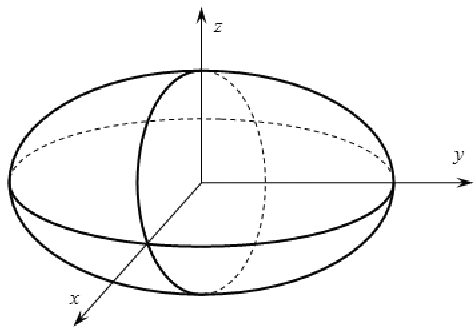
Мнимый эллипсоид
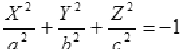
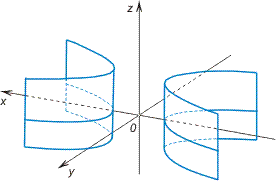
3)Однополостный гиперболоид
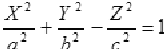

Двуполостный гиперболоид
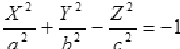
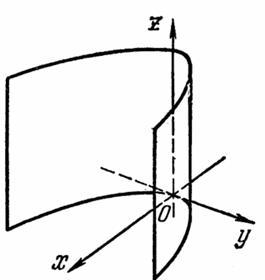
Эллиптический параболоид
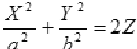
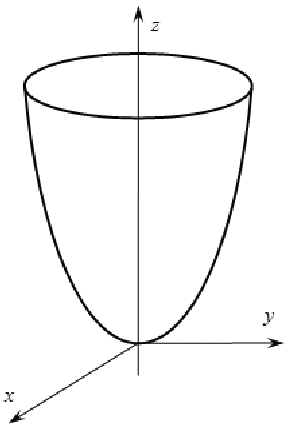
Гиперболический параболоид
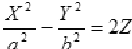
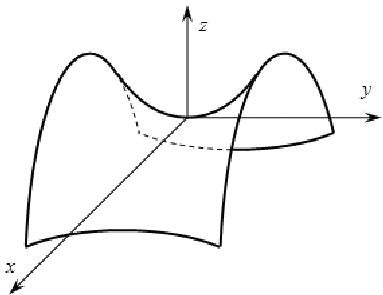
В) Не распадающиеся действительные поверхности
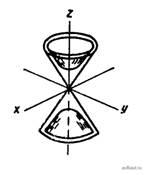
Действительный конус
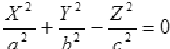
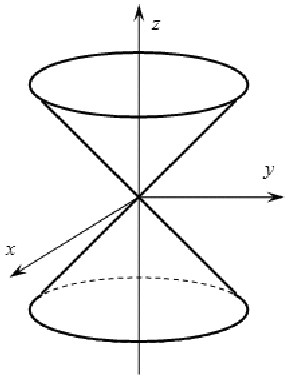
Мнимый конус
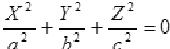
Эллиптический цилиндр
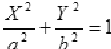
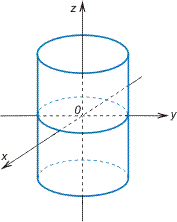
Мнимый эллиптический цилиндр
![]()
Гиперболический цилиндр
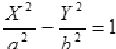
Параболический цилиндр
Y
2 =
2pX