Лабораторная работа №2. Создание пользовательских модулей

Цель работы – познакомиться с программным компонентом - модулем, изучить структуру модуля. Познакомиться с назначением интерфейсного блока и оператором EXTERNAL. Научиться создавать модули с интерфейсами процедур, научиться создавать универсальную модульную процедуру решения типовой задачи вычислительной математики.

Постановка задачи.

1. Создать модуль с интерфейсным блоком, содержащий интерфейсы процедур для задания из лабораторной работы №1. Выполнить эту задачу с использованием модуля.

2. Согласно индивидуальному заданию разработать модуль, содержащий подпрограмму, которая реализует численный метод решения одной из задач вычислительной математики, например нахождения интеграла для любой подинтегральной функции или решения уравнения любого вида. Подпрограмма, реализующая численный метод, должна получать имя функции, описывающей решаемое уравнение или подинтегральную функцию, как фактический параметр. Разработанную процедуру протестировать на двух различных функциях вида y=f(x), выбранных студентом самостоятельно.

Задание №2 выполнить тремя способами:

2.1.Решить задачу с использованием оператора EXTERNAL. Процедуру, реализующую метод, поместить во внешний файл.

2.2.Процедуру, реализующую заданный численный метод, оформить как модульную процедуру, поместив ее в модуль. Разработать модуль общих описаний.

2.3.Создать модуль с интерфейсным блоком для двух исследуемых функций, модуль с интерфейсом процедуры, реализующей численный метод. Использовать внешнюю процедуру из пункта 2.1.

Описание численных методов. Методы численного интегрирования.

Эти методы применяются для приближенного вычисления определенного интеграла вида: . Функцияf(x) задана на отрезке [a, b]. Этот отрезок разбивается на n равных частей длины h=(b-a)/n.

Определенный интеграл представляет собой площадь, ограниченную кривой f(x), осью x и прямыми x=a и x=b. Приблизительно эта площадь представляется суммой площадей полос, основания которых одинаковы и равны h, а высоты равны значениям функции в точках разбиения. Обозначим точки разбиения x₀=a, x₁=a+h, x₂= a+2h,… x_n=b, а значения функции в этих точках соответственно y_o=f(x₀); y₁=f(x₁), y₂=f(x₂), ... y_n=f(x_n).

1. Метод прямоугольников.

,

2. Метод трапеций.

3. Метод Симпсона (парабол).

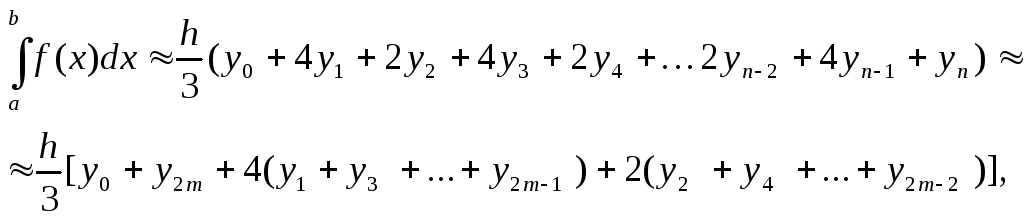
где n=2*m число разбиений отрезка [a, b], кратное двум.

4. Метод Ньютона.

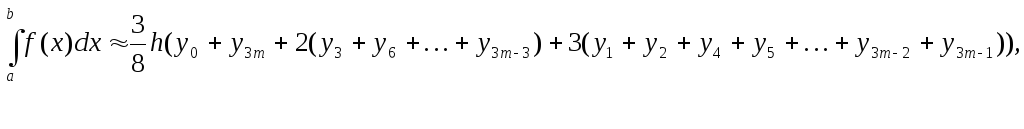где n=m*3– число разбиений отрезка [a, b], кратное трем.

Решение алгебраических и трансцендентных уравнений.

При решении уравнений вида f(x)=0 точно вычислить корни уравнения возможно лишь в частных случаях. Поэтому для нахождения корней уравнения могут использоваться приближенные методы. При изложении этих методов предполагается, что известен отрезок, а≤ x ≤b, внутри которого существует корень, и задача вычисления корня решается с заданной точностью.

1. Метод итераций

Сущность метода итераций заключается в следующем. Для данного метода исходное уравнение должно быть представлено в видеи выбрано начальное приближениеx₀на заданном отрезке. При нахождении корня уравнения этим методом должно выполняться условие . Новое значение корня вычисляется через предыдущее по формуле. Итерационный процесс уточнения корня заканчивается при достижении условия, где ε – допустимая погрешность.

2. Метод Ньютона

В соответствии с этим методом каждое следующее приближение к корню ищется по формуле:

Итерационный процесс уточнения корня заканчивается при достижении условия: , где ε – заданная точность.

3. Метод половинного деления.

Отрезок [a, b] делится пополам , и определяется значение функцииf(x) на концах отрезков [а, х] и [х, b]. Корень находится в той половине отрезка [a, b], на концах которой f(x) имеет разные знаки. Если f(a) и f(x) имеют разные знаки, то далее в качестве отрезка, содержащего корень, рассматриваем [a, х], иначе - [х, b]. Новый отрезок делится пополам, и такой процесс повторяется до тех пор, пока отрезок не станет меньше заданной точности ε.

4. Метод секущих

При использовании этого метода каждое следующее приближение вычисляется по формуле:

Процесс уточнения корня заканчивается при выполнении условия , где ε – заданная точность.