14.5 Інтегральний метод встановлення порядку реакцій

Розв’язання зворотних задач кінетики розглянемо на прикладі встановлення формального порядку реакцій і розрахунків констант швидкості. На практиці задача ставиться таким чином: за наявними даними із залежності ступеню перетворення або концентрації від часу визначити порядок реакції і константи швидкості. Коли концентрації усіх реагентів одинакові, це зводиться до оцінки параметрів k та n диференціального рівняння (14.35):

. (14.35)

У прикладі 14.3 було розглянуто лдержання порядку реакції на основі диференуціювання кінетичних кривих з подальшим знаходженням степеневого рівняння швидкості (у логарифмічній формі). Такий метод носить назву диференціального методу або методу Вант-Гоффа). Його недоліком є необхідність проведення чисельного диференціювання експериментальних даних. Ця процедура, як відомо, може мати значну й непередбачену обчислювальну погрішність.

З використанням комп’ютерів цю задачу доцільно розв’язувати інтегральним методом, що не вимагає процедури диференціювання. Проінтегруємо рівняння (14.35) дляn1 при початкової умові: С(0) = С₀:

. (14.36)

Дляn = 1 інтегрування (14.35) приводить до рівняння:

. (14.37)

Для подальшого рішення можна виразити С через відомі величини С₀іtі невідомі параметриnіkі знайти оцінку параметрів методом найменших квадратів за критерієм суми квадратів відхилень між експериментальними і розрахованими значеннямиk. Але при цьому виникає проблема, що для різних ділянок необхідно використовувати два рівняння (одне – з (14.36), інше – з (14.37)).

Задачу можна спростити, якщо обирати значення n і розраховувати для цих величин серію констант швидкості у кожній зm експериментальних точок за рівняннями (14.36) і (14.37) і для кожного з наборів розраховувати середнє значення константи:

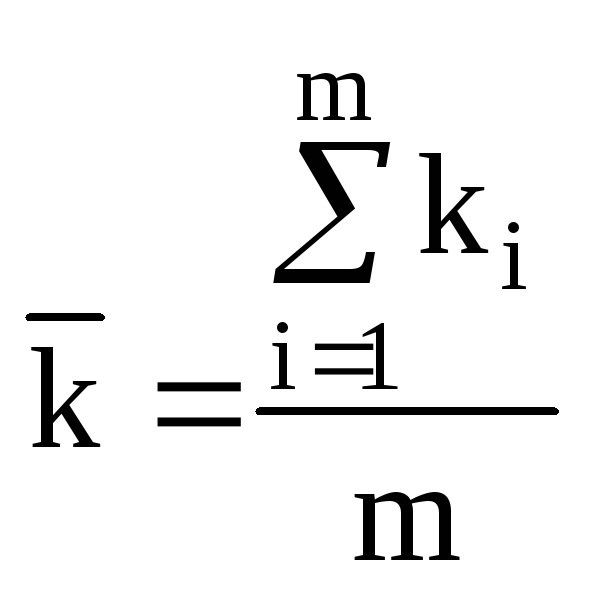. (14.38)

Виходячи з цього, можна сформулювати оптимізаційну задачу: знайти таке значення n, при яких функціонал (14.39) буде приймати мінімальне значення.

. (14.39)

Такий вид функціоналу обумовлений тим, що для різних порядків константи швидкості мають різні розмірності, і якщо обирати за функціонал просту суму квадратів різниць констант і середньої константи, то одержані величини для різних nне можна порівняти одне з іншим. Ділення на середнє значення приводить до безрозмірного функціоналу. Це дає можливість обирати оптимальну величинуn.

На практиці формальний порядок може мінятися в максимальних межах від -4 до 4 (із запасом), достатня точність визначення порідку: 0,05. Це надає можливості розраховувати функціонал при 0,99 < n < 1,01 за рівнянням (14.36), а у противному випадку – за рівнянням (14.37), користуючись стратегією одного з методів одновимірної оптимізації, наприклад параболічного пошуку.

При використанні Excelдля виконання розрахунків можна використовувати надбудову «Поиск решения», але в рамках цій програми неможливо проводити розрахунки за двома рівняннями. На практиці можна на першому етапі перевірити наявність першого порядку. Для цього приводимо рівняння (14.37) до виду:

lnC=lnC₀–kt. (14.40)

З (14.40) випливає, що в разі наявності першого порядку повинна спостерігатися лінійна залежність між логарифмом концентрації і часом. Якщо експериментальні точки добре групуються навколо прямої – можна вважати, що реакція підпорядковується першому порядку і подальші розрахунки не мають сенсу. У противному випадку треба проводити розрахунок порядку.

Розглянутий метод можна використовувати, як «скорочений» метод розрахунку порядку і константи швидкості. Але слабким місцем методу є те, що відбвауться порівняння між собою величин, що одержані шляхом розрахунків. Більш природнім є розробка такого методу, у якому розрахункова величина порівнюється з такою, що визначається в експерименті, наприклад з концентрацією. У цьому випадку можна використати наступний варіант інтегрального методу. З рівняння (14.36) виразимо концентрацію:

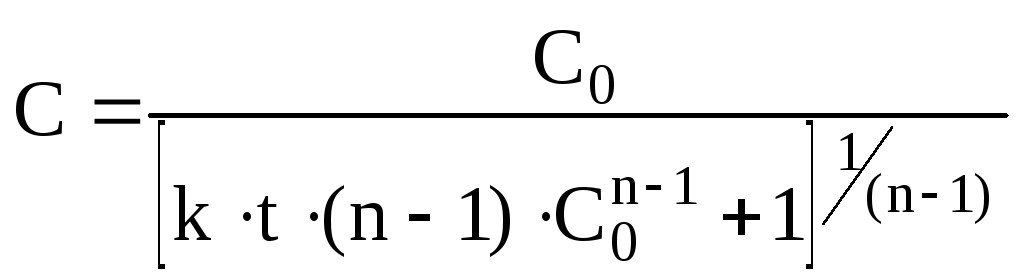(14.41)

Тоді для розрахунків порядку реакції та константи швидкості можна використати метод найменших квадратів і побудувати наступний функціонал для мінімізації:

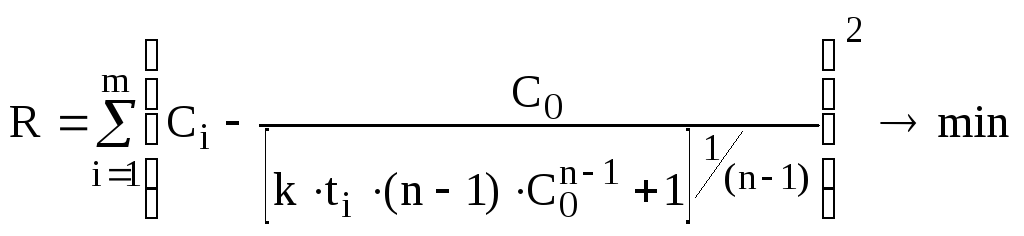. (14.42)

При этом, в качестве начального приближения можно использовать значения порядка и константы скорости, полученные по алгоритму (14.39)

Приклад 14.4

Розрахувати порядок реакції взаємодії лауринової кислоти і лаурилового спирту користуючись даними залежності ступеню перетворення від часу (табл. 14.2).

Розв’язання

На першому етапі перевіряємо, чі можна описати експериментальну залежність кінетичним рівнянням 1-го порядку. Дл цього за експериментальними даними будуємо залежність логарифма залишкової концентрації реагенту від часу.

Таблиця 14.2 - Залежність від часу ступеню перетворення (р, %) в реакції 0,2 кмоль/м лауринової кислоти з 0,2 кмоль/м³лаурилового спирту у середовищі лауриллаурату при 195^оС

t ,хв	p,%	t,хв	p,%	t,хв	p,%
0	0	300	49,7	780	66,9
15	6,2	360	53,6	900	69,2
30	8,5	420	57	1080	71,6
60	18,5	480	59,7	1320	74,1
120	33,1	555	61,6	1620	76,6
180	40,7	600	62,9
240	44,7	660	64,6

Оскільки задано ступінь перетворення у %, шукану концентрацію розраховуємо за формулою:

(14.43

З рис. 14.5 випливає, що залежність логарифму концентрації від часу не є лінійною. Це вказує, що порядок реакції, шо вивчена, відрізняється від першого.

На другому етапи будемо розвязувати основну задачу.

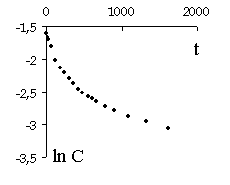
Рисунок 14.5 – Залежність логарифма концентрації лаурілового спирту й лаурілової кислоти від часу

На другому етапі укладаємо скрипт Scilab для розвязання задачі (14.39) (листінг 14.4.1)

Листінг 14.4.1

//Вхідні дані

t=[15 30 60 120 180 240 300 360 420 480 555 600 660 780 900 1080 1320 1620];

p=[6.2 8.5 18.5 33.1 40.7 44.7 49.7 53.6 57 59.7 61.6 62.9 64.6 66.9 69.2 71.6 74.1 76.6];

//Перерахунок у концентрації

C0=0.2;

x=C0*(100-p)/100;

m=size(t,2)

n0=2//Початкове наближення

function k=rate_k(n)// розрахунок констант швидкості

k=(1/x(i)^(n-1)-1/C0^(n-1))/(n-1)/t(i)

endfunction

function f=kser(n)// розрахунок функціоналу

kk=zeros(m,1)

for i=1:m

kk(i)=rate_k(n)

end

kz=mean(kk)

f=0

for i=1:m

f=f+((kk(i)-kz)/kz)^2

end

endfunction

function [f,g,ind]=cost(n,ind)//функція цілі для оптимізації

f=kser(n)

g=numdiff(kser,n)

endfunction

//begin

[fmin, nmin]=optim(cost,n0)//nmin – шуканий порядок

k=zeros(m,1);//масив констант

for i=1:m

k(i)=rate_k(nmin);

end

ks=mean(k)// середнє значення

dk=st_deviation(k)//стандартне відхилення

[t',k]//друк результатів

Результати розрахунків наведені у протоколі 14.4.1

Протокол 14.4.1

nmin =

2.7509262

fmin =

0.1115690

ks =

0.0731172

dk =

0.0059233

ans =

15. 0.0756018

30. 0.0536415

60. 0.0686478

120. 0.0813989

180. 0.0795126

240. 0.0725735

300. 0.0742913

360. 0.0753378

420. 0.0770242

480. 0.0778956

555. 0.0748340

600. 0.0745147

660. 0.0747790

780. 0.0727029

900. 0.0729052

1080. 0.0713786

1320. 0.0698942

1620. 0.0691761

Як випливає з наведених даних, порядок реакції є близьким до 2,8, а константа швидкості 0 до 0,073.

Одержані результати використовуємо за початкове наближення до розвязання задачі (14.42) Для цього створили скрипт (листінг 14.4.2)

Листінг 14.4.2

t=[0 15 30 60 120 180 240 300 360 420 480 555 600 660 780 900 1080 1320 1620];

p=[0 6.2 8.5 18.5 33.1 40.7 44.7 49.7 53.6 57 59.7 61.6 62.9 64.6 66.9 69.2 71.6 74.1 76.6];

C0=0.2;

x=C0*(100-p)/100;

m=size(t,2)

z0=[2.8,0.073]

function y=fi(z)//одиничний розрахунок

n=z(1)

k=z(2)

y=C0/(k*t(i)*(n-1)*C0^(n-1)+1)^(1/(n-1))

endfunction

function f=sumkw(z)//сума квадратів

f=0

for i=1:m

f=f+(fi(z)-x(i))^2

end

endfunction

function [ff,gg,ind]=cost(z,ind)

ff=sumkw(z)

gg=numdiff(sumkw,z)

endfunction

[fmin,zmin]=optim(cost,z0)

for i=1:m

y(i)=fi(zmin);

end

В результате расчетов получили: n = 2,79 2,80,k= 0,081, сума квадратів відхилень: 0.0000681.

Подібним чином можна розраховувати порядок реакції і набор констан швидкості, наприклад, в разі розрахунків енергії активації і логарифму передекспоненти. Наприклад, якщо наявні експериментальні дані з rсерій експериментів поm(і) експериментів у кожній серії (і = 1,2,…,r), те функціонал для мінімізації буде мати вигляд:

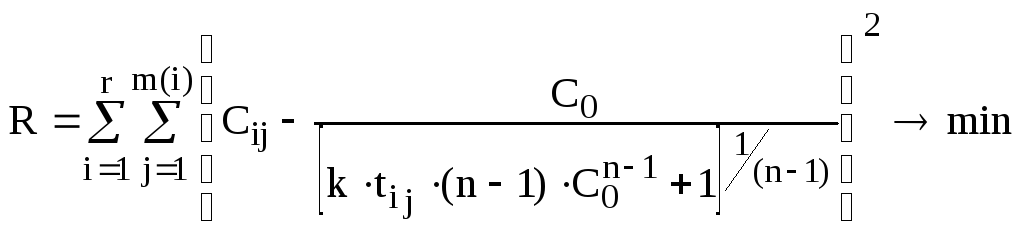(14.44)

Це дозволяє розрахувати набір констант того ж самого порядку при різних температурах і далі, користуючись МНК, розрахувати енергію активації, як це описано у прикладі (14.3)