
21-25 емтихан сурактары
.docx21. Quadratic forms. Reducing a quadratic form to a canonical type.
A
QF of real variables x1,x1,…,xn
is a polynomial of the 2nd
degree according to these variables which doesn’t contain a free
term and terms of the 1st
degree. If n=2, then f(x1,x2)=a11x2+2a12x1x2+a22x2.
A matrix
 at which
at which
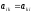 is called matrix
of quadratic form
is called matrix
of quadratic form
 and the corresponding determinant – determinant
of this quadratic
form.
Since A
is a symmetric matrix then the roots
and the corresponding determinant – determinant
of this quadratic
form.
Since A
is a symmetric matrix then the roots
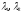 and
and
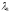 of the characteristic equation are real numbers.
of the characteristic equation are real numbers.
Let
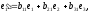
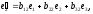
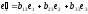 be
normalized eigenvectors corresponding to characteristic numbers
be
normalized eigenvectors corresponding to characteristic numbers
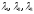 in an orthonormal basis
in an orthonormal basis
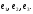 The vectors
The vectors
 form an orthonormal basis.
form an orthonormal basis.
The
matrix
 is the transition matrix from the basis
is the transition matrix from the basis
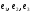 to
the basis
to
the basis
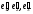
Formulas of transformation of coordinates at transition to the new orthonormal basis have the following form:
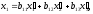

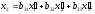
Transforming
by these formulas the quadratic form
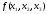 we
obtain the following quadratic form:
we
obtain the following quadratic form:

It
does not contain terms with
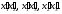
We
say that a quadratic form
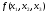 has
been reduced to the canonical
type
by an orthogonal transformation B.
has
been reduced to the canonical
type
by an orthogonal transformation B.
22. Definite quadratic forms. Criterion of Sylvester.
A
quadratic form
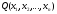 is called positive
definite
(negative
definite)
if for all values
is called positive
definite
(negative
definite)
if for all values
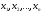 the condition
the condition
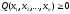 (
(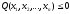 )
holds and
)
holds and
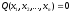 only for
only for
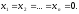
For
example,
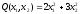 is positive definite;
is positive definite;
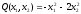 is negative definite. Positive definite and negative definite
quadratic forms are called definite.
is negative definite. Positive definite and negative definite
quadratic forms are called definite.
A
quadratic form
 is called quasi-definite
(either non-negative
or
non-positive)
if it takes either only non-negative values or non-positive values,
but it takes 0 not only for
is called quasi-definite
(either non-negative
or
non-positive)
if it takes either only non-negative values or non-positive values,
but it takes 0 not only for
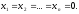
The determinants

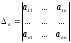 are
called angular
minors of
a matrix
are
called angular
minors of
a matrix

1. A quadratic form is positive definite if and only if all the angular minors of its matrix are positive.
2.
A quadratic form is negative definite if and only if the signs of
angular minors alternate as follows:
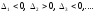
23. Reducing an equation of curve of the second order to a canonical type.
Let
an equation of a curve of the second order in rectangular system of
coordinates
 be given:
be given:
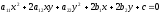 Consider
the quadratic form connected with the equation (1):
Consider
the quadratic form connected with the equation (1):
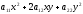 .Reduce
the quadratic form to canonic type
.Reduce
the quadratic form to canonic type
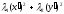 by an orthogonal transformation of variables:
by an orthogonal transformation of variables:
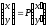
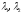 are eigen-values of the matrix
are eigen-values of the matrix
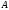 ,
and the columns of the matrix
,
and the columns of the matrix
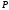 are orthogonal normalized eigen-vectors (columns) of the matrix
are orthogonal normalized eigen-vectors (columns) of the matrix
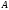 .
The matrix
.
The matrix
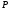 by properties of orthogonal matrices has the following type:
by properties of orthogonal matrices has the following type:
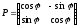 Using
the formulas (2), express the linear terms
Using
the formulas (2), express the linear terms
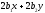 of the equation (1) by the coordinates
of the equation (1) by the coordinates
 .
In result in the system
.
In result in the system
 the equation of the curve takes the following type:
the equation of the curve takes the following type:
 .
Further, extracting complete squares on both variables by parallel
transfer of axes of coordinates of the system
.
Further, extracting complete squares on both variables by parallel
transfer of axes of coordinates of the system
 pass to the system
pass to the system
 in which the equation of the curve has canonic type. An equation of a
surface of the second order can be reduced to canonic type by analogy
in which the equation of the curve has canonic type. An equation of a
surface of the second order can be reduced to canonic type by analogy
24. Unitary space. Gram matrix, Hermitian matrix, unitary matrix.
A complex linear space where the following conditions hold:
1)
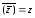 ;
;
2)
A complex number z is real iff
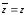 ;
;
3)
The number
 is always real and nonnegative;
is always real and nonnegative;
4)
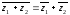 ,
,
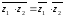 .
.
is called unitary iff every ordered pair of elements x and y is put in correspondence a complex number (x,y) called their scalar product so that the following conditions hold:
(1)
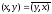 ;
;
(2)
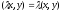 for every complex number
for every complex number
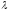 ;
;
(3)
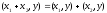 ;
;
(4)
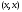 is a real nonnegative number, and
is a real nonnegative number, and
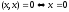 .
.
Let
in
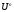 a basis
a basis
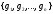 be given. The scalar product of elements
be given. The scalar product of elements
 and
and
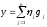 is presented as
is presented as
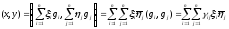 ,
where
,
where
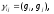
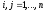 are components of the matrix
are components of the matrix
 named the basis
matrix of Gram.
named the basis
matrix of Gram.
A
matrix
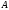 satisfying the property
satisfying the property
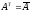 is called Hermitian.
A matrix
is called Hermitian.
A matrix
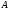 satisfying the properties
satisfying the properties
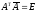 and
and
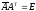 is called unitary.
is called unitary.
25. Linear operators in a unitary space.
A
linear operator
 acting in a unitary space
acting in a unitary space
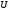 is called Hermitian
conjugate
to a linear operator
is called Hermitian
conjugate
to a linear operator
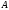 if for all
if for all
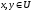 the following holds:
the following holds:
 .
.
Theorem
1.
For linear operators
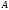 and
and
 acting in a unitary space
acting in a unitary space
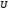 the following holds:
the following holds:
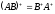 and
and
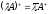
Proof:
Prove the first assertion. We have
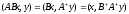 for all
for all
 ,
and consequently
,
and consequently
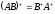 .
.
Similarly,
 for all
for all
 and every complex number
and every complex number
 .
.
Theorem
2.
The matrix of an operator
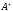 that is Hermitian conjugate to an operator
that is Hermitian conjugate to an operator
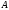 in
in
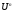 in a basis
in a basis
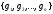 is
defined by the following equality:
is
defined by the following equality:
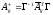 .
.
A
linear operator
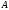 acting in a unitary space
acting in a unitary space
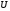 is called Hermitian
self-conjugate
(or just Hermitian)
if
is called Hermitian
self-conjugate
(or just Hermitian)
if
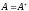 .
.
Properties of Hermitian operators:
1. Eigen-values of a Hermitian operator are real numbers.
2. Eigen-vectors corresponding to distinct eigen-values of a Hermitian operator are orthogonal.
3. For every Hermitian operator there exists an orthonormal basis consisting of its eigen-vectors.
4.
In an orthonormal basis of a unitary space
 a Hermitian operator has a Hermitian matrix.
a Hermitian operator has a Hermitian matrix.
An
eigen-value
 of a linear operator
of a linear operator
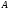 is called degenerate
if an invariant eigen-subspace corresponding to it has the dimension
greater than 1.
is called degenerate
if an invariant eigen-subspace corresponding to it has the dimension
greater than 1.
A
linear operator
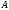 acting in a unitary space
acting in a unitary space
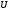 is called unitary
(or isometric)
if for all
is called unitary
(or isometric)
if for all
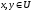 the following holds:
the following holds:
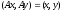 .
.
Properties of unitary operators:
1.
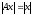 .
.
2.
If
 is a unitary operator then there exists the inverse operator
is a unitary operator then there exists the inverse operator
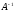 that is also unitary and
that is also unitary and
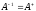 .
.
3.
A unitary operator transfers an orthonormal basis in an orthonormal
basis, and conversely if a linear operator
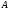 transfers an orthonormal basis to an orthonormal basis then
transfers an orthonormal basis to an orthonormal basis then
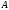 is unitary.
is unitary.
4.
If
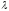 is an eigen-value of a unitary operator then
is an eigen-value of a unitary operator then
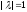 .
.
