
21 Контравариантные и ковариантные компоненты
.docx§21 Контравариантные и ковариантные компоненты. Инфинитезимальные афинные преобразования репера.
Умножим вектор
 (1)
(1)
скалярно
на вектор
 .
обозначая произведение
.
обозначая произведение
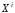 ,
получим с помощью формулы (1)
§20
,
получим с помощью формулы (1)
§20
 (2)
(2)
Компоненты
 носят название контравариантных
компонентов вектора, а компоненты
носят название контравариантных
компонентов вектора, а компоненты
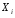 − ковариантных компонентов.
− ковариантных компонентов.
Умножая
обе части равенства (2) на
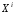 и суммируя по индексу
и суммируя по индексу
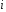 ,
получим
,
получим
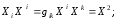 (3)
(3)
аналогично,
 (4)
(4)
Чтобы
перейти от ковариантных компонентов
вектора к контравариантным, надо
разрешить систему (2) из
 уравнений
уравнений
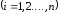 с
с
 неизвестными
неизвестными
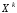
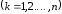 .
По известной формуле это решение будет
.
По известной формуле это решение будет
 (5)
(5)
где
 − приведенный минор элемента
− приведенный минор элемента
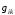 в определителе
в определителе
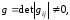
т.е.
адъюнкт элемента
 ,
деленный на определитель
,
деленный на определитель
 .
Все это относится также к инфинитезимальным
компонентам
.
Все это относится также к инфинитезимальным
компонентам
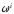 или
или
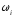 .
.
Для ортонормированного репера
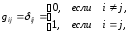
поэтому по формуле (2)
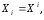
т.е.
ковариантные компоненты вектора равны
контравариантным. Мы будем писать без
различия
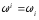 ,
,
 ,
сохраняя условие суммирования (2)
§19 по двум одинаковым, одному верхнему,
другому нижнему, индексам.
,
сохраняя условие суммирования (2)
§19 по двум одинаковым, одному верхнему,
другому нижнему, индексам.
Заметим,
что при косоугольном репере мы уже не
можем говорить, что уравнение (5) определяют
движения репера, так как наши трехгранники
теперь не конгруэнтны. Однако
преобразование координат
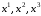 при переходе от одного координатного
трехгранника к другому будет определяться
линейной подстановкой. Действительно,
если обозначить через
при переходе от одного координатного
трехгранника к другому будет определяться
линейной подстановкой. Действительно,
если обозначить через
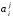 косинусы углов между старыми и новыми
осями, через
косинусы углов между старыми и новыми
осями, через
 − старые координаты произвольной точки,
через
− старые координаты произвольной точки,
через
 − новые координаты ее и через
− новые координаты ее и через
 координаты нового начала в старой
системе, то получим для старых координат
формулу
координаты нового начала в старой
системе, то получим для старых координат
формулу

Поскольку общая линейная подстановка определяет аффинное преобразование, уравнения (5) определяют инфинитезимальные афинные преобразования репера.
§ 22. Теория пфаффовых форм.
Видно,
что при заданном движении репера т.е.
при заданных координатах радиуса вектора
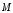 и единичных векторов осей
и единичных векторов осей
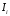 в виде функций от параметра
в виде функций от параметра
 ,
можем найти 6 компонент
,
можем найти 6 компонент
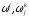 инфинитезимальных смещений репера.
инфинитезимальных смещений репера.
Возникает
вопрос: могут ли произвольно заданные
шесть форм
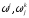 ,
линейные относительно
,
линейные относительно
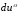 ,
представлять смещения трехгранника в
обычном пространстве?
,
представлять смещения трехгранника в
обычном пространстве?
Чтобы ответить на этот вопрос, придется сделать отступление в область анализа и рассмотреть свойства пфаффовых форм.
Пусть дана форма Пфаффа

Дифференциалы
независимых переменных
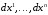 обыкновенно рассматриваются как новые
независимые переменные, но можно также
рассматривать их как заданные функции
независимых переменных
обыкновенно рассматриваются как новые
независимые переменные, но можно также
рассматривать их как заданные функции
независимых переменных

(направленное
смещение с определенным символом
дифференцирования). Рассмотрим два
символа дифференцирования
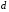 и
и
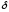 и два ряда различных дифференциалов
и два ряда различных дифференциалов
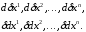
Пусть эти два символа дифференцирования переместительны
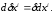 (1)
(1)
Теорема.
Если
символы дифференцирования
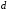 и
и
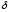 переместительны для независимых
переменных, то они переместительны и
для функции.
переместительны для независимых
переменных, то они переместительны и
для функции.
Действительно, рассмотрим функцию
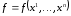
Тогда
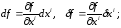
второе дифференцирование дает
 (2)
(2)
Здесь вторые члены равны в силу условия(1); в первых членах во второй формуле (2) индексы суммирования i на k и k на i,получим сумму
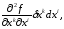
которая
отличается от аналогичной суммы в
выражении
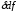 только порядком дифференцирования во
второй производной, а поскольку в
смешанных частных производных результат
дифференцирования не зависит от порядка
дифференцирования, первые члены в правых
частях выражений (2) совпадают, и имеем
только порядком дифференцирования во
второй производной, а поскольку в
смешанных частных производных результат
дифференцирования не зависит от порядка
дифференцирования, первые члены в правых
частях выражений (2) совпадают, и имеем
 (3)
(3)
