жогары ретти диф тендеулер

Қазақстан Республикасы Алматы облысы

Әл-Фараби атындағы Қазақ Ұлттық Университеті

Механика-математика факультеті

СӨЖ

Тақырыбы：Жоғарғы ретті дифференциалдық теңдеулер

Орындаған:Тілеміс Б.

Тексерген: Алдибеков Т. М.

Тобы: ИС-5А

Алматы 2013

Анықтама.

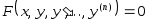
түріндегі теңдеу n–ретті дифференциалдық теңдеу деп аталады.

Егер (17)-ден n–і туынды табылатын болса, онда

теңдеуі ең жоғарғы туындысы арқылы шешілген n–ретті дифферен-циалдық теңдеу деп аталады.

Коши есебі:

бастапқы шарттарды қанағаттандыратын дифференциалдық теңдеудің шешімін табалық.

Теорема (Коши есебі шешімінің бар және оның жалғыз болуы туралы). функциясы

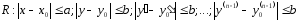
облысында мына екі шартты қанағаттандырсын делік:

1) 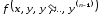функциясы өздерінің аргументтері бойынша үзіліссіз және шенелген:

;

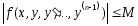2) функция үшін 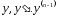айнымалылары бойынша

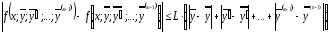
Липшиц шарты орындалады (Липшиц шарты функциядан айнымалылары бойынша алынған үзіліссіз дербес туындылары бар болғанда ғана орындалады), онда анықталған, өзінің n–і туындыларымен қоса үзіліссіз және бастапқы шарттарды қанағаттандыратын жалғыз шешімі бар болады.

Бұл теореманы жеңілдеу тұжырымдауға болады.

Егер дифференциалдық теңдеудің оң бөлігі үзіліссіз, шенелген және бойынша үзіліссіз дербес туындылары болса, онда Коши есебінің жалғыз шешімі бар болады.

Анықтамалар.

функциясы дифференциалдық теңдеудің жалпы шешімі деп аталады, егер ол:

1) -дың кез келген мәндерінде дифференциалдық теңдеуді қанағаттандырады;

2) берілген бастапқы шарттар бойынша функциясы бастапқы шарттарды қанағаттандыратын мынадай -і табуға болады.

Егер жалпы шешімінде -ң нақты мәндері алынатын болса, онда функция дифференциалдық теңдеудің дербес шешімі деп аталады.

түріндегі қатысы, мұндағы 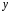айқын берілмеген, дифференциалдық теңдеудің жалпы интегралы деп аталады

теңдеуді интегралдау үшін бастапқы шарттарды қанағаттандыратын жалпы шешімін немесе дербес шешімін табу қажет.

Жоғарғы ретті дифференциалдық теңдеулерді интегралдаудың тәсілдері. I-класс. Тәуелсіз айнымалы және жоғарғы туындысы бар теңдеулер.

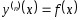
түріндегі теңдеуді қарастырамыз.

Екі бөлігін де 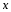бойынша интегралдаймыз:

тағы да интегралдаймыз:

.

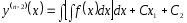Осы тәсілмен n рет интегралдаймыз, сонда

.

I-кластағы n-ретті ДТ тізбектей n рет интегралдау тәсілімен шешіледі.

Мысал. 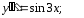теңдеуін шешелік.

;

;

.

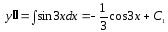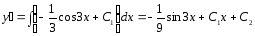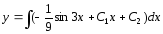
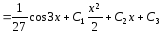II-класс. у функциясы және оның (k-1)-і ретіне дейінгі туындылары жоқ теңдеулер.

түріндегі ДТ қарастырамыз.

Жаңа айнымалы енгіземіз:

,

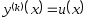сонда

.

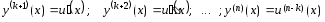u(х) функциясы мен оның алынған туындыларын қарастырылатын теңдеуге қоямыз:

.

Сонымен, 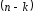- ретті теңдеу алынды, яғни ДТ-ң реті төмендетілді. Жаңа ДТ-ң шешімі

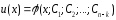
функциясы болсын делік. Мұны (20) теңдеуге қоямыз:

- k ретті дифференциалдық теңдеу аламыз, ал бұл k рет дифферен-циалдау арқылы шешіледі (1-класс).

Мысалдар. 1. 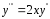үшінші ретті ДТ шешелік.

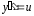ауыстыруын алайық, 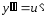. Бұларды теңдеуге қою арқылы 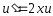бірінші ретті ДТ-і аламыз. Айнымалыларын ажыратамыз:

;

.

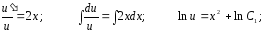
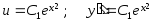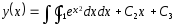Бұл теңдеу квадратурада шешіледі.

2. ;

; ; ; ;

;;;

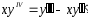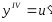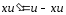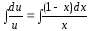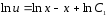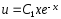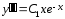
бұл теңдеуді бөліктеп үш рет интегралдау арқылы шешу керек (1-класс)

III-класс. Тәуелсіз айнымалы х-і жоқ теңдеулер.

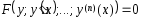
түріндегі теңдеуін қарастырамыз.

Тәуелсіз жаңа айнымалы үшін у-ті аламыз және ауыстыру орындаймыз:

.

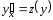Екінші, үшінші және т.б. туындыларын алу үшін осы жаңа функциядан күрделі функция есебінде туынды табамыз:

;

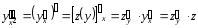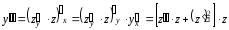
және т.б.

Табылған туындыларды теңдеуге қойып, реті бірге кеміген ДТ аламыз:

.

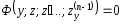Шешімі мына түрде табылды делік:

Енді ауыстыруға қайта оралып айнымалылары ажыратылған бірінші ретті ДТ аламыз:

.

Мысал. 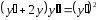ДТ шешелік. Мұнда тәуелсіз айнымалы х жоқ. 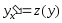ауыстыруын орындаймыз. ; 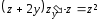- бұл біртекті теңдеу. - ауыстыруын аламыз, . Теңдеуге қоямыз: 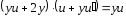.у-і қысқартамыз: .

;

; ;

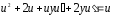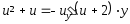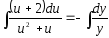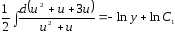- біртекті теңдеудің шешімі

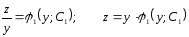немесе ,

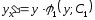ал бұл айнымалысы ажыратылған ДТ.

IV класс. Сол бөлігі толық туынды болып келген теңдеулер.

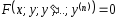
теңдеуін қарастырамыз және

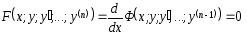
болсын делік. Жаңа дифференциалдық теңдеудің екі бөлігін де интегралдаймыз, сонда .

ДТ реті бірге төмендеді.

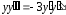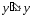Мысалдар. 1..Бұл III-кластың теңдеуі. IV-кластың тәсілімен шешіп көрелік. , екі бөлігін де -ке бөлеміз: енді интегралдаймыз: ;

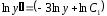- теңдеудің х-і жоқ.

; ; ; ;

; ; ;

;

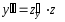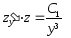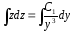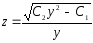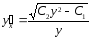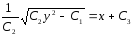
• бұл үшінші ретті ДТ жалпы интегралы, сондықтан оның үш еркін тұрақтысы бар.

2. ;

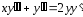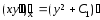; ; - бұл ДТ реті бірге төмендеді.

3. .

; ; ;

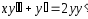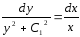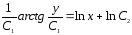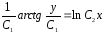; - бұл ДТ жалпы интегралы.