
11-15матан
.docx11) Бірінші текті қисық сызықты интегралды есептеу.
1. Қисық теңдеуі айқын түрде берілген жағдай.
2. Қисық теңдеуі параметрлік түрде берілген жағдай.
Айталық,
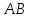 жазықтығы белгілі бір жатық немесе
құрама-жатық қисық,ал
жазықтығы белгілі бір жатық немесе
құрама-жатық қисық,ал
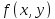 осы қисықта берілген функция болсын.
Осы қисық
осы қисықта берілген функция болсын.
Осы қисық
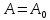 ,
,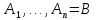 нүктелері арқылы
нүктелері арқылы
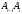 бөліктерге бөліктеуін қарастырып, әрбір
бөліктерге бөліктеуін қарастырып, әрбір
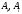 доғасынан кез келген бір
доғасынан кез келген бір
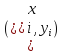 нүктесін алып,
нүктесін алып,
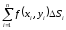 (1) қосындысын
түзейік, мұнда
(1) қосындысын
түзейік, мұнда
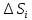 арқылы
арқылы
 доғасының
ұзындығы белгіленген. Егер
доғасының
ұзындығы белгіленген. Егер
 нөлге ұмтылғанда
нөлге ұмтылғанда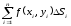 интегралдың белгілі бір
интегралдың белгілі бір
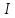 ақырлы шекке ұмтылса,онда бұл шек
ақырлы шекке ұмтылса,онда бұл шек
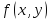 функциясының
функциясының
 қисығы бойынша бірінші
текті қисық сызықты интегралы
деп аталады және
қисығы бойынша бірінші
текті қисық сызықты интегралы
деп аталады және
 (2)
арқылы белгіленеді. Ескерту.
Мұнда
(2)
арқылы белгіленеді. Ескерту.
Мұнда
 және
және
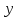 айнымалылары тәуелсіз айнымалылары
емес,
айнымалылары тәуелсіз айнымалылары
емес,
 қисығының бойында жату шартымен
байланысқан нүктелер. Бірінші текті
қисықсызықты интеграл ұғымының бір
айнымалының функциясының анықталған
интегралынан өзгешелігі жоқ дерлік
және ерлік оған оңай келтіріледі. Шынында
да,
қисығының бойында жату шартымен
байланысқан нүктелер. Бірінші текті
қисықсызықты интеграл ұғымының бір
айнымалының функциясының анықталған
интегралынан өзгешелігі жоқ дерлік
және ерлік оған оңай келтіріледі. Шынында
да,
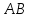 қисығынан параметр үшін бастапқы
қисығынан параметр үшін бастапқы
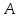 нүктесінен есептелетін
нүктесінен есептелетін
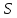 доға ұзындығын алып, бұл қисықты
доға ұзындығын алып, бұл қисықты
 (3)
(3)
теңдеулері
арқылы жазсақ,
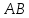 қисығында берілген
қисығында берілген
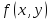 функциясы
функциясы
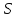 айнымалысының
айнымалысының
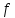 (
( ,
,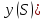 функциясына көшеді. Сонда
функциясына көшеді. Сонда
 нүктесіне сәйкес
нүктесіне сәйкес
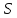 параметрінің мәнін
параметрінің мәнін
 арқылы белгілеп, (1) интегралдық қосындыны
арқылы белгілеп, (1) интегралдық қосындыны
 (4) түрінде жазсақ, ол
(4) түрінде жазсақ, ол
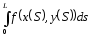 анықталған интегралына сәйкес интегралдық
қосынды.Ал (1) және (4) тең болғандықтан
оларға сәйкес интегралдар да тең, яғни
анықталған интегралына сәйкес интегралдық
қосынды.Ал (1) және (4) тең болғандықтан
оларға сәйкес интегралдар да тең, яғни
 (5)
(5)
Бұл
екі интегралдың бар болуы да, бар болмауы
да бірдей. Сондықтан
 функциясы
функциясы
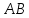 қисығы бойында үзіліссіз болса, онда
(2) қисықсызықты интеграл бар.
қисығы бойында үзіліссіз болса, онда
(2) қисықсызықты интеграл бар.
егерABқисығы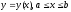 теңдеуіарқылыберілсе,
онда (9) формула
теңдеуіарқылыберілсе,
онда (9) формула
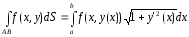 (10)
(10)
түріндежазылады.
Қисық теңдеуі параметрлік түрде берілген жағдай
Егер
AB
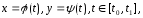 теңдеулері
арқылы берілген жатық қисық, ал
теңдеулері
арқылы берілген жатық қисық, ал
 осы қисықта берілген функция болса,
онда
осы қисықта берілген функция болса,
онда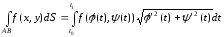 (1)
теңдігі орындалады әрі мұның сол
жағындағы қисықсызықты интеграл бар
сонда және тек сонда, егер оның оң
жағындағы анықталған интеграл бар
болса.Мысалы, егер AB қисығы
(1)
теңдігі орындалады әрі мұның сол
жағындағы қисықсызықты интеграл бар
сонда және тек сонда, егер оның оң
жағындағы анықталған интеграл бар
болса.Мысалы, егер AB қисығы
 теңдеуі
арқылы берілсе, онда (1) формула
теңдеуі
арқылы берілсе, онда (1) формула
 түрінде
жазылады. Ескерту.
Бірінші текті қисықсызықты интегралдың
екі айнымалы үшін анықталған анықтамасы
сөзбесөз кеңістіктік қисық бойында
берілген функция үшін де көшіріледі:
егер AB қисығы
түрінде
жазылады. Ескерту.
Бірінші текті қисықсызықты интегралдың
екі айнымалы үшін анықталған анықтамасы
сөзбесөз кеңістіктік қисық бойында
берілген функция үшін де көшіріледі:
егер AB қисығы
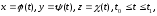 параметрлік
теңдеулері арқылы берілсе, онда осы
қисық арқылы алынған бірінші текті
қисықсызықты интеграл
параметрлік
теңдеулері арқылы берілсе, онда осы
қисық арқылы алынған бірінші текті
қисықсызықты интеграл

формуласы арқылы анықталған интегралға келтіріледі.
12) Бірінші текті қисық сызықты интегралды есептеу.
1. Қисық теңдеуі айқын түрде берілген жағдай.
2. Қисық теңдеуі полярлық координаттарда берілген жағдай.

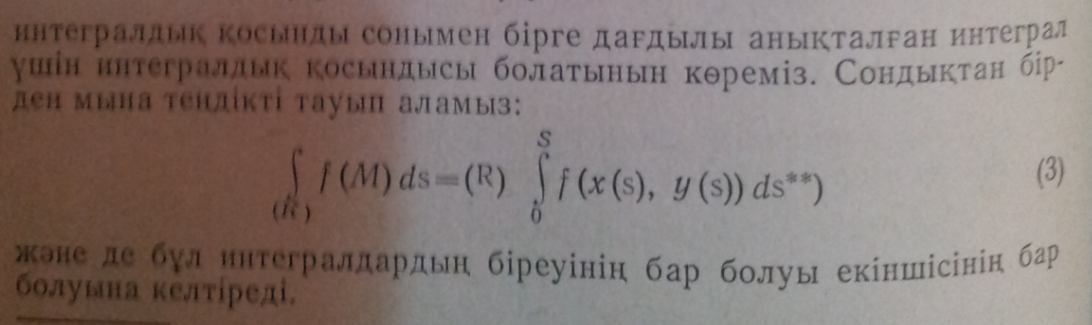



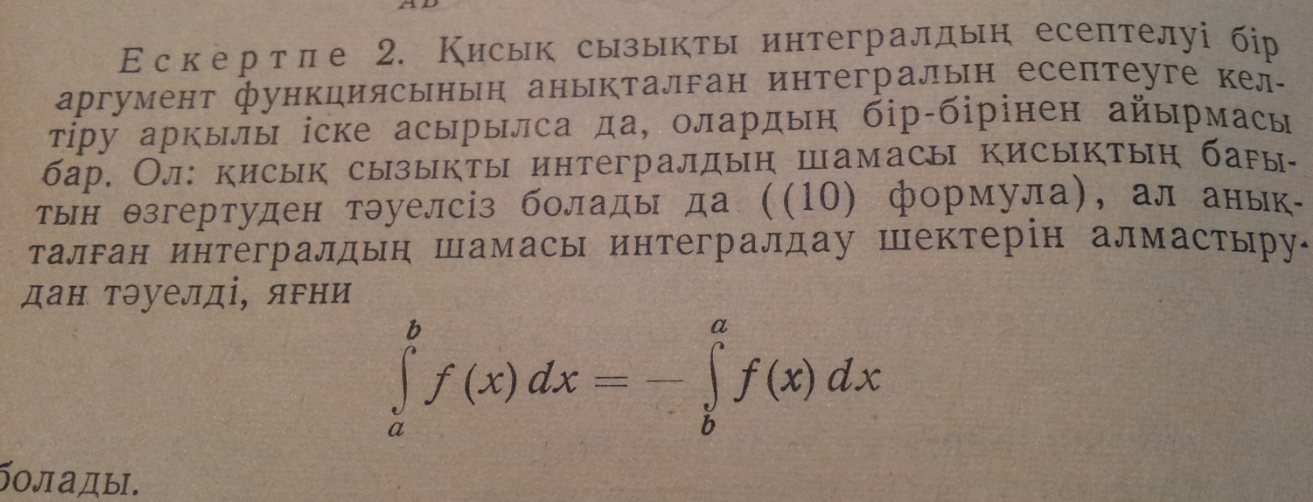
13) Екінші текті қисық сызықты интеграл.
1. Екінші текті қисық сызықты интеграл ұғымына келтіретін есеп – жазық күш өрісінің жұмысы туралы есеп.
2. Екінші текті қисық сызықты интеграл анықтамасы.
3. Екінші текті қисық сызықты интеграл бар болуы (дәлелдеуімен).


14) Екінші текті қисық сызықты интегралды есептеу
1. Қисық теңдеуі айқын түрде берілген жағдай
2. Қисық теңдеуі параметрлік түрде берілген жағдай
Айталық,
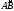 жазықтықтың жатық қисығы, ал
жазықтықтың жатық қисығы, ал
 осы
қисық бойында анықталған вектор-функция
болсын. Бұл қисықты координаттары
осы
қисық бойында анықталған вектор-функция
болсын. Бұл қисықты координаттары
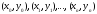 болатын
болатын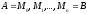 нүктелері
арқылы бөліктерге бөлейік те
нүктелері
арқылы бөліктерге бөлейік те
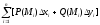 (11)
(11)
қосындысын
түзейік, мұндағы
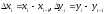 .
Егер
.
Егер
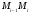 доғалары ұзындықтарының максимумы
нөлге ұмтылғанда (11) қосынды ақырлы бір
шекке ұмтылса, онда бұл шекті F=(P,Q)
вектор-функциясының AB қисығы бойынша
екінші
текті қисықсызықты интегралы
деп атайды да
доғалары ұзындықтарының максимумы
нөлге ұмтылғанда (11) қосынды ақырлы бір
шекке ұмтылса, онда бұл шекті F=(P,Q)
вектор-функциясының AB қисығы бойынша
екінші
текті қисықсызықты интегралы
деп атайды да
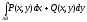 (12)
(12)
арқылы белгілейді.
Екінші текті қисықсызықты интеграл бірінші текті қисықсызықты интегралға оңай келтірілетінін мына теоремадан көреміз:
1-теорема. Егер AB жатық қисығы
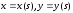 (13)
(13)
теңдеуі арқылы берілген, ал F=(P,Q) вектор-функциясы осы қисықта анықталған және шектеулі болса, онда
 (14)
(14)
теңдігі
орындалады. Мұнда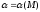 арқылы AB қисығына М нүктесінде жүргізілген
жанама менхосінің
оң бағыты арасындағы бұрыш белгіленген.
Сонымен бірге, екінші текті қисықсызықты
интеграл бар, егер (14) оң жағындағы
бірінші текті қисықсызықты интеграл
бар болса.
арқылы AB қисығына М нүктесінде жүргізілген
жанама менхосінің
оң бағыты арасындағы бұрыш белгіленген.
Сонымен бірге, екінші текті қисықсызықты
интеграл бар, егер (14) оң жағындағы
бірінші текті қисықсызықты интеграл
бар болса.
Дәлелдеу. Ең алдымен
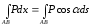
Теңдігін
дәлелдейік.
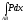 интегралы
анықтама
бойынша
интегралы
анықтама
бойынша түріндегі
қосындының
шегі.
Осы
қосындыны
AB қисығының
дәл
сол
бөліктеуінде
түріндегі
қосындының
шегі.
Осы
қосындыны
AB қисығының
дәл
сол
бөліктеуінде
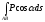 интегралына
сәйкес
интегралына
сәйкес

Интегралдық қосындысымен салыстырамыз. Егер x=x(s) болса, онда АВ қисығының әр бір М нүктесінде
 =
=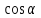 (M),
(M), 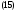
демек,
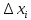 =
=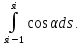
Eнді бұған орта мән туралы теореманы қолдансақ
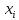 =
= )
)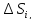
мұнда
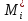 арқылы
арқылы
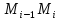 доғасының белгілі бір нүктесін
белгіледік.Сонда
доғасының белгілі бір нүктесін
белгіледік.Сонда
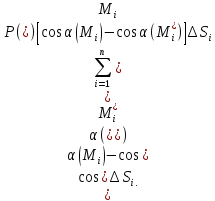
Жатық
қисық
бойында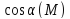 үзіліссіз,
ал
қисық
тұйық
шектеулі
жиын
болғандықтан
бұл
функция
бір
қалыпты
үзіліссіз.
Демек, кезкелген
үзіліссіз,
ал
қисық
тұйық
шектеулі
жиын
болғандықтан
бұл
функция
бір
қалыпты
үзіліссіз.
Демек, кезкелген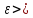 0
саны үшін АВ қисығының жеткілікті майда
бөліктері үшін
0
саны үшін АВ қисығының жеткілікті майда
бөліктері үшін
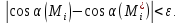
Сонда
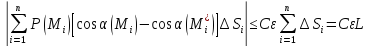
мұндағы
C=sup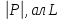 арқылы АВ қисығының ұзындығы белгіленген.
Мұнан
арқылы АВ қисығының ұзындығы белгіленген.
Мұнан
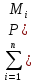 )
)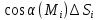
Интегралдық қосындысының шегі бар болса,онда
 )
)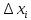
Қосындысының да сол шекке ұмтылатынын көреміз. Дәл осылай
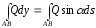
теңдігіндедәлелдейміз.Теорема дәлелденді.
Мысалы,егер АВ қисығы
y=y(x),
x (20)
(20)
айқын теңдеуі арқылы берілсе, онда (19) формула
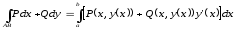 (21)
(21)
түріне
көшеді. Егер АВ қисығы y=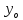 горизонталь
түзуінің кесіндісі болса, онда оның
бойында
горизонталь
түзуінің кесіндісі болса, онда оның
бойында
 және
және
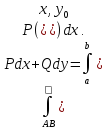
Қисық теңдеуі параметрлік түрде берілген жағдай
Егер АВ жатық қисығы
x=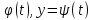 (18)
(18)
теңдеулері арқылы берілген, ал F=(P,Q) осы қисықта берілген вектор функция болса,онда
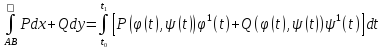 (19)
(19)
және
сол жақтағы интеграл бар, егер оң жақтағы
интеграл бар болса әрі t параметрінің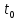 мәні А нүктесіне сәйкес, ал
мәні А нүктесіне сәйкес, ал
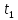 мәні В нүктесіне сәйкес.
мәні В нүктесіне сәйкес.
ЕгерАВқисығы
x=x(y),y теңдеуіарқылыберлсе,онда
теңдеуіарқылыберлсе,онда
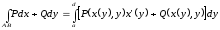 (22)
(22)
1
ескерту.
Вектор функцияның жазық қисық бойымен
алынған екінші текті қисық сызықты
интеграл анықтамасы кеңістік жағдайы
үшінде сөзбе сөз көшіріледі.  =(P,Q,R)
вектор функциясының кеңістік АВ қисығы
бойынша екінші текті қисықсызықты
интегралын
=(P,Q,R)
вектор функциясының кеңістік АВ қисығы
бойынша екінші текті қисықсызықты
интегралын

немесе
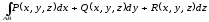 (23)
(23)
15) Тұйық контур бойынша екінші текті қисық сызықты интеграл.
1. Грин формуласы (дәлелдеуімен).
2. Екінші текті қисық сызықты интеграл көмегімен жазық фигура ауданын есептеу.


