Особенности движения частиц над потенциальной ямой
• Мы рассмотрели случай, когда полная энергия частицы Е была меньше высоты стенок потенциальной ямы (финитное движение). В этом случае размерный эффект проявляется в квантовании энергии и волнового вектора частицы.
• В случае, когда энергия частицы превосходит высоту стенок потенциальной ямы (En > Uj, рис.9.4), движение частицы является инфинитным. Однако, как и в случае
движения над потенциальным барьером, здесь возможно отражение частиц от областей с резким изменением потенциала (в данном случае от краёв ямы) и даже своеобразный резонансный захват пролетающих над ямой частиц.
• Если частица движется вдоль оси X, то, достигая потенциальной ямы, она испытывает действие сил. При этом частица либо отразится, либо "пройдет" над потенциальной
ямой. В областях 1 и 2 (рис.9.4а) решение уравнения (9.2) в данном случае имеет вид |
|||
Ψj (x)= Aj exp(iK j x)+ Bj exp(−iK j x), K1 = |
2m(E −U1 ) h, |
K2 = 2mE h, |
(9.49) |
• В области 3 (x>W/2) решение имеет вид уходящей от ямы волны |
|
||
Ψ3 (x)= A3 exp(iK3 x), |
K3 = 2m(E −U2 ) |
h |
(9.50) |
• Чтобы вычислить коэффициенты прохождения и отражения (9.13, 9.14), надо выразить амплитуды A3 и В1 через амплитуду падающей волны A1. Для этого используем условие непрерывности волновой функции и потока частиц при X = ±W/2. В результате получим
|
|
|
D = 4K K 2K |
3 |
Z; |
|
|
K22 ] Z ; |
(9.51) |
||
|
|
|
1 |
2 |
|
+ K3 )2 |
|
||||
R = [(K12 − K22 ) (K32 − K22 ) sin2 |
(K2W )+ (K1 |
(9.52) |
|||||||||
Z = (K 2 |
− K 2 ) (K 2 |
− K 2 ) sin2 (K W )+ (K |
1 |
+ K |
)2 K 2 |
; |
|
||||
1 |
2 |
3 |
2 |
|
|
2 |
3 |
2 |
|
|
|
Особенности движения частиц над потенциальной ямой
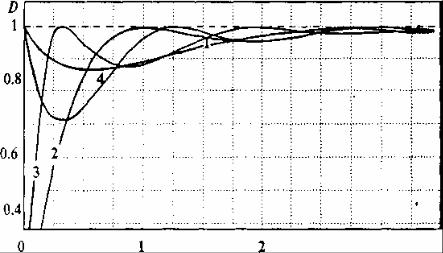
•Согласно (9.51), как и в случае потенциального барьера при прохождении частиц над потенциальной ямой коэффициент прохождения осциллирует с увеличением энергии частицы
•(рис.9.5). В обоих случаях осцилляции имеют одну и ту же физическую природу. Квазиклассически их можно трактовать как результат интерференции электронных волн, отраженных от скачков потенциала на границах барьера или ямы. Однако, как показывает сравнение рис.9.3 и 9.5, при близком качественном характере зависимостей имеются и заметные различия. Так, при равных значениях ширин и скачков потенциала барьера и ямы размах осцилляции коэффициента D при прохождении частиц над барьером больше, чем при прохождении над ямой.
•На первый взгляд .движение электронов над потенциальной ямой оказывается еще менее пригодным для наблюдения и использования осцилляции коэффициента прохождения.
Однако в данном случае заметные осцилляции могут наблюдаться при сравнительно небольших энергиях частицы, что улучшает условия их наблюдения [3].
E2/U0
Рис. 9.5 Зависимость коэффициента прохождения над потенциальной ямой от энергии:
1 – U0/V1 = 1, 2 - U0/V1 = 2, 3 - U0/V1 = 3, 4- U0/V1 =4
Энергетические состояния
впрямоугольной квантовой яме сложной формы
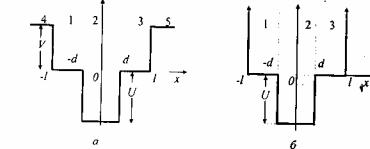
•Возможность получения слоев с произвольным профилем изменения состава позволила для улучшения характеристик приборов использовать структуры с КЯ сложной формы. Так,для создания нового поколения резонансно-туннельных диодов и гетеролазеров с раздельным электронным и оптическим ограничением [8] применяются структуры с прямоугольными КЯ, в центре которых имеется дополнительный провал (рис.9.6а)
•Рассмотрим влияние дополнительного провала на
энергетический спектр КЯ с бесконечно высокими стенками (рис.9.6б) [5]. При анализе учтем, что провал получен изменением состава твердого раствора, и, следовательно, в
области провала (-d≤x≤d) эффективная масса электрона m1 может отличаться от эффективной массы m2 в прилегающих областях (d≤|x|≤l).
Рис.9.6 - Энергетическая диаграмма КЯ с дополнительным потенциальным провалом
•В случае, когда эффективная масса зависит от координаты, одномерное уравнение Шредингера
|
может быть представлено в виде − h2 d 1 d |
+U (x) Ψ = EΨ |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(9.53) |
||
|
2 dx m(x) dx |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||
• |
Для областей 1 и 3 (d≤|x|≤l) (9.53) принимает вид |
h2 |
|
|
|
d 2 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
+0 Ψ = EΨ |
(9.54) |
||
|
|
|
|
|
|
|
|
|
2m |
|
|
dx2 |
||||||
|
Аналогично для области (-d≤x≤d) имеем |
|
1 |
|
|
|
|
|
|
|
|
|||||||
• |
|
h2 |
|
|
|
d 2 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
− |
|
|
|
−U |
Ψ = EΨ |
(9.55) |
|||
|
|
|
|
|
|
|
|
|
2m |
|
dx2 |
|
||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
Энергетические состояния
в прямоугольной квантовой яме сложной формы
• Найдем положение разрешенных энергетических уровней для E>0 (т.е. попадающих в широкую часть
КЯ). В этом случае волновая функция во всех трех областях может быть представлена в виде |
|||
Ψj (x)= Aj exp(iK j x)+ B2 exp(−iK j x), |
|
j =1,2,3; |
|
K1,3 = 2m1E h, |
K2 = 2m(E +U ) |
h |
(9.56) |
|
|||
•Для нахождения коэффициентов Аj и Bj , как обычно воспользуемся условиями, обеспечивающими непрерывность волновой функции (непрерывность плотности частиц) и плотности потока частиц.
Тогда при |х| = d имеем, что |
и |
1 dΨ1,3 |
= |
1 |
dΨ2 |
|
|
|||||
Ψ1,3 = Ψ2 |
|
|
||||||||||
m1 |
|
|
dx |
m2 |
dx |
|
(9.57) |
|||||
|
|
|
|
|||||||||
• Кроме того, так как стенки КЯ бесконечно высокие, |x| = 1 |
|
Ψ1,3 |
= 0 |
|||||||||
|
(9.58) |
|||||||||||
• Используя граничные условия (9.57) и (9.58), получим два уравнения: |
|
|||||||||||
tg{K (l − d )}= m2 |
K1 |
ctg(K |
d ), |
|
(9.59) |
|||||||
|
|
|||||||||||
1 |
|
m1 |
K2 |
|
|
2 |
|
|
||||
|
|
|
|
|
|
|
|
|||||
tg{K (l − d )}= m2 |
K1 |
tg(K |
d ), |
|
(9.60) |
|||||||
|
|
|||||||||||
1 |
|
m1 |
K2 |
|
2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||||
•из которых первое определяет разрешенные К (а следовательно, и Еn) для четных состояний, а второе - для нечетных.
•Анализ выражений (9.59) и (9.60) позволяет выявить влияние провала и различия эффективных масс на положение разрешенных уровней энергии. Так, для основного (нижнего) четного состояния из (9.59)
получаем |
|
|
π |
|
|
K2 |
|
|
|
K1l = F0 , |
F0 |
= |
+K1d − arctg |
m1 |
|
tg(K2d ) |
(9.61) |
||
2 |
|
K1 |
|||||||
|
|
|
m2 |
|
|
|
|||
Энергетические состояния
впрямоугольной квантовой яме сложной формы
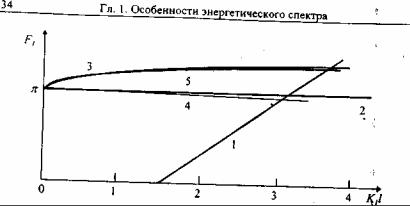
•На рис.9.7 представлено решение уравнения (9.61) графическим методом.
•Разрешенные значения К1, при известной ширине КЯ (2l) определяются точками пересечения прямой 1 (соответствующей правой части уравнения (9.61)) с зависимостями F0(K1l) (кривые 2-5)
•Анализ (9.61) и приведенных зависимостей показывает, что для
основного четного состояния: 1 - уменьшение эффективной массы т2 сдвигает разрешенный уровень энергии в область больших энергий; 2- увеличение
ширины d и глубины U провала понижает разрешенный уровень энергии; 3- результирующее смещение уровня энергии определяется суперпозицией данных эффектов, при этом влияние эффективной массы обычно слабее.
Так, при m2 |
→ 0 аргумент у arctg в (9.61) стремится к |
||||||
|
|
2 |
|
m1 |
2d |
|
|
|
m1 |
K2 |
|
(E +U ) |
|||
|
|
|
K |
d |
= h2 |
K |
|
|
m |
||||||
|
2 |
1 |
|
|
1 |
|
|
Рис.9.7. Графическое решение уравнения (9.61):
1 – K1l; 2,3,4 и 5 – F0(K1l); 2 – m2 = m1 и U = 0; 3 – m2 < m1 и U = 0; 4 - m2 < m1 и U ≠ 0;
5 - m2 = m1 и U ≠ 0
•т.е. влияние m2 на решение уравнения (9.61) вообще исчезает, а влияние d и U остается.
•Увеличивая ширину и глубину провала, можно "выдавить" основной четный уровень из широкой части КЯ в провал. В этом случае кривые F0(K1l) не будут пересекать прямую 1 (рис.9.7) при (K1l)> 0, а следовательно, производная функции F0(K1l) по переменной (K1l) в точке (K1l) =0 станет меньше единицы. Отсюда следует, что условие существования основного четного уровня в широкой части
потенциальной ямы имеет вид |
|
m |
E |
|
|
U |
|
|
|
|
|
h2 |
(9.62) |
||
d 1 |
+ |
2 |
|
d ctg |
E |
|
|
> l, |
E |
|
= |
2m d 2 |
|||
|
|
m |
U |
|
d |
|
|
|
|
d |
|
|
|||
|
1 |
|
|
|
|
|
|
|
|
|
2 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
•Анализ (9.62) показывает, что увеличение d, U, m1 или т2 способствует выдавливанию основного четного уровня в провал.
Энергетические состояния
впрямоугольной квантовой яме сложной формы
•Рассмотрим теперь влияние параметров системы на положение первого возбужденного (нечетного) состояния. Как следует из (9.60), выражение для определения разрешенных значений К в этом случае может быть
представлено в виде |
|
m1 |
|
K2 |
tg(K |
d ) |
||||
K l = F |
, |
F |
=π +K d − arctg |
|
||||||
|
|
|||||||||
1 1 |
|
0 |
1 |
|
|
K1 |
2 |
(9.63) |
||
|
|
|
|
m2 |
|
|
|
|||
Решение уравнения (9.63) графическим методом
показано на рис.9.8 |
Рис.9.8. Графическое решение |
|
• Анализ показывает, что и в этом случае |
уравнения (9.63): |
|
1 – K1l; 2,3,4 и 5 – F0(K1l); 2 – m2 = m1 и U = 0; 3 |
||
уменьшение m2 увеличивает разрешенное |
||
– m2 < m1 и U = 0; 4 - m2 < m1 и U ≠ 0; |
||
значение энергии, а рост d и U –уменьшает. |
5 - m2 = m1 и U ≠ 0 |
Однако в данном случае ослабляется роль U. Так, устремляя m2 к нулю, видим, что аргумент arctg в
(9.63) стремится к |
m2 |
|
K1 |
|
|
m2 |
|
|
|
|
|
|
|
|
|
= |
|
K1d |
|
|
|
|
|
|
|
||||
|
|
|
K2 |
K2d |
m1 |
, т.е. влияние U исчезает. |
|||
|
m1 |
|
|
|
|
||||
•Различное влияние U и m2 на положение основного и первого возбужденного состояния связано с различным видом волновых функций, соответствующих этим состояниям. Если для основного состояния в области провала велико значение |Ψ|2 и мало значение |dΨ/dx|2 , то для первого
возбужденного, наоборот, велико |dΨ/dx|2 , но мало |Ψ|2 . Так как средняя энергия в данном состоянии,
|
|
+∞ |
h2 |
|
|
dΨ |
|
2 +∞ |
||||
|
|
|
|
|||||||||
|
|
= ∫ |
|
|
dx + ∫U (x) |
|
Ψ |
|
2dx |
|||
|
E |
|
|
|
|
|||||||
|
2m |
|
dx |
|
||||||||
|
|
−∞ |
|
|
−∞ |
|||||||
то оказывается, что в основном состоянии средняя энергия будет более "чувствительна" к наличию и величине провала, а в первом возбужденном состоянии - к значению m2.
Энергетические состояния
впрямоугольной квантовой яме сложной формы
•В результате оказывается, что можно создать структуру, у которой наличие слоя с меньшей
эффективной массой приведет к понижению энергии основного и повышению энергии возбужденного состояния, т.е. энергетический зазор между этим( уровнями станет больше,
чем в случае простой КЯ, что, например, используют для увеличения контрастности ВАХ резонансных туннельных диодов.
•Реально мы имеем дело с потенциальными ямами, стенки которых имеют конечную высоту (рис.9.6а).
Рассмотрим влияние конечной высоты cтенок на разрешенные значения энергии основного и первого возбужденного состояния КЯ при наличии провала.
•В этом случае необходимо дополнительно учесть возможное проникновения частицы под барьеры (т.е. в области 4 и 5, си рис.9.6а). Решение уравнения (9.53) для этих областей (|x|≥l) можно записать
в виде |
Ψ |
= C |
|
exp{− β( |
|
x |
|
−l)}, |
β2 = |
2m3 |
(V − E) |
(9.64) |
|
|
|
||||||||||
|
|
|
|
|
||||||||
|
4,5 |
|
4,5 |
|
|
|
|
|
|
h2 |
|
|
|
|
|
|
|
|
|
|
|
•Учитывая граничные условия при x = ±d и х = ±l, можно бы бы записать систему алгебраических уравнений, определяют разрешенные значения К и Е. Однако при этом пришлось бы искать совместное решение системы из восьми уравнений. Для упрощения расчетов лучше учесть
симметрию задачи и вместо граничных условий для х<0 использовать граничные условия при х=0. |
||||||||||||
При этом для четных состояний получим |
Ψ′(0)= |
0 |
|
|
|
|
|
|
|
|
(9.65) |
|
и для нечетных состояний ,соответственно |
2 Ψ (0)= 0 |
Ψ2 (d )= Ψ3 (d ), |
1 |
|
1 |
|
(9.66) |
|||||
|
|
2 |
|
|
Ψ2′ = |
Ψ3′ |
|
|||||
Учитывая (9.65), (9.66) и граничные условия при x=d, |
|
(9.67) |
||||||||||
|
|
|
||||||||||
и при x=l |
Ψ (l)= Ψ (l), |
|
1 |
Ψ′ = |
1 |
Ψ′ |
m2 |
m1 |
(9.68) |
|||
|
|
|
|
|
|
|
||||||
|
3 |
5 |
|
m1 |
3 |
5 |
|
|
|
|
|
|
|
|
|
|
|
m3 |
|
|
|
|
|
||
•получим две системы по пять уравнений, решения которых и oпределят разрешенные значения К и Е для четных и нечетных состояний.