
прикладная мех задачи
.pdf
∑Fkx = RAx + RCx =0, |
(3.1) |
∑Fky = RAy + RB + RCy − P =0, |
(3.2) |
∑mA (Fk )= RB AB + RCy AC − P AE − M =0. |
(3.3) |
Можно было бы вместо второго уравнения равновесия составить сумму моментов всех сил относительно точки С. В это уравнение вошли бы только две неизвестные силы RAx и RВ, так как линии действия остальных, неизвестных сил пересекаются в точке С. Однако в обоих случаях уравнение (3.1) является независимым от остальных уравнений и содержит два неизвестных; уравнения (3.2) и (3.3) связаны между собой и содержат три неизвестных.
Таким образом, из полученной системы ни одно из неизвестных не может быть определено. Рассмотрим поэтому равновесие второй балки
CD (рис. 3.3).
На балку действует одна активная сила Q. Применяя закон освобождаемости от связей, заменим действие шарнира С и опоры D реакциями связей.
Реакция RD направлена по вертикали, перпендикулярно к горизонтальной плоскости, на которую опираются катки. Реакция шарнира С неизвестна по модулю и направлению. На основании закона равенства действия и противодействия составляющие этой реакции равны по модулю составляющим реакции шарнира, приложенным к балке АС, и направлены в прямо противоположные стороны (рис. 3.3).
Таким образом, имеем свободное твердое тело – балку CD, находящуюся в равновесии под действием пяти сил. Составим уравнения равновесия, выбрав оси координат с началом в точке С; ось абсцисс направим по балке вправо, ось
ординат – вертикально вверх. Имеем |
|
∑Fkx = −RCx = 0, |
(3.4) |
∑Fky = RD −Q − RCy = 0, |
(3.5) |
∑mC (Fk )= RD CD −Q CH =0. |
(3.6) |
Вэтих трех уравнениях равновесия только одна новая неизвестная RD.
Авсего в шести уравнениях равновесия шесть неизвестных. Из уравнений
(3.4) и (3.1) следует
RCx = RAx =0 .
Из уравнения (3.6) находим
RD =Q CHCD =120 24 =60H ,
аиз(3.5) получаем
21
RCy = RD −Q =60 −120 = −60H.
Знак минус показывает, что в действительности направления составляющих Rcy и RCy′ противоположны принятым на рисунке.
Далее, из (3.3) имеем
RB = P AEAB + ABM − RCy ACAB =80 64 + 2006 + 60 96 =176,6H
и, наконец, из (3.2) находим
RAy = P − RB − RCy =80 −176,6 + 60 = −36,6H.
Знак минус указывает, что и реакция RAy направлена не вверх, как предполагалось, а по вертикали вниз.
Эта задача может быть решена и другим путем. Можно рассмотреть равновесие балки CD и равновесие всей двухпролетной балки ABCD. Из уравнений равновесия для балки CD (3.4), (3.5) и (3.6) легко находятся реакции шарнира С и опоры D, так как эти три уравнения содержат три неизвестных: RСx, RСy, RD.
Рассматривая далее равновесие двухпролетной балки ABCD, составим три уравнения равновесия, из которых определяются три оставшихся неизвестных:
RAx, RAy, RB.
3.2. Определение реакций составной конструкции (задание С 4 [8])
|
|
Дано: схема конструкции |
(рис. |
3.4); |
|
|
|
Р1 = 5 кН, Р2 = 7 кН; М = 2 кН м; q = 2 кН/м; |
|||
|
|
α = 60°. |
|
|
|
|
|
Определить реакции в опорах и в промежу- |
|||
|
|
точном шарнире составной конструкции. |
|
||
|
|
Решение. Рассмотрим систему уравновеши- |
|||
|
|
вающихся сил, приложенных ко всей конструкции |
|||
Рис. 3.4. |
|
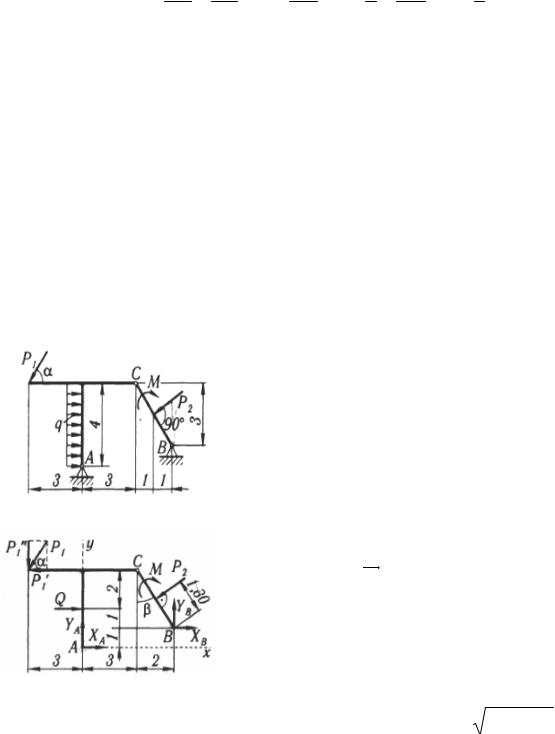
(рис. 3.5). |
|
|
|
|
|
Составим уравнение моментов сил отно- |
|||
|
|
сительно точки В. Для упрощения вычисления |
|||
|
|
момента силы Ð1 разложим ее на вертикальную |
|||
|
|
и горизонтальную составляющие: |
|
|
|
|
|
Р1′ = Р1 cos 60° = 2,5 кН; |
|
|
|
Рис. 3.5. |
|
Р1′′= Р1 sin 60° = 4,33 кН; |
|
|
|
′ |
′′ |
2 |
2 |
= 0, |
(3.7) |
∑MiB = 0; P1 3 |
+ P1 8 |
−Q 1 −YA 5 + X A 1 − M + P2 1 +1,5 |
|
||
где Q = q 4 = 2 4 = 8 кН.
После подстановки данных и вычислений уравнение (3.7) получает вид
22
XA – 5YA = – 44,74 кН. |
(3.8) |
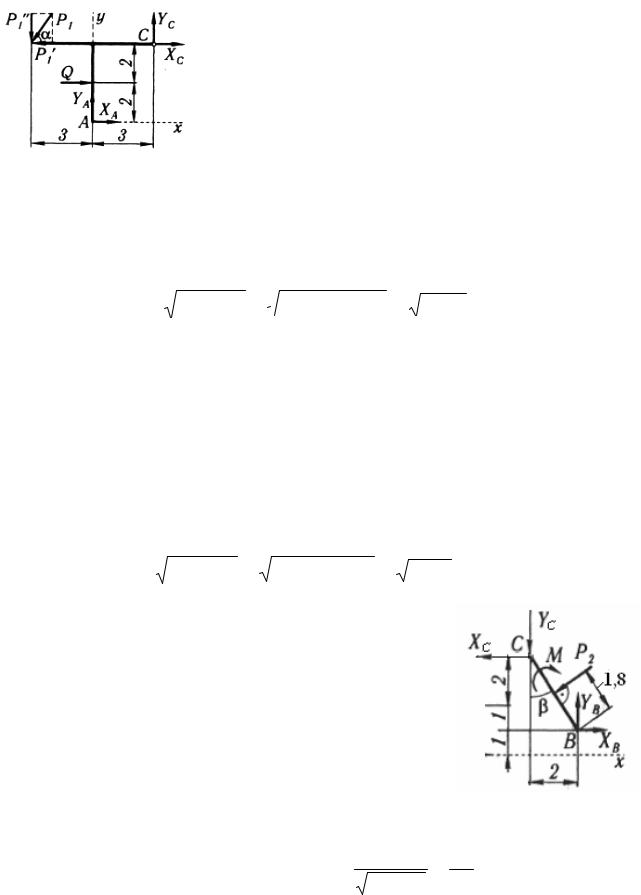
Второе уравнение с неизвестными ХА и YA получим, рассмотрев систему уравновешивающихся сил, приложенных к части конструкции, расположенной левее шарнира С (рис. 3.6):
|
∑M iC = 0; P1′′ 6 +Q 2 + X A 4 −YA 3 = 0, |
||
Рис. 3.6. |
откуда |
4XA – 3YA = – 41,98 кН. |
(3.9) |
Решая систему уравнений (3.8) и (3.9), находим: |
|
||
|
ХА = – 4,44 кН, |
YA = 8,06 кН. |
|
Модуль реакции опоры А при шарнирном соединении в точке С равен
RA = X A2 +YA2 =  4,442 +8,062 = 84,67 = 9,2 кН.
4,442 +8,062 = 84,67 = 9,2 кН.
Определим составляющие реакции в промежуточном шарнире С. Составим уравнение равновесия части конструкции, расположенной левее шарнира С (рис. 3.6) в виде равенства нулю суммы проекций сил на ось х и на ось у:
∑ Xi = 0 , |
− P1′+ X A +Q + XC = 0 , |
XC = P1′− X A −Q , |
|||
|
|
|
ХС = 2,5 + 4,44 – 8 = – 1,06 кН; |
||
∑Yi = 0, |
− P1′′+YA +YC = 0 , |
YC = P1′′−YA = 4,33 – 8,06 = – 3,73 кН. |
|||
Модуль реакции в промежуточном шарнире С равен |
|||||
R |
= |
X 2 |
+Y 2 = 1,062 |
+3,732 = |
15,03 = 3,88 кН. |
С |
|
С |
С |
|
|
Для определения реакции в опоре В рассмотрим равновесие сил, приложенных к части конструкции правее шарнира С (рис. 3.7). Реакции ХС и YC уже определены. На схеме рис. 3.7 реакции ХС и YC направлены противоположно, чем эти же реакции на схеме рис. 3.6 (равенство сил действия и противодействия).
Используем уравнение равновесия в виде равенства нулю суммы проекций всех сил на ось х:
∑ Xi = 0 , − XC + X B − P2 cos β = 0, откуда |
|
|||||
X |
B |
= X |
C |
+ P cos β , |
cos β = |
3 |
|
|
2 |
22 |
+32 |
||
|
|
|
|
|
||
Рис. 3.7
= 3,63 = 0,833;
ХВ = – 1,06 + 7·0,833 = – 1,06 + 5,83 = 4,77 кН.
23
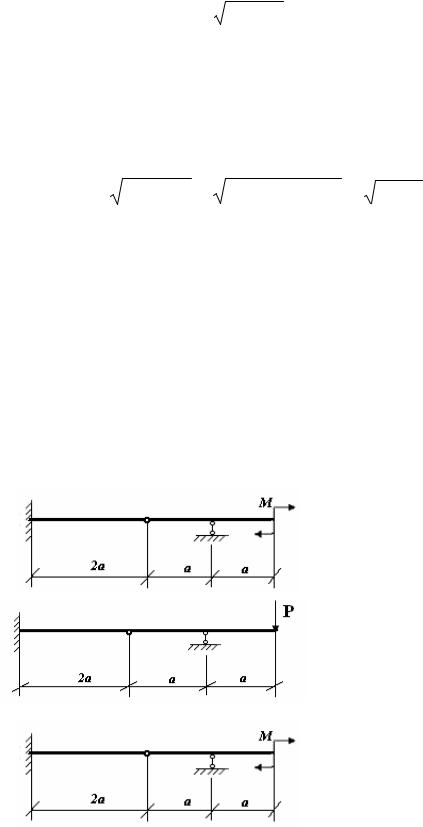
Используем уравнение равновесия в виде равенства нулю суммы моментов сил относительно точки С:
|
|
∑MiC |
= 0, |
YB 2 + X B 3 − M − P2 hp = 0, |
(3.10) |
||
|
h = BC −1,8 = |
22 +32 – 1,8 = 3,6 – 1,8 = 1,8 м, |
|
||||
|
|
p |
|
|
|
|
|
где hp – плечо силы Р2 относительно точки С. |
|
|
|||||
В результате из (3.10) с учетом, что ХВ = 8, 3 кН, получим |
|
||||||
|
|
YB 2 + 4,77 3 −2 −7 1,8 = 0, |
YB = 0,15 кН. |
|
|||
Модуль реакции опоры В равен |
|
|
|||||
R |
В |
= X 2 |
+Y 2 |
= |
4,772 +0,1452 = |
22,77 = 4,78 кН. |
|
|
В |
В |
|
|
|
|
|
Для проверки правильности выполненных расчетов возвратимся к схеме сил и реакций в опорах на рис. 3.5 и воспользуемся уравнениями равновесия в
виде: |
− P1′+ X A +Q + X В − Р2 cos β = 0 , |
|
|
|
||||||
∑ Xi = 0 , |
|
|
|
|||||||
– 2,5 – 4,44 + 8 + 4,77 – 7· |
|
3 |
|
= 0, – 12,77 + 12,77 =0; |
|
|
||||
3,6 |
|
|
||||||||
|
|
|
|
|
|
|
|
|||
∑Yi = 0, |
− P1′′+YA +YВ − Р2 sin β = 0 , |
|
|
|
||||||
– 4,33 + 8,06 + 0,15 – 7· |
2 |
|
= 0, – 8,21 + 8,21 = 0. |
|
|
|||||
3,6 |
|
|
|
|||||||
3.3. Тестовые задания |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
1. |
Момент в заделке равен… |
|||
|
|
|
|
|
|
1) |
0,5 М |
|
|
|
|
|
|
|
|
|
2) |
М |
|
|
|
|
|
|
|
|
|
3) |
1,5 М |
|
|
|
С 1 |
|
|
|
|
|
4) |
2М |
|
|
|
|
|
|
|
|
|
2. Момент в заделке равен… |
||||
|
|
|
|
|
|
1) |
0,5 Ра |
|
|
|
|
|
|
|
|
|
2) |
Ра |
|
|
|
|
|
|
|
|
|
3) |
1,5 Ра |
|
|
|
С 2 |
|
|
|
|
|
4) |
2 Ра |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
3. Сила в заделке равна… |
|
|
||
|
|
|
|
|
|
1) |
М |
2) |
2М |
|
|
|
|
|
|
|
а |
а |
|||
|
|
|
|
|
|
|
|
|||
С 3 |
|
|
|
|
|
3) |
М |
4) |
2М |
|
|
|
|
|
|
|
2а |
|
3а |
||
24 |
|
|
|
|
|
|
|
|
|
|
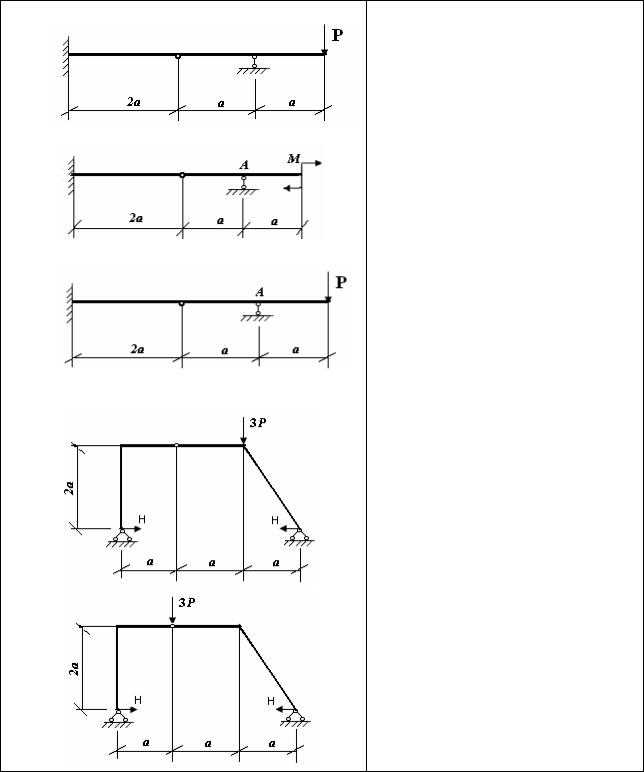
4. Сила в заделке равна: |
|
1) |
0,5 Р |
2) |
Р |
3) |
2 Р |
4) |
2,5 Р |
С 4 |
|
|
|
|
|
|
|
5. Реакция в опоре А равна… |
|||||
|
1) |
М |
2) |
М |
||
|
|
|
|
а |
||
|
3) |
2 М |
4) |
2М |
|
|
С 5 |
а |
|||||
|
|
|
||||
|
|
|
|
|
||
|
6. Реакция в опоре А равна… |
|||||
|
1) |
Р |
|
|
|
|
|
2) |
2 Р |
|
|
|
|
С 6 |
3) |
3 Р |
|
|
|
|
4) |
4 Р |
|
|
|
||
|
|
|
|
|||
|
|
|||||
|
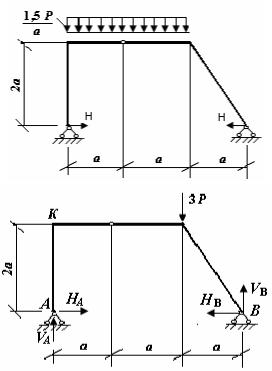
7. Горизонтальная реакция H в трех- |
|||||
|
шарнирной раме равна… |
|
|
|||
|
1) |
0,5 Р |
|
|
|
|
|
2) |
Р |
|
|
|
|
|
3) |
1,5 Р |
|
|
|
|
|
4) |
2 Р |
|
|
|
|
С 7 |
|
|
|
|
|
|
|
Горизонтальная реакция H в трех- |
|||||
|
шарнирной раме равна: |
|
|
|||
|
1) |
0,5 Р |
|
|
|
|
|
2) |
Р |
|
|
|
|
|
3) |
1,5 Р |
|
|
|
|
С 8 |
4) |
2 Р |
|
|
|
|
|
|
|
|
|
||
25
|
Горизонтальная реакция H в трех- |
|
|
шарнирной раме равна… |
|
|
1) |
0,5 Р |
|
2) |
Р |
|
3) |
1,5 Р |
|
4) |
2 Р |
С 10 |
|
|
|
Вертикальная реакция в опоре В пло- |
|
|
ской рамы равна… |
|
|
1) |
0,5 Р |
|
2) |
Р |
|
3) |
1,5 Р |
|
4) |
2 Р |
С 12 |
|
|
4. ОПРЕДЕЛЕНИЕ РЕАКЦИЙ ОПОР ТВЕРДОГО ТЕЛА (ПРОИЗВОЛЬНАЯ СИСТЕМА СИЛ)
4.1. Определение реакций опор нагруженного вала
Дано: схема нагружения вала, установленного на опорах (рис. 4.1).
На рис. 4.1, а изображена косозубая шестерня радиусом r, закрепленная на горизонтальном валу. Вал лежит в двух опорах: упорном подшипнике А и цилиндрическом подшипнике В.
26
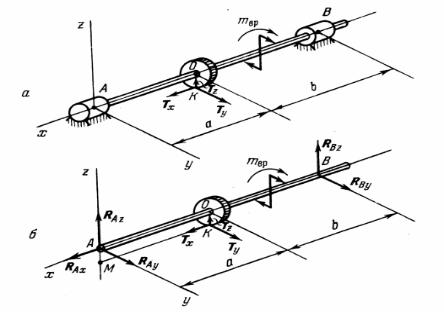
Рис. 4.1
Вточке К, расположенной в вертикальной плоскости симметрии шестерни,
кее зубу приложено давление Т со стороны другой шестерни, находящейся с ней в зацеплении (на рис. 4.1, а сила Т и вторая шестерня не изображены). Дав-
ление Т разложено на три составляющие Тх, Ту и Tz, которые соответственно параллельны осям координат х, у и z (начало координат взято в точке А, ось х направлена вдоль вала, ось z – по вертикали вверх, ось у – 1 так, чтобы вместе с осями х и z была образована правая система координат).
К валу, вращающемуся равномерно, приложена пара сил с вращающим моментом mвр так, что ее моменты относительно осей равны: mх = mвр,
mу = mz = 0.
Определить реакции опор А и В и вращающий момент mвр. Даны модули составляющих Тх, Ту и Tz давления Т на зуб шестерни. Размеры указаны на рисунке. Весом шестерни и вала пренебречь.
Решение
Для определения неизвестных реакций опор А и В и вращающего момента mвр рассмотрим равновесие вала с сидящей на нем шестерней. Под равновесием вала мы понимаем не только покой, но и его равномерное вращение, упомянутое в условии задачи.
К валу и шестерне приложены следующие активные силы, изображенные на рисунке: три составляющие Тх, Ту, Тz давления Т и пара сил, момент которой mх = mвр требуется определить (в данной задаче момент активной пары сил неизвестен).
Связями, наложенными на вал, являются две опоры: упорный подшипник А и подшипник В, мысленно отбросим связи и заменим их действия на вал реакциями. Подшипник В допускает перемещение вала вдоль оси х, поэтому
27
составляющая реакции вдоль оси х отсутствует, и нам остается изобразить лишь две составляющие RBy и RВz, перпендикулярные к оси вала.
Мы направляем на рис. 4.1, а эти составляющие в сторону возрастания соответствующих координат. Если в действительности направление какой-либо составляющей противоположно, то ответ окажется отрицательным.
Упорный подшипник А, в отличие от подшипника В, не допускает перемещения вала вдоль оси х. Поэтому в точке А мы изображаем все три состав-
ляющие RAx, RAу, RAz реакции.
Итак, нам предстоит рассмотреть равновесие свободного вала с шестерней под действием активных сил Тх, Ту, Tz и пары сил с моментом mх = mвр, а также составляющих реакций RAx, RAy, RAz, RBy, RBz. Все эти силы образуют пространственную систему сил, для которой надо записать шесть уравнений равновесия. Так как число алгебраических неизвестных также равно шести (mвр, RAx, RAy, RAz, RBy и RBz), то задача является статически определенной.
Составим уравнения проекций сил на оси декартовых координат х, у, z. Все силы либо перпендикулярны, либо параллельны этим осям. Поэтому их проекции равны нулю или модулю соответствующей силы. Так, силы Ту, Tz, RAy, RAz, RBy, RBz и пара сил перпендикулярны к оси х, и, следовательно, их проек-
ции на эту ось равны нулю. Из проекций на ось х лишь RAx |
и Тх отличны от |
нуля, причем обе проекции положительны. |
|
Итак, |
|
∑Fkx =Tx + RAx = 0. |
(4.1) |
Аналогично запишем уравнения проекций сил на оси у и z: |
|
∑Fky =Ty + RAy + RBy =0 , |
(4.2) |
∑Fkz =Tz + RAz + RBz =0. |
(4.3) |
Напомним, что проекция пары сил на любую ось равна нулю, ибо главный вектор пары сил равен нулю.
Переходим к составлению уравнений моментов сил относительно осей x, у, z. Предварительно заметим, что составление этих уравнений в данной задаче производится достаточно просто. Действительно, линии действия сил параллельны или пересекают оси координат и, значит, имеют моменты, равные нулю, либо силы лежат в плоскостях, перпендикулярных к осям и, следовательно, отпадает необходимость в проектировании этих сил на плоскости, перпендикулярные к осям.
При составлении уравнения моментов сил относительно оси х предварительно заметим, что силы RAx и Тх параллельны оси х, а линии действия сил RAy, RAz, Tz, RBy и RBz пересекают ось х. Следовательно, их моменты равны нулю. Значит, в уравнение моментов войдут лишь моменты силы Ту и пары сил.
По условию момент пары относительно оси х равен mвр , т.е.
mх = – mвр. |
(4.4) |
28
Знак минус взят, поскольку если смотреть с положительного направления оси х, то вращение, вызываемое парой, происходит по ходу часовой стрелки.
Сила Ту лежит в плоскости, перпендикулярной к оси х. Из точки О пересечения оси с плоскостью опускаем перпендикуляр ОК = r на линию действия Ту. Момент положителен, так как с конца оси x к ее началу видно, что сила Ту стремится повернуть тело вокруг точки О против часовой стрелки. Итак,
mх(Ту) = Ту r. |
(4.5) |
Используя формулы (4) и (5), запишем уравнение моментов |
|
∑mx (Fk )= −mâð +Ty r =0. |
(4.6) |
При составлении уравнения моментов относительно оси у заметим, что силы Ту, RAy, RBy параллельны оси у, а линии действия сил RAx и RAz пересекают ось у. Следовательно, моменты их равны нулю. Кроме того, по условию момент пары сил my равен нулю. Значит, отличными от нуля являются только моменты сил Тх, Tz и RBz.
Все эти силы лежат в плоскости xz, перпендикулярной к оси у. Плоскость xz пересекается с осью у в точке А. Поэтому из точки А опускаем перпендикуляры на линии действия сил Тх, Tz и RBz. Соответственно получим:
AM = r, АО = а и АВ = а + b.
Момент силы Тх отрицателен, так как с конца оси y к ее началу видно, что сила Тх стремится повернуть тело вокруг точки А по ходу часовой стрелки, а моменты сил Tz и RBz положительны, ибо они видны противоположно направленны-
ми. Итак, |
|
my (Tx )= −Tx r, my (Tz )=Tz a, my (RBz )= RBz (a +b). |
(4.7) |
Приняв во внимание формулы (4.7), запишем уравнение моментов относи- |
|
тельно оси у в виде |
|
∑my (Fk )= −Tx r +Tz a + RBz (a +b)=0. |
(4.8) |
При составлении уравнения моментов относительно оси z надо учесть, что силы Tz, RAz, RBz параллельны оси z, а линии действия сил Тх, RAx, RAy пересекают эту ось. Поэтому моменты этих сил относительно оси z равнынулю.
Кроме того, по условию момент пары сил относительно оси z также равен нулю. Значит, в уравнение войдут только моменты сил Ту и RBy. Сила Ту лежит в горизонтальной плоскости, перпендикулярной к оси z. Из точки М пересечения оси z с этой плоскостью опускаем перпендикуляр МК = АО = а на линию действия Ту. Момент силы Ту относительно оси z отрицателен, так как с конца оси z к ее началу видно, чтосила Ту стремится повернуть тело по ходу часовой стрелки. Значит,
mz (Ty )= −Ty a. |
(4.9) |
Сила RBy лежит в плоскости хy, перпендикулярной к оси z. Из точки А пересечения этой плоскости с осью z опускаем перпендикуляр АВ = а + b на линию дей-
29
ствия RBy. Момент отрицателен, ибо с конца оси z к ее началу видно, что сила RBy стремится повернуть тело вокруг точки А по ходу часовой стрелки. Итак,
mz (RBy )= RBy (a +b). |
(4.10) |
Приняв во внимание формулы (4.9) и (4.10), запишем уравнение моментов силотносительно оси z:
∑mz (Fk )= −Ty a − RBy (a +b)= 0. |
(4.11) |
Итак, уравнения равновесия вала с закрепленной на нем шестерней имеют
вид
∑Fkx =Tx + RAx =0,
∑Fky =Ty + RAy + RBy =0,
∑Fkz =Tz + RAz + RBz =0,
∑mx (Fk ) = −mâð +Òy r =0,
∑my (Fk ) = −Tx r +Tz a + RBz (a +b) =0,
∑mz (Fk ) = −Ty a − RBy (a +b) =0.
Теперь переходим к решению этой системы шести уравнений с шестью неиз-
вестными (RAx, RAy, RAz, RBy, RBz и mвр). Из уравнения (4.6) имеем mвр = Ту r. Из уравнения (4.8) получим
RBz = Tx r −Tz a . a +b
Из уравнения (4.11) находим
RBy = −Tay+ba .
Теперь, подставив значение RBy в уравнение (4.2), а RBz в (4.3), соответственно, имеем
RÀy |
= − |
Ty b |
, RAz = − |
T |
x |
r +T |
z |
b |
. |
a +b |
|
|
a +b |
|
|
||||
|
|
|
|
|
|
|
|
Наконец, из (4.1) следует RAx = – Тх.
Значения RAx, RAy, RAz и RBy оказались отрицательными. Это означает, что направления сил RAx, RAy, RAz и RBy противоположны тем, которые предположительно были нами указаны на рисунке. Знак RBz может быть выяснен только после подстановки числовых значений Тх, Tz, a и r.
4.2. Определение реакций опор твердого тела при произвольной системе сил (задание С 5 [8])
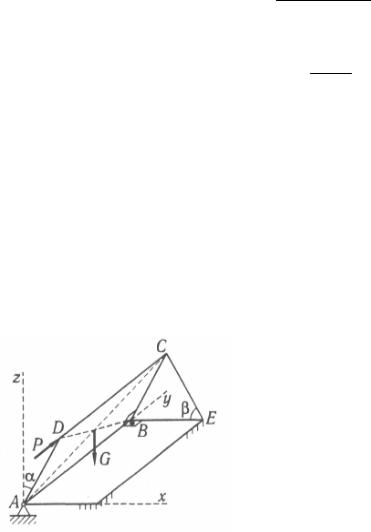
Дано: рама ABCD весом G = 1 кН, Р = 2 кН, сила Р параллельна оси Ау,
AD = BC = 60 cм, AB = CD = 100 см, α = 30°, β = 60° (рис. 4.2).
30
Рис. 4.2
