осн. киб лекц

а) линейные системы; б) нелинейные системы.

2В зависимости от коэффициентов уравнений и вида уравнений как линейные, так и нелинейные системы подразделяются на:

а) системы, описываемые обыкновенными дифференциальными уравнениями с постоянными коэффициентами;

б) системы, описываемые обыкновенными дифференциальными уравнениями с переменными коэффициентами;

в) системы, описываемые уравнениями в частных производных; г) системы с запаздыванием, описываемые уравнениями с запаздывающим аргументом.

3По характеру представления сигналов различают:

а) непрерывные системы; б) дискретные системы, среди которых выделяют импульсные, релейные, цифровые.

4 По характеру процессов управления:

а) детерминированные системы – системы с определенными переменными и процессами; б) стохастические системы – системы со случайными переменными и процессами.

5 По характеру функционирования.

В зависимости от того, по какому закону изменяется заданное значение регулируемой величины, системы автоматического управления подразделяются на:

а) системы стабилизации, поддерживающие постоянство регулируемой величины, т.е. yзад(t) = const;

б) системы программного регулирования, в которых заданное значение регулируемой величины изменяется по определенной заранее временной программе;

в) следящие системы, в которых заданное значение регулируемой величины изменяется в соответствии с состоянием некоторого заданного вектора переменных во времени;

г) системы оптимального управления, в которых показатель эффективности зависит не только от текущих значений координат, как в экстремальном регулировании, но также от характера их изменения в прошлом, настоящем и будущем, и выражается некоторым функционалом. Нахождение оптимального управления предполагает решение достаточно сложной математической задачи соответствующими методами, кроме того органической составной частью системы является компьютер;

д) адаптивные системы, в которых автоматически изменяются значения yзад , собственные параметры или структура при непредвиденных изменениях внешних условий на основании анализа состояния или поведения системы так, чтобы сохранялось заданное качество ее работы. Системы с изменением заданного значения регулируемой величины называют экстремальными, с изменением параметров – самонастраивающимися, с изменением структуры – самоорганизующимися.

1.6Тренировочные задания

1На рис. 1.12 изображен объект с входными и выходными сигналами.

АЧто такое объектуправления? Приведите конкретный пример.

В Какие внешние переменные являются управляющими?

С Какая переменная является управляемой переменной?

2 На рис. 1.13 изображена структурная схема системы автоматического регулирования.

А Какие принципы регулирования реализованы в АСР, изображенной на рис. 1.13? В Что значит регулирование по отклонению?

С Какая система регулирования является наиболее эффективной?

3 На какие основные классы делятся системы автоматического регулирования?

А К какому классу относится линейная система?

В На какие подклассы делится класс "характер функционирования"? С Что представляет собой класс "характер подачи сигналов"?

1.7 Тест

1 Какой процесс называется механизацией?

А Совокупность операций управления.

В Замена труда человека в рабочих операциях работой машин и механизмов. С Замена труда человека в операциях управления.

2 Систему управления образуют:

А Совокупность средств управления и объекта. В Совокупность средств управления.

С Объект управления.

3 Чем характеризуется любой элемент системы?

А Входной координатой. В Выходной координатой.

С Входной и выходной координатами.

4 Какой принцип регулирования был реализован в первом промышленном регуляторе уровня в котле паровой машины, изобретенном И. Ползуновым.

А Регулирование "по отклонению". В Регулирование "по возмущению". С Комбинированное регулирование.

5 Какая система регулирования называется автоматической?

А Все рабочие операции и операции управления выполняют автоматические устройства.

ВЧасть операций управления выполняют автоматические устройства, другую часть выполняет человек.

С Рабочие операции выполняют машины и механизмы, а операции управления – человек. 6 Детерминированные системы управления отражают:

А Характер подачи сигналов.

В Характер процесса управления. С Характер функционирования.

7 При классификации систем управления по характеру функционирования система автоматического регулирования может быть:

А Системой программного регулирования. В Системой с распределенными параметрами. С Стохастической системой.

8 Система автоматической стабилизации – это система, в которой поддерживается:

А yзад(t) = const. В yзад(t) = f (t). С yзад = f (x).

9 По основным видам уравнений динамики процессов управления системы подразделяются на:

А Непрерывные и дискретные.

В Детерминированные и стохастические. С Линейные и нелинейные.

10 В оптимальных системах управления показатель эффективности зависит от:

А Текущих значений координат.

ВТекущих значений координат, а также характера их изменения в прошлом, настоящем и будущем.

С Собственных параметров системы или структуры.

2РЕГУЛЯРНЫЕ СИГНАЛЫ И ИХ ХАРАКТЕРИСТИКИ

Втеории автоматического управления при рассмотрении тех или иных систем имеют место различные воздействия и сигналы. Анализ и синтез конкретных автоматических систем существенно упрощается, если пользоваться разработанной типизацией этих воздействий и сигналов. Математическим представлением сигналов является некоторая функция времени, определяющая закон его изменения, заложенный в нем независимо от физической природы. В зависимости от характера изменения сигнала во времени, формы математического представления различают регулярные – детерминированные и нерегулярные – случайные сигналы.

2.1 Определение регулярного сигнала

Сигнал называется регулярным, если его математическим представлением является заранее заданная функция времени, т.е. он описывается конкретной функцией времени. Реальный же сигнал рассматривается как случайный процесс, определяемый вероятностными характеристиками, так как нельзя заранее предвидеть его изменение во времени.

Выражение регулярного сигнала, определенного функцией времени, называют временным представлением сигнала. Форма записи этих функций различна. Одной из форм записи является представление в виде тригонометрического ряда, каждый член которого является простейшей гармонической функцией времени – косинус или синус. Эти функции получили название гармоник, каждая из которых характеризуется амплитудой, частотой и фазой. Множество амплитуд, частот и фаз называют спектром рассматриваемой функции времени. Подобное представление сигнала называется частотным. Временное и частотное представления сигнала совершенно адекватны. Выбор того или иного представления зависит от особенностей и постановки рассматриваемой задачи.

2.2 Основные типы регулярных сигналов. Периодические и непрерывные сигналы

К основным типам регулярных сигналов относятся периодический, почти периодический и непериодический сигналы.

Периодический сигнал представляет собой функцию времени, удовлетворяющую условию

где t – любой момент времени на интервале −∞ < t < ∞ ; T – некоторая постоянная – наименьший конечный промежуток времени, удовлетворяющий условию (2.1), называется периодом функции f(t).

Периодическая функция f(t) должна быть известна только в пределах промежутка времени, равного периоду Т, далее она в точности повторяется на протяжении каждого периода.

Периодический сигнал физически неосуществим, так как реальный сигнал не может продолжаться бесконечно, он имеет начало и конец. Однако в теоретических исследованиях понятие периодического сигнала используется широко и дает результаты, соответствующие наблюдаемым в действительности.

Периодическая функция произвольного вида, удовлетворяющая условиям Дирихле: ограниченная кусочно-непрерывная, имеет конечное число экстремумов на периоде, может быть представлена рядом

где А0 – постоянная составляющая; Аn – амплитуда; ωn = n ω – частота; ϕn – начальная фаза n-й гармоники.

Таким образом, периодический сигнал можно рассматривать как результат наложения друг на друга бесконечного количества гармоник и постоянной составляющей.

Почти периодический сигнал представляет собой функцию, состоящую из суммы гармонических составляющих с произвольными частотами. При управлении тем или иным процессом встречаются сигналы, частоты которых не находятся в простых кратных соотношениях, что и предопределяет использование почти периодических сигналов. Основным свойством последних является тот факт, что для них может быть определен приближенный период (почти период).

Непериодическим сигналом называется регулярный сигнал, определяемый непериодической функцией, заданной в пределах конечного (t1 ≤ t ≤ t2 ) или полубесконечного (t1 ≤ t < ∞) промежутка времени,

вне

КОТОРОГО ОНА ТОЖДЕСТВЕННО РАВНА НУЛЮ. ФОРМА СИГНАЛА МОЖЕТ БЫТЬ ПРАКТИЧЕСКИ ЛЮБОЙ.

Непериодический сигнал можно представить периодической фун-кцией времени с бесконечно большим периодом (рис. 2.2).

Математический метод представления сложных сигналов как периодических, так и непериодических в виде совокупности элементарных гармонических составляющих называется гармоническим анализом.

2.3 Преобразование Фурье, его основные свойства

Для характеристики спектров сигналов используется преобразование Фурье. Прямым преобразованием Фурье называется оператор

−∞

Преобразование Фурье ставит во взаимное соответствие два множества функций ( f (t) ↔ F(iω)) : первое

множество f(t) – функции действительного аргумента t; второе множество F(iω) – функции мнимого аргумента iω. Прямое преобразование Фурье (2.3) позволяет по заданному оригиналу f(t) найти его изображение F(iω), обратное преобразование (2.4) позволяет, наоборот, по заданному изображению F(iω) найти оригинал f(t).

Основными свойствами преобразования Фурье являются: 1 Свойство линейности.

i=1

где f(t), f1(t), ..., fn(t) – некоторые функции; F(iω), F1(iω), ..., Fn(iω) – изображения соответствующих функций.

4 Различный характер функции f(t).

Если функция f(t) четная, то ее изображение является вещественной функцией, четной относительно ω и определяется как

Если функция f(t) нечетная, то ее изображение является чисто мнимой функцией, нечетной относительно ω:

Общее количество свойств преобразования Фурье гораздо больше, но именно приведенные выше (2.5) – (2.9) используются при исследовании регулярных сигналов.

2.4 Спектры сигналов

Как уже было сказано, периодический сигнал представляется рядом Фурье (2.2), и структура его спектра полностью определяется амплитудами и фазами гармоник, т.е. модулем Аn и аргументом ϕn, n = 1, 2, …

Спектр амплитуд периодического сигнала, состоящий из равноотстоящих линий, длина которых пропорциональна амплитудам Аn соответствующих гармоник, приведен на рис. 2.3.

Непрерывная кривая, соединяющая концы спектра, называется огибающей спектра амплитуд. На практике часто удобна для применения комплексная форма ряда Фурье:

T → ∞ получают непериодическую функцию, спектр которой становится сплошным, но при этом амплитуды уменьшаются.

3С уменьшением длительности импульсов τ при постоянном периоде амплитуды гармоник уменьшаются, а спектр становится "гуще".

4Если с уменьшением длительности прямоугольных импульсов увеличивать амплитуду по закону

A0 = T1 , то их последовательность будет стремиться к последовательности дельта-функций, а амплитуд-

ный спектр – к постоянному для всех частот значению A = T1 .

Для непериодических сигналов вводится понятие спектральной плотности, которая представляет собой

Величину F(iω) называют также спектральной характеристикой непериодической функции, а модуль F(iω) = F(ω) – спектром.

Поскольку спектральная характеристика комплексная величина, то ее можно представить в виде

F(iω) = a(ω) +ib(ω) = F(ω)e−iϕ(ω) ,

∞∞

Структура спектра периодического сигнала полностью определяется модулем и фазой спектральной характеристики.

Зависимость модуля и фазы спектральной характеристики непериодического сигнала называют соответственно спектром амплитуд и спектром фаз непериодического сигнала. Особенности спектральных свойств непериодического сигнала состоят в следующем:

1Спектр всегда непрерывен и характеризуется плотностью амплитуд гармоник, приходящихся на интервал [0; ω].

2При уменьшении длительности импульса его спектр расширяется вдоль оси ω, а значения плотности амплитуд уменьшаются.

3Если одновременно с уменьшением длительности τ прямоугольного импульса увеличивать его

амплитуду по закону An = T1 , то импульс стремится к дельта-функции, а спектральная плотность к постоянной величине, равной единице во всем диапазоне частот (−∞;∞) .

2.5Распределение энергии в спектрах сигналов

Вслучае периодического сигнала речь ведут о распределении мощности в его спектре, которая определяется как

где А0, Аn – коэффициенты ряда Фурье соответствующего периодического сигнала; R – сопротивление элемента или участка, через который проходит сигнал.

Распределение энергии в спектре периодического сигнала представляется в виде суммы бесконечно малых слагаемых, соответствующих бесконечно малым участкам частотного спектра:

∞

W = 1 ∫[F(ω)]2 dω . (2.15)

π 0

Выражение 1π[F(ω)]2 dω представляет собой энергию, выделяемую спектральными составляющими

сигнала, расположенными в полосе частот dω в окрестности частоты ω, и называется энергетической спектральной плотностью непериодического сигнала. Формула (2.15) называется формулой Рейли или равенством Парсеваля и используется для выбора максимальной частоты пропускания при условии, что основные составляющие спектра пропускаются без изменения.

2.6 Практическая ширина спектра и искажения сигналов

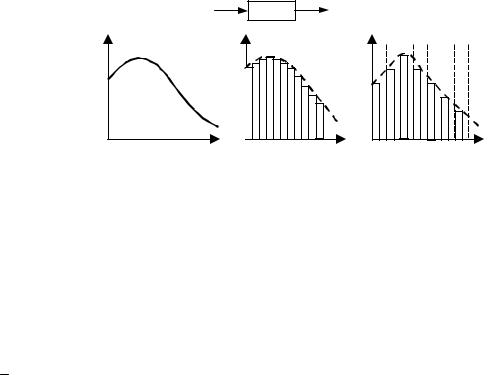
При передаче периодических сигналов через реальные системы управления может быть передано лишь определенное количество гармоник из их бесконечного числа. При этом важно передать гармонические составляющие с относительно большими амплитудами. В связи с этим вводится понятие практической ширины спектра сигнала, под которой понимается область частот, в пределах которой лежат гармонические составляющие сигнала с амплитудами, превышающими наперед заданную величину. При выборе практической ширины спектра сигнала необходимо учитывать требования к сигналу с энергетической точки зрения и с точки зрения сохранения его формы.

В случае непериодического сигнала так же, как и в случае периодического сигнала, желательно передавать составляющие сигнала со значительными амплитудами. С энергетической точки зрения практическая ширина спектра оценивается по области частот, в пределах которой сосредоточена подавляющая часть всей энергии сигнала, с точки же зрения допустимых искажений формы сигнала определить практическую ширину спектра не представляется возможным. Представление о характере искажений сигнала в зависимости от ширины спектра может быть получено при исследовании прохождения сигналов через системы с заданными характеристиками.

2.7 Представление сигналов

Сигналы могут быть представлены различным образом, при этом входной сигнал всегда является непрерывным, а представлению подлежит сигнал на выходе.

Один и тот же сигнал может иметь различную физическую природу – электрическую, звуковую, световую и т.д.

В теории управления наибольшее распространение получило математическое представление сигналов. Все виды математических представлений сигналов делятся на три основные группы:

1)непрерывное представление – выходной сигнал определен в любой момент времени (рис. 2.4, б);

2)дискретно-непрерывное представление – выходной сигнал является квантованным по времени и

непрерывно изменяется только по уровню (рис. 2.4, в); 3) дискретное представление – выходной сигнал квантован как по времени, так и по уровню (рис.

2.4, г).

Рис. 2.4 Виды математических представлений сигналов:

а– блок-схема системы; б – непрерывное; в – дискретно-непрерывное;

г– дискретное

Врезультате квантования сигнала по времени при дискретно-непрерывном и дискретном представлениях может произойти потеря информации, так как остаются значения сигнала только в дискретные моменты времени. Однако благодаря одному из свойств реальных систем в них при определенных условиях сохраняется полная информация о сигнале, если последний известен лишь в дискретные моменты времени. Это свойство известно как теорема Котельникова: сигнал, описываемый функцией с ограниченным спектром, полностью определяется своими значениями, отсчитанными через интервал вре-

мени ∆t = 12 Fс , где Fc – ширина спектра сигнала.

Смысл теоремы Котельникова состоит в том, что, если требуется передавать сигнал, описываемый функцией f (t) с ограниченным спектром, то достаточно передавать отдельные мгновенные значения, отсчи-

танные через конечный промежуток времени ∆t = 12 Fс . По этим значениям непрерывный сигнал может быть

полностьювосстановлен на выходе системы.

Математические представления сигналов на практике чаще всего реализуются в виде модуляции. Под модуляцией понимают изменение одного из параметров какого-либо физического процесса по закону представляемого сообщения. Так, в системах с электрическими сигналами под модуляцией понимают изменение одного из параметров высокочастотного электрического сигнала по закону передаваемого низкочастотного сообщения. В случае модуляции гармонического сигнала различают два основных вида модуляции: амплитудная модуляция и угловая модуляция, которая подразделяется на частотную и фазовую. На практике чаще всего встречаются смешанные виды модуляции – амплитуднофазовая или амплитудно-частотная, при этом один из видов модуляции является полезным, другой – паразитным.

2.8 Сигналы. Их виды

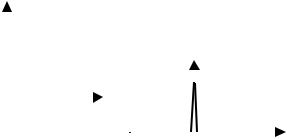
Наиболее часто в теории автоматического управления используются следующие сигналы. 1 Единичный скачок (рис. 2.5):

1(t) называется также функцией Хевисайда. Строго говоря, функция Хевисайда физически нереализуема, однако, если, к примеру, на исследуемом объекте резко открыть вентиль, в результате чего расход

Рис. 2.6 Единичный импульс

подаваемого вещества изменится скачком с F1 до F2 , то говорят, что на входе объекта реализован скачкообразный сигнал величиной F2 – F1 , и если последняя разность равна единице, то на входе реализуется единичный скачок.

Спектральная характеристика для единичного скачка:

2 Единичная импульсная функция – дельта-функция (рис. 2.6) – это функция, удовлетворяющая следующим условиям:

−∞

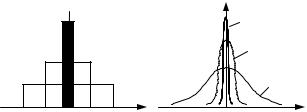
Дельта-функцию называют также функцией Дирака, она относится к классу сингулярных функций. Эту физически также нереализуемую функцию можно представить как импульс бесконечно малой длительности и бесконечно большой амплитуды, т.е. как предел, к которому стремится прямоугольный импульс с основанием ∆t и площадью, равной единице (рис. 2.7, а), если ∆t → 0 так, чтобы площадь импульса сохранялась равной единице. Также δ-функцию можно представить как предел некоторой функ-

ции (рис. 2.7, б):