Lysenko_physics_lek_2[1]
.pdf
інтегрування за усією довжиною провідника.
Як випливає із закону Ампера (1.1), сила dF перпендикулярна як до напряму проходження
електричного струму Idl , так і до вектора B , а її величина пропорційна синусу кута між цими
векторами |
(як відомо, |
| [dl ´ B] |=| dl | × | B | ´ |
||
r^ r |
|
Idl |
й B |
паралельні, |
´sin(dl , B) ). Коли вектори |
||||
сила dF |
дорівнює нулю. |
Для |
визначення |
|
|
Напрям струму |
|
|
I |
S |
|
|
|
Напрям |
N |
|
індукції |
dF |
|
магнітного |
|
|
поля |
r |
Напрям сили |
|
B |
|
напрямку сили |
dF |
зручно використовувати |
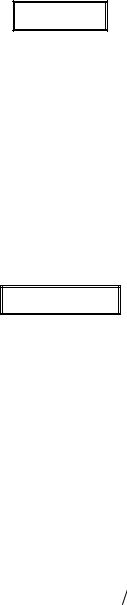
Рисунок 1.6 – До правила лівої руки |
|
правило лівої руки (рис. 1.6): якщо ліву долоню |
||||
|
||||
розмістити так, |
щоб |
витягнуті пальці показували напрям струму I , а лінії індукції |
||
магнітного поля B входили в долоню, то відхилений великий палець покаже напрям сили dF , що діє на провідник.
Як зазначалось вище, коефіцієнт пропорційності k у формулі (1.1) залежить тільки
від вибору одиниць величин dl , B , I і dF . У системі СІ цей коефіцієнт дорівнює одиниці k =1, індукція магнітного поля виміряється в теслах (Тл) .
7 Закон Ампера дозволяє визначити числове значення магнітної індукції B .
Припустимо, що елемент провідника dl зі струмом I є перпендикулярним до напряму магнітного поля (sin(dl , B) =1). У цьому випадку сила, що діє на елемент провідника зі струмом, буде максимальною, тобто
dF = IBdl ×sin(dl , B) = IBdl = dFmax .
Експериментально визначивши значення максимальної сили dFmax , що діє на елемент провідника dl зі струмом I , можемо знайти модуль вектора індукції магнітного поля
B = |
1 |
dFmax |
. |
(1.2) |
|
||||
|
I dl |
|
||
З формули (1.2) випливає, що магнітна індукція B чисельно дорівнює силі, що діє з боку поля на одиницю довжини провідника, по якому проходить електричний струм
одиничної сили і який розміщений перпендикулярно до напряму магнітного поля B . Таким чином, магнітна індукція є силовою характеристикою магнітного поля. Напрям вектора
індукції магнітного поля B , як говорилося вище, визначається напрямом від південного полюса S до північного N магнітної стрілки, що вільно встановилась у магнітному полі
(див. рис. 1.2).
З формули (1.2) також неважко з’ясувати зв’язок між одиницею виміру індукції магнітного поля та іншими одиницями виміру в системі СІ: 1 Тл=1 Н/(А∙м) .
8 Дослід свідчить, що для магнітного поля, як і для електричного, виконується
принцип суперпозиції: поле B , яке створюється декількома струмами, дорівнює векторній
сумі полів Bi , що створюються кожним струмом окремо |
|
B = åBi . |
(1.3) |
§ 2 Сила Лоренца [5]
1 Сила Ампера, що діє на провідник довжиною dl зі струмом I в магнітному полі з індукцією B ,
dF = I[dl ´ B] |
(2.1) |
11
обумовлена тим, що магнітне поле діє на рухомі носії електричного струму. Від носіїв струму дія сили передається провіднику, по якому вони переміщуються. Знайдемо силу Fm з
боку магнітного поля, що діє на окремо взятий рухомий електричний заряд.
Для цього подамо силу струму I у вигляді
I = jS = nqυS ,
де j – густина електричного струму; S – площа поперечного перерізу провідника; n , q та
υ відповідно концентрація, заряд та швидкість носіїв електричного струму. Підставлення цього виразу в (2.1) дає
r
dF = nqυS[dl × B] = nqSdl[υ× B] .
Тут використали, що напрями векторів dl та υ збігаються. Добуток nSdl дорівнює числу носіїв струму, що знаходяться на ділянці провідника dl . Розділивши dF на це число, знайдемо силу Fm , що діє на заряд q , який рухається зі швидкістю υ, з боку магнітного поля
r |
(2.2) |
Fm = q[υ× B] . |
Ця формула визначає силу (будемо називати її магнітною), що діє в точці поля, де магнітна індукція дорівнює B , на точковий заряд q , який рухається зі швидкістю υ. Модуль магнітної сили дорівнює
Fm = qυB sin α , |
(2.3) |
де α – кут між векторами υ й B . З (2.3) випливає, що на заряд, який рухається вздовж ліній поля, не діє магнітна сила (у цьому випадку α = 0 ).
Магнітна сила завжди спрямована перпендикулярно до швидкості зарядженої частинки, як це випливає з (2.3). Тому вона роботи над частинкою не виконує. Отже, за допомогою магнітного поля енергію частинки змінити не можна.
У випадку, коли заряджена частинка знаходиться як в електричному, так і в магнітному полі, сила, що діє на заряджену частинку з боку електромагнітного поля, дорівнює
r |
(2.4) |
F = qE + q[υ× B] . |
Цей вираз отримав Лоренц шляхом узагальнення експериментальних даних, і його називають
силою Лоренца.
§ 3 Рух зарядженої частинки в однорідному магнітному полі [9]
Нижче подано два варіанти викладення цього питання. У першому варіанті використовуються більше фізичні ідеї. Другий варіант базується на точному математичному розв’язанні вихідних рівнянь. Бажано ознайомитися з обома підходами. Для підготовки до практичного заняття, модульного контролю, іспиту можна використати будь-який варіант за вашим вибором.
Перший варіант
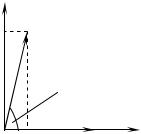
Розглянемо рух зарядженої частинки в однорідному магнітному полі, початкова швидкість якої спрямована під кутом α до вектора індукції магнітного поля (див. рис. 3.1).
r |
та формулу для магнітної |
Для цього використаємо другий закон Ньютона m dυ dt = åFi |
|
складової сили Лоренца |
|
r |
(3а.1) |
Fm = q[υ× B] . |
|
12 |
|
Виходячи з формули для магнітної складової сили Лоренца (3а.1), неважко з’ясувати, що ця сила завжди спрямована перпендикулярно до вектора швидкості частинки (згадайте властивості векторного добутку). Це означає, що робота магнітної складової сили Лоренца завжди дорівнює нулю:
r r |
r r |
r ^ r |
×dt =0. |
A = òFm ×dr |
= òFm ×udt =òFmucos(Fm , u)dt =òFmu×0 |
||
Таким чином, магнітна складова сили Лоренца не змінює кінетичну енергію частинки, а отже, не змінює і модуль її швидкості. Вона тільки викривлює траєкторію.
Запишемо другий закон Ньютона з урахуванням X магнітної складової сили Лоренца (3.1) і отримаємо
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u0x |
r |
|
|
|
|
|
|
|
|
du |
|
|
|
r |
|
|
r |
|
|
|
|
|
|
|
|
|
u0 |
|
|||||
|
|
|
|
|
m |
= q[u´ B]. |
|
|
|
(3а.2) |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
У цьому співвідношенні m, q – маса та заряд частинки, υ |
– її |
|
|
α |
|
||||||||||||||||||||||||
швидкість, B – індукція магнітного поля. Спрямуємо вісь |
Z |
|
|
|
|||||||||||||||||||||||||
|
|
Z |
B |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
O |
|||
вздовж |
вектора B |
|
(див. |
рис. 3.1). |
Тоді |
|
B = Bez . |
Подамо |
|
|
|||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||
вектор |
швидкості у |
вигляді |
|
суми |
двох |
|
|
|
|
|
r |
|
|
u0z |
|
||||||||||||||
r |
|
складових: uzez , |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
, перпендикулярної до осі Z : |
|
|
Рисунок 3.1 |
|
||||||||||||||
спрямованої вздовж осі Z , та u |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
r |
r |
|
|
|
|
|
(3а.3) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u = uzez + u . |
|
|
|
|
|
||||||||
Підставимо (3а.3) в (3а.2) і отримаємо |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
d(u |
e |
z |
+ u |
|
) |
|
|
|
|
r |
r |
r |
|
|
|
|
|||
|
|
|
|
|
|
|
m |
|
|
z |
|
|
|
|
|
= q[(uzez + u )´ Bez ], |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
або |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
du |
z |
r |
|
|
du |
|
|
|
|
r |
|
|
|
|
r |
r |
r |
|
r |
|
r |
|
|||||
|
m |
|
|
ez |
+ |
|
|
|
|
= q[uzez |
´ Bez ]+ q[u |
´ Bez |
]= 0 + q[u |
´ B]. |
|
||||||||||||||
|
|
dt |
|
|
|
dt |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Запишемо паралельну та перпендикулярну до осі Z компоненти отриманого рівняння: |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
du |
|
r |
r |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
= q[u ´ B], |
|
|
|
|
(3а.4) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
d(uzez ) |
|
= 0. |
|
|
|
|
|
(3а.5) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
Таким чином, система незалежних рівнянь (3а.4) та (3а.5) описує зміну швидкості частинки в магнітному полі з часом.
З рівняння (3а.5) та рис. 3а.1. випливає, що
uz = u0 z º u0 cosa = const . |
(3а.6) |
Тобто вздовж осі Z частинка рухається рівномірно.
Розглянемо тепер детально рівняння (3а.4), яке описує рух частинки в площині, що
перпендикулярна до осі Z . Модуль швидкості частинки в магнітному полі не змінюється |
|
(див. коментар до формули (3а.1)), тобто він є сталим у часі і дорівнює (див. рис. 3а.1) |
|
u = u0 = u0 sin a . |
(3а.7) |
r |
|
Сила Fm = q[u ´ B] є також сталою за величиною, вона перпендикулярна до траєкторії |
|
r |
r |
частинки. Це означає, що і прискорення частинки aдоц = Fm / m = q[u ´ B]/ m буде
перпендикулярне до траєкторії руху, тобто нормальним, а також сталим за модулем. Відомо, що коли частинка рухається по колу, то її прискорення є доцентрове (нормальне) і стале за модулем, швидкість також є сталою за модулем. Звідси випливає, що частинка в поперечній
13
площині буде рухатись по колу. При цьому площина цього кола перпендикулярна до магнітного поля (осі Z ).
Підставляючи в (3а.4) формулу доцентрового прискорення
r |
|
u2 |
|
r |
r |
|
|
| aдоц |= |
|
|
|
=| q[u ´ B]/ m |=| qu B / m |, |
|||
|
R |
||||||
|
|
|
|
|
|
|
|
неважко знайти радіус R цього кола |
|
|
|
|
|
||
|
R = |
|
u |
= |
mu0 sin a |
, |
|
|
|
| qB / m | |
| q | B |
||||
циклічну частоту обертання (циклотронну частоту)
w = u / R =| q | B / m ,
період обертання
T = 2p = 2pm . w | q | B
(3а.8)
(3а.9)
(3а.10)
Аналізуючи формули (3а.9)-(3а.10), зазначимо, що період і частота обертання не залежать від швидкості частинки у нерелятивістському випадку. Використовуючи цю особливість, будують роботу прискорювача заряджених частинок, який називають
циклотроном.
B |
|
|
|
υ |
|
q |
= + q |
B |
|
|
Fm |
q = - q |
||
|
υ |
|
Fm |
|
|
|
|
|
Рисунок 3.2 Визначивши напрям магнітної сили, а отже, і доцентрового прискорення, знайдемо
напрям обертання частинки по колу (див. рис. 3.2, тут магнітне поле спрямоване до читача). Якщо заряд q = + | q | є додатним, то напрями вектора B та кутової швидкості ω протилежні. Коли заряд q = − | q | є від’ємним, то ці напрями збігаються.
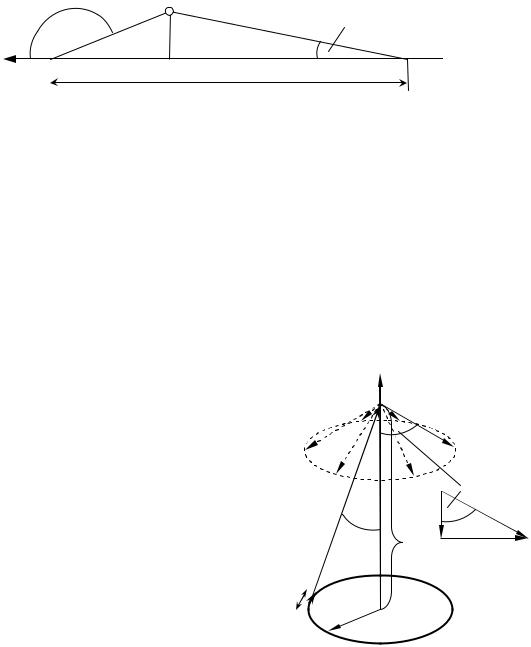
Таким чином, частинка в поперечній площині до магнітного поля рухається рівномірно по колу, а вздовж магнітного поля рухається зі сталою швидкістю. Результуючий рух є рухом частинки по спіралі, вісь якої паралельна магнітному полю (див. рис. 3.3).
Визначимо крок спіралі як відстань, яку частинка проходить вздовж осі Z за період обертання T = 2p
w (див. рис. 3.3):
h = T ×uz = |
2p |
u0z = |
2pm |
u0 cosa . |
(3а.11) |
|
|
||||
|
w |
qB |
|
||
r
X u0
|
O |
α |
Z |
|
|
||
|
|
|
|
Y |
|
|
R |
|
|
|
h |
|
|
|
Рисунок 3.3 |
|
|
|
14 |
Таким чином, в однорідному магнітному полі заряджена частинка в загальному випадку рухається вздовж спіралі. Радіус та крок спіралі визначаються за формулами (3а.8) та (3а.11). Кутова частота обертання (кутова швидкість) подається співвідношенням (3а.9), період обертання – (3а.10).
Другий варіант
Розглянемо рух зарядженої частинки в однорідному магнітному полі, початкова швидкість якої спрямована під кутом α (див. рис. 3.1) до вектора індукції магнітного поля.
Для цього використаємо другий закон Ньютона |
r |
|
|||||||||||
m du dt = åFi та формулу для магнітної |
|||||||||||||
r |
і отримаємо |
|
|
||||||||||
складової сили Лоренца Fm = [u´ B] |
|
|
|||||||||||
|
|
|
du |
|
|
|
r |
r |
|
||||
|
|
m |
= q[u´ B]. |
(3б.1) |
|||||||||
|
|
|
|
|
|||||||||
|
|
|
dt |
|
|
|
|
|
|
|
|
||
У цьому співвідношенні m, q – маса та |
заряд |
частинки, |
υ – її швидкість, B – індукція |
||||||||||
магнітного поля. Спрямуємо вісь Z |
|
|
|
|
|
|
|
|
|
|
|
|
r |
вздовж вектора B . Тоді B = Bez . Запишемо рівняння |
|||||||||||||
(3б.1) у проекціях на осі X ,Y , Z : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dux |
|
= |
q |
uy B, |
|
||||||
|
|
dt |
|
|
|
||||||||
|
|
|
|
m |
|
|
|
|
|
||||
|
|
duy |
= - |
|
q |
|
ux B, |
(3б.2) |
|||||
|
|
dt |
m |
||||||||||
|
|
|
|
|
|
|
|||||||
|
|
duz |
|
= 0. |
|
|
|
|
|
||||
|
|
dt |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||||
З останнього рівняння системи (3б.2) випливає, що uz |
є константою, тобто |
||||||||||||
|
uz = u0z = u0 cosa |
|
|||||||||||
Тут враховано, що початкова швидкість частинки спрямована під кутом α до осі Z (див.
рис. 3.1).
Якщо продиференціювати перше рівняння системи (3б.2) та в отриманий результат підставити друге рівняння системи (3б.2), то знайдемо
|
d 2u |
x |
æ qB |
ö2 |
|
|
|
= -ç |
÷ ux , |
|
|
|
dt2 |
|
|
||
|
|
è m |
ø |
|
|
або |
|
|
|
|
|
|
d 2ux |
2 |
|
|
|
|
|
|
+ w ux = 0. |
(3б.3) |
|
|
dt2 |
|
|||
|
|
|
|
|
|
У рівнянні позначено |
|
|
|
|
|
|
|
w = qB . |
|
(3б.4) |
|
|
|
|
m |
|
|
Цю величину називають циклотронною частотою. Рівняння (3б.3) в математиці називають
диференціальним рівнянням гармонічних коливань. Його розв’язок є
ux = Acos(wt + j0 ) , |
(3б.5) |
де A, j0 – сталі, які визначаються початковими умовами. Для того щоб впевнитись, що
(3б.5) є розв’язком (3б.3), достатньо підставити (3б.5) в (3б.3). Далі з першого рівняння (3б.2) знаходимо
15
uy = |
dux |
1 |
= -Asin(wt + j0 ) . |
(3б.6) |
|||
dt |
|
æ q |
ö |
||||
|
|
ç |
|
B÷ |
|
|
|
|
|
|
|
|
|||
|
|
|
è m |
ø |
|
|
|
З’ясуємо сутність констант A та j0 . В початковий момент часу t = 0 проекції швидкості ux і uy мають значення u0x , u0 y . Підставляємо їх у (3б.5) та (3б.6) і отримуємо
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u0x = Acosj0 , u0 y = -Asin j0 . Звідси знаходимо, що u02x + u02 y = A cos2 j0 + sin 2 j0 |
= A . |
|||||||||||||
|
|
|
|
|||||||||||
Зрозуміло, що |
|
u02x + u02 y = u0 – модуль складової початкової швидкості частинки, |
||||||||||||
яка перпендикулярна |
до |
осі |
Z . Таким чином, |
A = u0 . |
Виберемо |
вісь |
X так, |
щоб в |
||||||
початковий момент |
часу |
|
|
r |
лежала в |
площині |
XZ . |
Тоді з |
рис. 3.1 |
|||||
t = 0 швидкість u0 |
||||||||||||||
знаходимо, що |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u0x = u0 sin a , |
u0 y = 0 . |
|
|
|
|
|
|
|
|
Це означає, що j0 = 0, |
u0 = u0 sin a . З урахуванням вищесказаного, рівняння (3б.5) |
|||||||||||||
та (3б.6) набирають вигляду |
|
|
|
|
|
|
|
|
|
|
|
|||
ux = u0 cos(wt), |
(3б.7) |
|
uy = -u0 sin(wt), |
||
|
де u0 = u0 sin a .
Використаємо визначення швидкості і знайдемо залежність координат частинок від
часу:
ux = dx |
|
|
|
|
|
x |
t |
|
|
|
|
|
|
|
|
= u0 cos(wt) Þ òdx = òu0 cos(wt)dt Þ |
|
|
|
|
|
|
|||||||||
dt |
|
|
|
|
|
x0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
x = x + |
u0 |
sin(wt) , |
|
|
|
|
|
|
(3б.8) |
||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
0 |
|
w |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
uy = dy |
|
|
|
|
|
y |
t |
|
|
|
|
|
|
|
|
= u0 sin(wt) Þ òdy = ò- u0 sin(wt)dt Þ |
|
|
|
|
|
|
|||||||||
dt |
|
|
|
|
y0 |
0 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
y = y0 + |
u0 |
(cos(wt) -1) , |
|
|
|
|
|
|
(3б.9) |
|||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
w |
|
|
|
|
|
|
|
|
|||
|
|
dz |
|
|
|
z |
t |
|
|
|
|
|
|
|
|
|
uz = |
= u0z Þ òdt = òu0z dt Þ |
|
|
|
|
|
|
|
||||||
|
dt |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
z0 |
0 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
z = z0 + u0z ×t . |
|
|
|
|
|
|
(3б.10) |
|||||
Початок координатних осей |
вибираємо |
так, щоб x |
= 0, y |
0 |
- |
u0 |
= 0, z |
0 |
= 0 . Це |
||||||
|
|||||||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
w |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
приводить до спрощення математичних співвідношень без зміни фізичної сутності. Тоді з
(3б.8)-(3б.10) отримуємо
x = |
|
u0 |
|
sin(wt), |
|
|
|
|
|||
|
|
w |
|
||
y = |
u0 |
cos(wt), |
(3б.11) |
||
|
|||||
|
|
w |
|
||
z = u0z ×t.
16
Порівнюючи перші два рівняння (3б.11) з (3б.1) та (3б.2), робимо висновок, що
частинка в площині XY рівномірно рухається по полу з радіусом |
|
|||||||||
|
|
|
|
R = u0 |
= u0 sin a . |
(3б.12) |
||||
|
|
|
|
|
w |
|
w |
|
||
Кутова частота обертання частинки по цьому колу визначається циклотронною |
||||||||||
частотою (3б.4) w = |
|
q |
|
B m . |
|
|
|
|
||
|
|
|
|
|
|
|||||
Виходячи з третього рівняння системи (3б.11), стверджуємо, що частинка рухається |
||||||||||
вздовж осі Z рівномірно. Суперпозиція рівномірного руху вздовж осі Z |
та рівномірного |
|||||||||
руху по колу в площині XY дасть рух частинки по спіралі (див. рис. 3.3). |
|
|||||||||
Визначимо крок спіралі як відстань, яку частинка проходить вздовж осі Z за період |
||||||||||
обертання T = 2p w (див. рис. 3.3): |
|
|
|
|
||||||
|
|
|
|
h = T ×uz = |
2p |
u0z = |
2pm |
u0 cosa . |
(3б.13) |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
w |
|
qB |
|
||
Таким чином в однорідному магнітному полі заряджена частинка в загальному випадку рухається по спіралі. Радіус та крок спіралі визначаються формулами (3б.12) та (3б.13). Кутова частота обертання (кутова швидкість) дається співвідношенням (3б.4),
період обертання дорівнює |
|
|
|
|
|
T = |
2p |
= |
2p×m |
. |
(3б.14) |
w |
|
||||
|
|
qB |
|
||
§ 4 Закон Біо-Савара-Лапласа. Індукція магнітного поля, яке створене відрізком із струмом. Індукція нескінченно довгого прямого провідника зі струмом. Індукція на осі колового струму [5]
1 Біо й Савар провели в 1820 р. дослідження магнітних полів, які створюються струмами, що проходять по тонких провідниках різної форми. Лаплас проаналізував експериментальні дані, отримані Біо й Саваром, і встановив залежність, яка отримала назву закону Біо-Савара-Лапласа.
Відповідно до закону Біо-Савара-Лапласа індукція
магнітного поля, яка створюється елементом струму Idl , визначається за формулою
r |
m |
|
|
r |
|
|
|
0 |
|
I[dl ´r ] |
|
|
|
||
dB = |
|
|
|
|
, |
(4.1) |
|
4p |
|
r3 |
|||||
|
|
|
|
|
|||
де dl – вектор, модуль якого дорівнює елементарній довжині ділянки зі струмом I і спрямований у той бік, куди проходить струм (рис. 4.1); r – вектор, що проведено
від елемента струму в ту точку, у якій визначається dB ; r – модуль цього вектора; m0 – так звана магнітна стала, що дорівнює
m0 = 4p×10−7 Тл∙м/А = 4p×10−7 Гн/м, |
(4.2) |
I
dB
|
r |
|
dl |
α |
|
|
|
|
Рисунок 4.1 – Індукція |
dB |
|
магнітного |
поля, |
що |
створюється |
елементом dl |
|
провідника, |
по |
якому |
проходить струм I
де Гн (генрі) – одиниця індуктивності (про цю одиницю детально мова буде йти далі).
Згідно з цим законом магнітне поле будь-якого струму може бути обчислене як векторна сума (суперпозиція) полів, які створюються окремими елементарними ділянками
струму Idl :
17
r |
r |
|
|
m |
|
|
|
|
r |
|
|
|
0 |
|
I[dl ´r ] |
|
|||||
B = òdB = |
ò |
|
|
|
|
|
. |
|||
4p |
|
r |
3 |
|
||||||
|
|
|
|
|
|
|
|
|||
Модуль вектора dB , виходячи з виразу (4.1), визначається співвідношенням |
||||||||||
|
dB = m0 |
|
I ×dl ×sin a |
, |
(4.3) |
|||||
|
|
|
||||||||
|
4p |
|
|
|
|
r2 |
|
|
|
|
де α – кут між векторами dl й r .
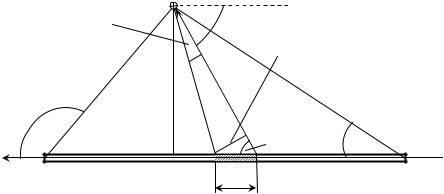
2 Застосуємо закон Біо-Савара-Лапласа для обчислення індукції магнітного поля, яке створене відрізком із струмом, наприклад в точціO (див. рис. 4.2), яка знаходиться на відстані a від осі відрізка. При цьому вважаємо кути між напрямами векторів, проведених з кінців відрізка зі струмом до точки O і напрямом електричного струму I , відомими і такими, що дорівнюють відповідно a1 й a2 (див. рис. 4.2).
|
dB O |
|
|
|
da |
|
α |
|
|
|
|
|
r × dα |
|
|
a |
r |
|
|
|
|
|
|
|
a2 |
P |
K |
M |
a1 |
|
α |
|||
I |
|
dl |
N |
|
Рисунок 4.2 – До |
обчислення індукції магнітного поля, що ство- |
|||
рюється відрізком провідника зі струмом |
|
|||
Розіб’ємо відрізок із струмом I на елементарні ділянки dl (див. рис. 4.2). Відповідно до закону Біо-Савара-Лапласа елемент зі струмом Idl створює магнітне поле з індукцією dB ,
що визначається формулою (4.1). Зауважимо, що вектори dB від усіх елементів струму I ×dl в точці O паралельні осі Z , яка перпендикулярна до площини рисунка (див. рис. 4.2). Тому
відповідно до принципу суперпозиції при визначенні індукції магнітного поля B у точці O можна перейти від геометричного до алгебраїчного підсумовування (інтегрування):
r |
ò |
r r |
ò |
r |
m |
× I |
|
ò |
sin a |
|
|
B = |
dB = ez × |
dB = ez × |
4p |
× |
r2 |
×dl , |
(4.4) |
||||
|
|
0 |
|
|
|
||||||
|
l |
|
l |
|
|
|
|
l |
|
|
|
де dB – модуль вектора dB (див. формулу (4.3)); α – кут між векторами dl й r . Проаналізуємо вираз (4.4). Зрозуміло, що під знаком інтеграла у співвідношенні (4.4)
кут α та довжина вектора r змінюються при переході від одного елемента довжини dl до іншого (див. рис. 4.2.). Тому перетворимо підінтегральний вираз так, щоб він залежав тільки від однієї змінної, наприклад кута α .
Неважко знайти зв’язок елемента dl з елементарним кутом da та довжиною вектора r . З трикутника DKMN (див. рис. 4.2) випливає, що dl ×sin a = KM , а з трикутника DOKN – KM = r ×da . Звідси маємо dl = r ×da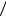
sin a . Далі з трикутника DOPN можемо виразити
довжину вектора r через відстань a та кут α : r = a / sin a . Тоді співвідношення (4.4) набуде вигляду
r |
r m0 × I |
α2 da r m0 × |
|||
B = ez × 4p |
× ò |
r |
= ez × |
4p× |
|
|
|
α1 |
|
|
|
|
|
|
|
18 |
|
I ×αò2sin a×da . a α1
Далі проведемо інтегрування і отримаємо шуканий вираз для індукції магнітного поля, що створюється відрізком провідника зі струмом:
B = |
m0 × I |
×(cosa - cosa |
2 |
) |
. |
(4.5) |
|
||||||
|
4p×a |
1 |
|
|||
|
|
|
|
|
|
3 Застосуємо закон Біо-Савара-Лапласа для обчислення індукції магнітного поля, яке створене нескінченно довгим прямим провідником зі струмом (див. рис. 4.3). Для цього використаємо формулу для індукції магнітного поля від відрізка із струмом (4.5).
|
|
|
B |
|
|
|
O |
|
|
|
a2 |
|
|
|
|
a1 |
|
I |
|
|
|
|
|
a |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
Рисунок |
|
4.3 – До |
обчислення індукції магнітного поля, що ство- |
|||||
|
||||||||
рюється нескінченним тонким провідником зі струмом
З рис. 4.3 випливає, що коли довжина відрізка b буде прямувати до нескінченності, то кут a1 буде прямувати до нуля, а кут a2 – до 180° . Це означає, що коли відрізок
перетвориться в нескінченно довгий провідник із струмом (b = ∞ ), кути будуть мати значення
a1 = 0, a2 =180° . |
(4.6) |
Тоді індукцію від нескінченно довгого тонкого провідника із струмом знайдемо, підставивши значення (4.6) в (4.5):
|
|
B = |
m0 × I |
×(1- (-1))= |
m0 × I |
, тобто |
|
B = |
m0 × I |
|
. |
|
|
|
(4.7) |
|||||||||||||
|
|
2p×a |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
4p×a |
|
|
|
|
2p×a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Таким чином, отримали співвідношення |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
(4.7), яке визначає індукцію магнітного поля від |
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
|||||||||||
нескінченного тонкого провідника із струмом I . |
|
|
|
|
|
|
|
|
|
|
|
|
|
O |
|
|
|
|||||||||||
Слід зазначити, що напрям вектора B |
можна |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
визначити за правилом правого гвинта: коли |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
гвинт встановити паралельно струму й |
|
|
|
|
|
|
|
|
|
|
|
|
|
dB |
|
|
|
|||||||||||
обертати його так, щоб поступальний рух |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
-b |
|
|||||||||||
гвинта був |
спрямований вздовж |
струму, |
то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
обертання |
шапочки |
гвинта буде |
визначати |
|
|
|
|
|
|
|
|
|
|
β |
r |
2 |
|
dB |
||||||||||
|
|
|
|
|
|
|
|
r |
|
|
||||||||||||||||||
напрям силових ліній індукції магнітного поля. |
|
|
|
|
|
|
|
|
|
|
dBxex |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
x |
|
|
|
|||||||||||
4 Застосуємо |
закон Біо-Савара-Лапласа |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dB |
|
|||||||||||
для обчислення індукції магнітного поля на осі |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
колового струму (див. рис. 4.4). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Розіб’ємо круговий виток, по |
якому |
|
dl |
|
|
I |
|
R |
|
|
|
|
|
|
|
|||||||||||||
проходить струм I , |
на елементи |
довжини |
dl |
|
|
|
|
|
|
|
|
|
|
|
|
O′ |
|
|
|
|||||||||
(див. рис. 4.4). Елемент довжини dl |
зі струмом I |
|
|
|
|
|
|
|
|
|
|
Рисунок 4.4 |
|
|
|
|||||||||||||
створює в точці O магнітне поле dB , яке |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
визначається законом Біо-Савара-Лапласа (4.1). Відповідно до цього закону вектор |
dB є |
|||||||||||||||||||||||||||
перпендикулярним до радіуса-вектора |
r й |
вектора |
dl (див. |
рис. 4.4), а його модуль |
||||||||||||||||||||||||
відповідно до (4.3) дорівнює |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
r |
m0 |
|
I ×dl |
×sin p |
= m0 |
|
|
I ×dl |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
| dB |= |
× |
× |
|
. |
|
|
|
|
|
|
(4.8) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
4p |
|
|
r2 |
2 |
4p |
|
|
|
r2 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
19 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Тут враховано, що кут α між векторами r |
й dl |
дорівнює π / 2. |
|
|
|
|||||||||||||||||||||||||||||
Подамо вектор dB у вигляді суми двох векторів: |
вектора Bxex , який спрямований |
|||||||||||||||||||||||||||||||||
паралельно осі X , та вектора dB , який перпендикулярний до осі X (див. рис. 4.4). |
|
|||||||||||||||||||||||||||||||||
Знайдемо векторну суму паралельних осі X |
компонент вектора dB . Виходячи з |
|||||||||||||||||||||||||||||||||
рисунка 4.4, неважко знайти проекцію |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
dBx = -dB ×cos(p/ 2 -b) = - m0 |
× |
I ×dl ×sin b |
. |
|
|
(4.9) |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
У цій формулі кут β – кут між віссю |
|
|
|
|
|
|
|
|
|
|
4p |
|
|
|
|
|
|
r2 |
|
|
|
|||||||||||||
|
X |
|
та вектором r . Зазначимо, що для всіх елементів |
|||||||||||||||||||||||||||||||
струму Idl кут β має одне і те саме значення (див. рис. 4.4) |
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
sin b = |
R |
= |
|
|
|
R |
|
. |
|
|
|
|
|
|
|
|
(4.10) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
R2 + x2 |
|
|
|
|
|
|
|
||||||||
Відповідно до принципу суперпозиції знаходимо результуючу проекцію Bx |
шляхом |
|||||||||||||||||||||||||||||||||
підсумовування усіх елементарних проекцій dBx |
(або, в нашому випадку, їх інтегруванням) |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
m0 |
|
|
|
I |
|
|
|
|
|
2πR |
|
|
|
|
|
I |
|
|
|
|
|
||||||
Bx = |
ò |
dBx = - |
× |
|
|
×sin b× |
ò |
dl = - |
m0 |
× |
×sin b×2pR = |
|
||||||||||||||||||||||
4p |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
r2 |
|
|
|
|
|
4p |
r2 |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
m0 |
|
|
I |
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
m0 × I × R2 |
|
|
|
|||||||
= - |
4p |
× |
|
|
|
× |
|
|
|
|
|
×2pR = - |
2(R2 + x2 )3/ 2 |
. |
(4.11) |
|||||||||||||||||||
(R2 + x2 ) |
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
R2 + x2 |
||||||||||||||||||||||||||||||||
Знайдемо векторну суму перпендикулярних до осі |
X компонент вектора dB ( dB ). |
|||||||||||||||||||||||||||||||||
Зазначимо – у цій сумі для кожного вектора |
dB можна знайти йому протилежний. Це |
|||||||||||||||||||||||||||||||||
означає, що сума усіх векторів dB буде дорівнювати нулю. |
|
|
|
|||||||||||||||||||||||||||||||
Таким чином, результуюча індукція магнітного |
поля B |
від колового |
витка зі |
|||||||||||||||||||||||||||||||
струмом буде визначатися співвідношенням |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
r |
|
|
|
r |
|
|
|
|
m0 × I × R2 |
|
|
|
|
r |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
B = Bxex |
= - |
2(R2 + x2 )3/ 2 |
ex |
. |
|
|
(4.12) |
|||||||||||||||||||||
§ 5 Взаємодія двох |
нескінченно |
довгих паралельних |
провідників. Ампер – |
|||||||||||||||||||||||||||||||
одиниця вимірювання сили струму [15] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
1 У 1820 р. Ампер експериментально встановив, що два прямі паралельні струми притягуються, а антипаралельні відштовхуються. Знайдемо силу взаємодії двох паралельних нескінченних струмів.
Розглянемо два нескінченно довгі паралельні провідники із струмами 1 і 2 (рис. 5.1). Індукція магнітного поля, що створюється нескінченно довгим провідником зі струмом I1 в точці A на відстані R від провідника 1, визначається співвідношенням
B = |
m0 I1 |
. |
(5.1) |
|
|||
1 |
2pR |
|
|
|
|
||
I1 |
1 |
|
2 |
I2 |
|
|
|
|
|
|
F21 |
|
F12 |
A |
|
|
|
|
|
|
|
R |
B1 |
|
|
|
|
|
|
Рисунок 5.1 |
|
|||
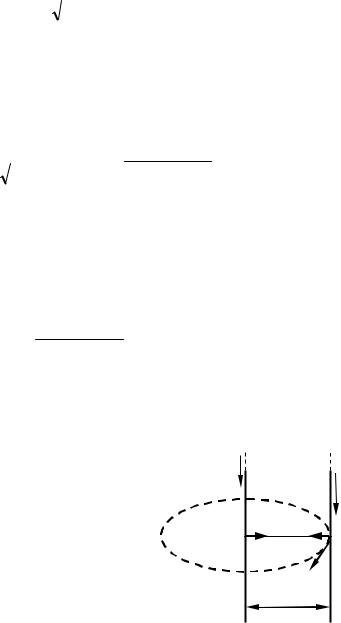
Напрям вектора B1 можна визначити за правилом правого гвинта: коли гвинт
встановити паралельно струму й обертати його так, щоб поступальний рух гвинта був спрямований вздовж струму, то обертання шапочки гвинта буде визначати напрям силових
20