
mah3
.pdfвтакой же мере непрерывное многообразие трех измерений, как
исистема цветовых ощущений. Против этой аналогии возражали, что в первом случае три изменения (измерения) гомогенны (однородны) и могут заменять друг друга, между тем как во втором случае они гетерогенны и не могут заменять друг друга. Но это возражение оказывается неосновательным, если сравнивать пространственное ощущение с цветовым ощущением. Ибо психофизиологические ряды направо — налево и наверху — внизу столь же мало могут заменить друг друга, как ряды красный — зеленый и черный — белый. Только когда сравнивают геометрическое пространство с системой цветов, это возражение становится, по-видимому, основательным. Однако для полной аналогии между созерцаемым пространством и системой цветовых ощущений все же еще многого недостает. В то время, как близкие равные расстояния в пространстве непосредственно познаются нами как таковые, о различии между цветами мы ничего подобного сказать не можем и в последней области не хватает, следовательно, физиологической сравнимости ее частей. Хотя вполне возможно, приложив физический опыт, обозначить каждый цвет системы через три числа, подобно местам в геометрическом пространстве, и таким образом создать для цветов метрическую систему, подобную пространственной, однако все же трудно найти что-либо, что соответствовало бы расстояниям или объемам и имело бы для системы цветов аналогичное физическое значение.
6.Аналогии всегда заключают в себе нечто произвольное, так как распространяются на сходства, которые привлекли наше внимание. Однако вряд ли кто-нибудь станет отрицать аналогию между пространством и временем, и притом как при физиологическом, так и физическом их понимании. В обоих случаях пространство есть непрерывное многообразие трех измерений, а время — непрерывное однородное многообразие. Какой-нибудь физический процесс средней продолжительности, точно определенный известными обстоятельствами, является для нас теперь и во всякое другое время непосредственно равным по продолжительности. Физические процессы, когда-нибудь совпадающие по времени, совпадают по времени и во всякий другой момент. Су-
ществует, следовательно, совмещение во времени, как существует совмещение в пространстве. Существует, следовательно, постоянный физический объект времени, как и постоянный физический объект пространства (твердое тело). Существует не только
пространственная, но и временная субстанциональность. Галилей
пользовался еще физиологическими процессами — пульсом и
375
дыханием — для оценки времени, как некогда пользовались руками и ногами для измерения пространства.
7. Есть также аналогия между пространственными ощущениями — многообразием трех измерений — и ощущениями тонов, составляющими многообразие одного измерения6. Сравнимость различных частей системы ощущений тонов дана в непосредственном ощущении музыкального интервала. Метрическая система, соответствующая геометрическому пространству, получается здесь всего проще, если характеризовать высоту тона логарифмом числа колебаний. Постоянному музыкальному интервалу здесь соответствует выражение:
log— = log«' - logn = log τ - log-c' = konst,
η
где η', η обозначают числа колебаний, a τ', τ — продолжительность колебаний высшего и низшего тона. Разность логарифмов означает здесь длину, которая остается постоянной при перемещении вдоль линии тонов. Постоянный субстанциональный физический объект, который мы ощущаем как интервал, определен для нашего уха временно, между тем как аналогичный объект для чувства зрения и осязания определен пространственно. Мера пространства только потому нам кажется проще, что мы ту же самую длину, которая остается постоянной для пространственного чувства, выбрали и как основную меру в геометрии, между тем как к изменениям в области тонов мы приходим лишь окольным физическим путем.
8. Теперь необходимо, помимо сходных черт, указать и на различия в многообразиях, между которыми мы провели аналогию. Рассматривая время и пространство как многообразия ощущений, мы находим, что объекты, движение которых обнаруживается изменением качеств времени и пространства, характеризуются вместе с тем и другими ощущаемыми качествами: цветами, осязательными свойствами, тонами и т. д. Если же проводить полную аналогию между зрительным пространством и, например, ощущениями тона, то получается следующая странная вещь: в первой области локальные качества должны выступить одни, без прочих соответствующих объектам ощутимых качеств, т. е. так, как будто возможно было видеть какое-нибудь место или определенное движение, не видя объекта, занимающего это место или совершающего это движение. Так как однако локальные ка-
На эту аналогию я обратил внимание в 1863 году при изучении органа слуха и с тех пор проследил ее далее. См. «Анализ ощущений» (изд. С. Скирмунта).
376
чества представляют собою ощущения органов, которые могут быть возбуждены только вместе с чувственными качествами7, то упомянутая аналогия не является особенно заманчивой. Для математика, оперирующего многообразиями, не представляет существенной разницы, движется ли объект определенного цвета непрерывно в оптическом пространстве или какой-нибудь предмет, занимающий определенное место, непрерывно изменяясь, проходит многообразный ряд цветов. Но для физиолога и психолога эти случаи весьма различны и не только по указанному выше, но и вследствие еще одного обстоятельства. Система локальных качеств нам весьма привычна, между тем как систему цветовых ощущений мы представляем себе только с трудом и искусственно на основании научных исследований. Цвет кажется нам вырванным членом многообразия, порядок которого для нас непривычен.
9. Многообразия, сравниваемые здесь с пространством, представляют, как, например, система цветов, тоже три измерения или меньшее их число. В самом пространстве мы находим поверхности — многообразия двух измерений — и линии — многообразия одного измерения, а математик на своем обобщающем языке может сюда причислить и точки, как многообразия нулевого измерения. Но не представляет никакого затруднения рассматривать аналитическую механику, как то и было сделано, как аналитическую геометрию четырех измерений (четвертое измерение — время). Вообще отнесенные к координатам уравнения аналитической геометрии легко внушают математику мысль распространить такого рода рассуждения на какое угодно большее число измерений. И физика могла бы рассматривать протяженную материальную непрерывность, каждой точке которой можно приписать определенную температуру, силу притяжения, магнитный и электрический потенциал и т. д., как часть, как вырезку многообразия многих измерений. Мы знаем из истории науки, что оперирование такими символическими образами никоим образом нельзя считать делом совершенно бесплодным.
Символы, которые сначала не имели как будто никакого смысла, постепенно -- так сказать, при мысленных экспериментах над ними — получили ясное и точное значение. Вспомним, например, отрицательные дробные и переменные показатели степени и подобные тому случаи, в которых именно этим путем были достигнуты важные и существенные расширения понятия, которые иначе были бы или совершенно не достигнуты или достигнуты гораздо позже. Вспомним так называемые мнимые ве-
См. стр. 332-333.
377
личины, которыми давно оперировали и достигали даже важных результатов, прежде чем были в состоянии придать им вполне определенный и даже наглядный смысл. Но символическое изображение имеет, правда, и известный недостаток, заключающийся в том, что слишком легко упустить совершенно из виду изображенный в символе объект и оперировать знаками, которым порой никакого объекта не соответствует8.
10. Нетрудно подняться до Римановского представления непрерывного многообразия и измерений и удается даже части такого многообразия реализовать и сделать наглядными. Пусть αΐ 5 аъ аъ,
я4,.... <VH СУТЬ какие-нибудь элементы (ощущаемые качества, вещества и т. д.). Если представить себе эти элементы соединенными во всех возможных отношениях, то каждое отдельное такое соединение может быть представлено следующим выражением:
а2а2 |
*п+\ |
|
причем коэффициенты а удовлетворяют уравнению
а{ +я2 +я3 + ... ап+1 =1.
Так как n коэффициентов а можно выбрать произвольно, то совокупность соединений из n + 1 элементов представляет непрерывное многообразие n измерений9. В качестве коорди-
Я должен сознаться, что, когда я был молодым студентом, меня возмущал каждый вывод при помощи символов, значение которых не было вполне ясно и наглядно. Но историческое изучение способно уничтожить склонность к мистике, легко развивающуюся в случае малосознательного применения таких методов: оно знакомит с эвристическим значением их и в то же время гносеологически выясняет, в чем именно заключается помощь, которую они оказывают. Символическое изображение какого-нибудь вычисления имеет для математика то же значение, какое имеет модель или наглядная рабочая гипотеза для физика. Символ, модель, гипотеза параллельны тому, что должно быть изображено. Но этот параллелизм может заходить далее или может быть проведен далее, чем это предполагалось первоначально при выборе этого средства. Так как то, что подлежит изображению, и средство изображения все же вещи различные, то мы в одном замечаем то, что оставалось бы в другом скрытым. На операцию а2/3 трудно напасть непосредственно. Но вычисление с такими символами приводит к тому, что этот символ получает понятный смысл. В течение многих_йесятилетий оперировали, по примеру Эйлера, выражениями как cpsx + V-1 · sin x.и степенями с мнимыми показателями. Это продолжалось до тех пор, пока в стремлении к взаимному приспособлению мысли и символа не прорвалась, наконец, yArgancfa в 1806 году зревшая в течение столетия идея, что отношение можно рассматривать с точки зрения величины и направления, и тогда оказалось, что v-1 есть среднее пропорциональное направления между +1 и —1.
Если бы шесть основных цветовых ощущений были совершенно независимы друга от друга, то система цветовых ощущений представляла бы многообразие пяти измерений, но так как они образуют три пары противоположных цветов, то эта система соответствует многообразию трех измерений.
378
нат какой-нибудь точки, элемента этого многообразия можно
рассматривать выражения формы — или |
например |
а' |
|
log —- . Но при выборе определения расстояния или других
понятий, аналогичных геометрическим, пришлось бы поступать весьма произвольно, если бы опыт о соответственном многообразии не учил нас, что известные метрические понятия имеют реальное значение и поэтому должны быть предпочитаемы. Так обстоит, например, дело в геометрическом пространстве с вытекающим из постоянства объема тел определением10 элемента расстояния — ds2 = dx2 + dy2 + dz2, a в звуковых ощущениях — с упомянутым уже выше логарифмическим выражением. В большинстве случаев подобных искусственных построений отсутствуют такие опорные пункты, и все исследование оказывается поэтому бесплодным. Аналогия с пространством теряет вследствие этого в полноте, плодотворности и полезности.
11. Риман развил мысли Гаусса еще и в другом направлении, исходя из исследования последнего относительно кривых поверхностей. Меру кривизны данной поверхности в данной
точке Гаусс11 выразил через К = —, где ds обозначает элемент ds
исследуемой поверхности, а АУ — элемент поверхности сферы, принятой за 1, предельные радиусы которого параллельны предельным нормалям элемента ds. Эта мера кривизны может так-
же быть выражена в форме К = |
|
, где pl 5 p2 обозначают |
|
Pi *Р2
главные радиусы кривизны исследуемой поверхности в данной точке. Особый интерес представляют поверхности, мера кривизны которых имеет во всех точках одно и то же значение, поверхности с постоянной мерой кривизны. Если представлять поверхности как бесконечно тонкие, нерастяжимые, но сгибаемые тела, то поверхности с равной мерой кривизны могут при сгибании быть наложены друг на друга; так, например, можно плоский лист бумаги обернуть вокруг цилиндра или конуса, но этот лист бумаги не может быть наложен на поверхность шара. При этой деформации и даже при любом сгибании измерительные отношения длин и углов фигур, начерченных в поверхно-
10См. стр. 359.
11Disquisitiones générales superficies curvas. 1827.
379
сти, остаются без изменения, если только при измерении не выходить из двух измерений поверхности. Мера кривизны поверхности вовсе не зависит от формы последней в третьем измерении пространства, а только от ее внутренних измерительных отношений. Отсюда Риман пришел к мысли распространить понятие меры кривизны на пространство трех и больше измерений. В соответствии с этим он допускает возможность конечных беспредельных пространств с постоянной положительной мерой кривизны, соответственно беспредельной, но конечной шаровой поверхности двух измерений, между тем как, по нашему обычному представлению, бесконечное пространство соответствует бесконечной плоскости с мерой кривизны равной нулю; наконец, третий род пространства соответствовал бы поверхностям с отрицательной мерой кривизны. Фигура, начерченная на поверхности некоторой постоянной кривизны, может быть перемещена без искажения только на этой поверхности; например, сферическая фигура может перемещаться только на этой сфере, и плоская фигура — только в плоскости. Нечто подобное должно, по мысли Римана, существовать и для телесных фигур, для твердых тел. Как это далее развил Гелъмголъц^, последние могли бы свободно передвигаться только в пространствах с постоянной мерой кривизны. Как кратчайшие линии в плоскости бесконечны, на поверхности же шара имеют, как большие круги сферы, некоторую конечную длину и замкнуты (при продолжении возвращаешься к исходной точке), так Риман представляет себе конечным, но беспредельным то, что в трехмерном пространстве положительной кривизны аналогично прямой линии и плоскости. Но здесь встречается некоторое затруднение. Если бы существовало понятие меры кривизны для четырехмерного пространства, то переход к более специальному случаю трехмерного пространства был бы понятен. Но переход от специального к более общему случаю заключает в себе нечто произвольное, и вполне естественно, что различные исследователи пошли здесь различными путями13 (Риман, Kronecker). Уже одно то обстоятельство, что для одномерного пространства — любой крисой линии не существует меры кривизны в смысле ее внутренней меры и что эта мера кривизны является лишь в двумерном пространстве, возбуждает в нас во-
12 |
Über die Tatsachen, welche der Geometrie zu Grunde liegen. Göttinger Nachrich- |
|
ten, 1868, 3 Juni. |
1 |
См. напр. Kronecker, Über Systeme von Funktionen mehrerer Variablen. Ber. d. |
|
Berliner Akademie, 1869. |
380
прос, имеет ли вообще то, что аналогично этому в трехмерном пространстве, какой-нибудь смысл, и в каких пределах? Не впадаем ли мы здесь в иллюзию, оперируя с символами, которым, может быть, вообще ничего действительного не соответствует, во всяком случае ничего наглядного, чем мы могли бы проверять и исправлять наши понятия?
Мы дошли теперь до высших и наиболее общих идей о пространстве и его отношениях к аналогичным многообразиям, которые возникли из взгляда Гаусса на эмпирическое обоснование геометрии. Но развитие этого взгляда имеет двухтысячелетнюю историю, основные факты которой нам удастся, может быть, лучше обозреть с высоты, на которой теперь стоим.
12. Наивные люди, приобретавшие с масштабом в руках первые геометрические познания, придерживались простейших телесных образов — прямой линии, плоскости, круга и т. д. — и исследовали связи измерений на формах, которые можно было рассматривать как комбинации этих простых образов. От них не мог ускользнуть тот факт, что подвижность тела ограничивается, если закрепить одну, затем две точки его, а при закреплении трех точек возможность перемещения совершенно исчезает. Наблюдая в отдельности вращение вокруг оси, вокруг двух точек или вращение в плоскости вокруг одной точки, как и перемещение при постоянном соприкосновении двух точек с прямой линией и третьей точки — с некоторой неподвижной плоскостью, проходящей через эту прямую, учились различать чистое вращение, чистое перемещение и движение, комбинированное из этих двух независимых движений. Первая геометрия, естественно, не была основана на чисто-метрических понятиях, а находилась под сильным воздействием физиологического момента, созерцания14. Этим объясняется появление двух различных основных мер: (прямой) длины и угла (круговой меры). Прямая понималась как твердое подвижное тело (масштаб), а угол — как вращение прямой около другой прямой (измеряемое описанной при этом дугой). Никто, конечно, не требовал особого доказательства равенства описанных этим вращением вертикальных углов. И другие теоремы об углах получались весьма просто. Если мы вращаем прямую b (фиг. 21) около точки пересечения ее с прямой до совпадения с этой последней, описывая угол а, и затем вращаем ту же линию около точки пересечения ее с прямой а до совпадения с этой последней, описывая угол β, то линия b от первоначального своего положения до конечного в а делает поворот на
См. стр. 338, 360.
381
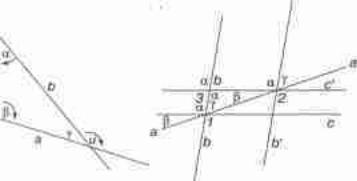
Фиг. 21 |
Фиг. 22 |
угол м; отсюда внешний угол и = а+ ß, a так как и + γ= 2Л, то и α+ β+ γ= 2R15. Если (фиг. 22) перемещать неподвижную систему пересекающихся в точке 1 прямых af b, с в их плоскости до точки 2 так, чтобы прямая а не меняла своего положения, то при этом чистом перемещении ни один угол не меняется. Сумма внутренних углов возникающего при этом треугольника 1 2 3 очевидно равна 2R. То же рассуждение освещает и свойства параллельных линий. Какие-нибудь сомнения вроде тех, действительно ли эквивалентно последовательное вращение вокруг многих точек вращению вокруг одной точки, существует ли вообще чистое перемещение — сомнения, которые оказываются совершенно основательными, если вместо (Евклидовой) плоскости взять поверхность с кривизной, отличной от нуля, — не могли, конечно, возникнуть на этой ступени у наивного исследователя, открывшего эти отношения. Рассмотрение движений твердых тел, которого Евклид тщательно избегал и вводил только в скрытом виде в принципе совмещения, еще и в настоящее время является самым целесообразным средством при элементарном преподавании геометрии. Наилучший путь для усвоения учащимися знаний есть тот, которым эти знания были некогда добыты.
13. Здоровое, наивное понимание исчезло и в обработке геометрии произошли существенные изменения, как только она
С. R. Kosack, Beiträge zu einer systematischen Entwicklung der Geometrie aus der Anschauung. Nordhausen, 1852. — Работу эту любезно доставил мне профессор F. Pietzker в Нордгаузене. — Подобные же простые выводы можно найти у Bernharde Beckefb (Leitfaden für den ersten geometrischen Unterricht in der Geometrie. Frankfurt a. M., 1874) и в другой работе того же автора: Über die
Methode des geometrischen Unterrichts. Frankfurt a. M. 1845. — Первую из этих работ я получил благодаря любезности М. Шустера в Ольденбурге.
382
стала предметом мышления ученых специалистов. Прежде всего оказалось необходимым для удобства собственного обзора привести знания в систему, отделить непосредственно познанное от выводимого и выведенного и ясно указать ход вывода. В целях преподавания были поставлены во главу простейшие знания, легче всего поддающиеся усвоению и не подлежащие, как казалось, сомнению и отрицанию, и на них обоснованы другие. Эти основные положения старались ограничить самым необходимым, как мы то видим в системе Евклида. При этом стремлении обосновать каждое знание на другом и только самое немногое предоставить непосредственному познанию, геометрия постепенно отрывалась от той эмпирической почвы, на которой она зародилась. Привыкли знание, полученное путем выводов, ценить выше знания, полученного из непосредственного воззрения, и, наконец, стали требовать доказательств для положений, в которых никто серьезно не сомневался. Так возникла --по преданию, в ограждение от нападок софистов — логически совершенная, законченная система Евклида. Но при этом искусственном нанизывании положений на произвольно выбранную нить вывода не только были намеренно скрыты пути исследования, но и остались неотмеченными многократные органические связи геометрических учений16. Система скорее способна была воспитывать боязливо бесплодных педантов, чем плодотворно и производительно работающих исследователей. Положение дела ничуть не улучшилось, когда схоластика, предпочитавшая рабски комментировать продукты чужого ума, приучила людей к весьма
малой чувствительности относительно рациональности основных допущений, но зато к тем большему вниманию к логической форме вывода. От этого настроения болсе или менее страдает вся эпоха от Евклида вплоть до Гаусса.
16 Система Евклида подкупала своими логическими преимуществами, вследствие чего оставались незамеченными недостатки ее в иных отношениях. Великие исследователи вплоть до современной эпохи увлекались примером Евклида и в ущерб науке при изложении результатов своих исследований старались скрыть пути этих последних. Но науке не соответствуют искусственные приемы адвокатов. Научно изложение, в котором все мотивы мыслей так изложены, что значение и правильность их могут быть всегда проверены. Учащегося не следует вводить в науку с полузакрытыми глазами. Вследствие этого среди философов и дидактиков Германии явилась здоровая реакция, исходившая главным образом от Гербарта, Шопенгауэра и Тренделенбурга. Это течение старалось ввести в преподавание большую наглядность, более генетический метод и логически более прозрачные выводы. См. современные сочинения:
M. Pasch (Vorlesungen über neuere Geometrie. Leipzig, 1882), D. Gilbert (Grundlagen der Geometrie. Leipzig, 1899).
383
14. Среди положений, на которых Евклид построил свою систему, находится так называемое пятое требование (обозначенное так же, как 11 аксиома): «две прямые, пересеченные третьей таким образом, что сумма внутренних углов, лежащих по одну сторону секущей, меньше двух прямых углов, при достаточном продолжении пересекаются на этой стороне». Евклиду легко удается доказать, что две прямые, образующие с третьей, секущей равные соответственные углы, не пересекаются, параллельны. Но обратное положение, что две параллельные образуют со всякой секущей равные соответственные углы, ему приходится уже обосновать на пятом требовании. Это обратное положение равнозначуще с положением, что через точку можно провести к прямой только одну параллельную ей. Так как с помощью этого обратного положения доказывается, что сумма углов треугольника равна 2R, и так как из этого последнего положения опять-та- ки вытекает первое, то этим ясно обнаруживается связь названных положений и выясняется фундаментальное значение пятого требования для геометрии Евклида.
15.Пересечение слабосходящихся прямых лежит за пределами построения и наблюдения. Понятно поэтому, что последователи Евклида, приученные им к строгости логических выводов, ввиду важности утверждения, заключающегося в пятом требовании, уже в античную эпоху старались доказать это утверждение или заменить его положением, непосредственно очевидным. От Евклида вплоть до Гаусса было предпринято множество бесплодных попыток вывести содержимое пятого требования из остальных допущений Евклида. Зрелище чрезвычайно возвышенное: движимые исключительно чистым стремлением к научному выяснению, люди на протяжении многих столетий занимаются отыскиванием источника познания, в правильности которого ни один теоретик и ни один практик на самом деле не сомневался серьезно вплоть до настоящего дня. С напряжением мы следим за этими настойчивыми проявлениями этической силы научного стремления и с радостью наблюдаем, как неудачи мало-помалу приводят исследователей к мысли, что только опыт есть истинная основа геометрии. Проследим это развитие на нескольких примерах.
16.К исследователям, имеющим большие заслуги в учении о параллельных линиях, принадлежат итальянец Saccheri и немецкий математик Lambert. Чтобы ясно показать способ, которым оба они приступают к этому вопросу, заметим предварительно, что существование прямоугольников и квадратов не может быть доказано без помощи пятого требования, хотя нам и кажется,
384
