
коллоквиум по математике 1семестр
.docx1)Матрица-прямоугольная таблица чисел,состоящая из m-строк,n-столбцов.
М-у
имеющую m-строк
и n-столбцов
назыв М-ей
размера
m n.
М из одной строки назыв мат.строкой.
М,все эл-ты кот=0,назыв нулевой М-ей. М-а
назыв квадратной,если m=n.Квадр-я
М назыв симметричной,если aik=ajk.
а11,a22,…,aij,..,amn
образуют главную диагональ квадр Ма-цы.
Диагональной
назыв квадр М,у кот все эл-ты,кроме
диагональных,=0. Единичной
М-цей назыв диагон М-а у кот все эл-ты гл
диагонали =1. Кв М имеющая n-строк
и n-столбцов
назыв М-ей
порядка
n.
М-а АТ
назыв
транспонированной к М-е А,если каждая
её строка явл столбцом М-ы А.
n.
М из одной строки назыв мат.строкой.
М,все эл-ты кот=0,назыв нулевой М-ей. М-а
назыв квадратной,если m=n.Квадр-я
М назыв симметричной,если aik=ajk.
а11,a22,…,aij,..,amn
образуют главную диагональ квадр Ма-цы.
Диагональной
назыв квадр М,у кот все эл-ты,кроме
диагональных,=0. Единичной
М-цей назыв диагон М-а у кот все эл-ты гл
диагонали =1. Кв М имеющая n-строк
и n-столбцов
назыв М-ей
порядка
n.
М-а АТ
назыв
транспонированной к М-е А,если каждая
её строка явл столбцом М-ы А.
Действия:линейными
операциями над М явл операц слож-я,вычит,умнож
на число.Слож-е и вычит М определенно
только для М одинаков размерности.1)Две
М А и В=, если = их соответств э-ты.2)Умнож-е
М на число:
 .3)Слож
и вычит: А+В=С.Сij=аij+вij.;Св-ва
лин.операц:1)А+В=В+А-коммутативность.2)(А+В)+С=А+(В+С)-ассоциативность.3)А+(-А)=0.4)А*1=А.5)А+0‘=А.6)α*(А+В)=αА+αВ,α-дейст.число.20.Умнож.М.
Произведение двух матриц A и B
обозначается символом AB
и определяется равенством
AB=
.3)Слож
и вычит: А+В=С.Сij=аij+вij.;Св-ва
лин.операц:1)А+В=В+А-коммутативность.2)(А+В)+С=А+(В+С)-ассоциативность.3)А+(-А)=0.4)А*1=А.5)А+0‘=А.6)α*(А+В)=αА+αВ,α-дейст.число.20.Умнож.М.
Произведение двух матриц A и B
обозначается символом AB
и определяется равенством
AB=


Произв-е
М А на В определено только в том
случае,когда число столбцов М А=числу
строк М В.В результате получим М АВ у
которой строк столько же как в А,а столб
как в В; АВ≠ВА;ЕА=АЕ=А;АО=ОА=О.Св-ва
опер умнож:
1)(АВ)С=А(ВС).2)(αА)В=α(АВ)=А(αВ).3)(А+В)С=АС+ВС.4)С(А+В)=СА+СВ.
2. if из ∆ вычеркнуть iстроку и jстолбец на пересечении кот стоит эл-т аij и сдвинуть оставшиеся ряды, то получим ∆ 2-го порядка назыв минором и обозначаемым Мij.
Алгебраическим дополнением Аij в ∆ назыв соответств ему минном взятый со зн +,if i+j четн число,со зн -,if i+j нечет.Аij=(-1)i+jМij. ∆=а11А11+а12А12+а13А13; Св-ва ∆:1) ∆ не измен при транспонировании,т.е. при замене всех его строк соотв столбцами.detA=detAT;2)При перестановке двух стол(строк) ∆ меняет знак.3) ∆ с двумя одинак стол(строк)=0.4)if все эл-ты какого-л стол(стр) обладают общим множителем, то этот множитель можно вынести за знак ∆.5)∆ содержащ нулевую строку(столбец)=0.6)if каждый эл-т какого-л столб(строки) есть сумма двух слагаемых,то ∆=сумме двух ∆.Причем в одном из них столбец состоит из одних слаг,в др из вторых.7)if ∆ содержит две пропорцион строки,то он=0.8)Величина ∆ не изменится,if к эл-ам любого стол(строки) прибавить эл-ты др стол(стр) предварит умноженные на любое число.9) ∆ произв двух М порядка n=произв их ∆.det(AB)=detA*detB.
3.Теорема(о разлож опред по эл-ам стр(стол)): ∆ кВ М=сумме произвед эл-ов какой-л стр(стол) на их алгебраич дополнения.Замечание:Сумма произв-ий эл-ов стр(стол) на алгебраич дополн эл-ов др стр(стол)=0. а11А21+а12А22+а13А23 =0.
Рассмотрим
n–эл-ов.Число
перестановок этих эл-ов=n!.Опр-е:если
в перестановке эл-т с большим номером
стоит раньше,чем эл-т с меньшим номером,то
эти эл-ты образ инверсию. Перестановка,содерж
нечетн(четн) колич инверсий назыв
нечет(четн). Все св-ва ∆ 3-го порядка сохр
для ∆любого порядка.Опред:∆-и
кВ М назыв число обознач ∆= и
равное сумме всех n!
Произвед-й
эл-ов взятых по одному из каждого
стол(стр).
и
равное сумме всех n!
Произвед-й
эл-ов взятых по одному из каждого
стол(стр). ,
взятых со знаком +(-),если перестановка
ij-четное(неч).
,
взятых со знаком +(-),если перестановка
ij-четное(неч).
4.
Пусть
А-кв М порядка n.
М обознач А-1
назыв
обратной А,если АА-1
или А-1А=Е.Теорема(Критерий
сущ-я обр М):Для того чтобы кВ М А имела
обратную необходимо и достаточно,чтобы
её ∆ не был =0.Формула
для нахожд обр М: А-1= ,
∆не=0
,
∆не=0
6.Рассмотрим
М А размера m×n.
Выделим в М А k-строк
и k-столбцов,Эл-ты
стоящие на пересечении выдел стр и
столцов явл эл-ми определителя
k-порядка,кот
назыв минором М k-го
порядка. Обозначим Мk.
Наивысший порядок отличного от 0 минора
назыв рангом М. Из определителя ранга
М
 утвержд-е:
1) 0≤ r
≤min(m;n).
2) r=0,
утвержд-е:
1) 0≤ r
≤min(m;n).
2) r=0, М нулевая. 3)Д/кв М порядка n.
r=n
М нулевая. 3)Д/кв М порядка n.
r=n
 когда определитель М≠0.
когда определитель М≠0.
Элементарные преобразования матриц:1)Транспонирование.2)Перестановка 2 столбоц или строк.3)Умнож-е эл-ов стр/стол на число k≠0. 4)Прибавление эл-ов к какой-н стр/стол к эл-ам др стр /столбца,возможно даже умнож-х на какое-н число.
Перечисленные эл-рные преобразования М-ц рангов М-цы не меняют.
Док-во.Т.к.
ранг-это наивысший порядок
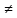 0
минора(т.е. опред-ля),то по св-ам опред-ей
преобразование 1 величины опр-я,соответств
и минора,не меняют. Преобразование 2
меняет знак минора на противоположный(соотв
ранг остается прежний). Преобразование
3 увеличивает величину минора в k
раз. Преобразование 4 величины
опр-ля(минора) не меняет. Т.о.,преобразования
1-4 миноры≠0 останутся ≠0, а миноры
=0,останутся=0.
0
минора(т.е. опред-ля),то по св-ам опред-ей
преобразование 1 величины опр-я,соответств
и минора,не меняют. Преобразование 2
меняет знак минора на противоположный(соотв
ранг остается прежний). Преобразование
3 увеличивает величину минора в k
раз. Преобразование 4 величины
опр-ля(минора) не меняет. Т.о.,преобразования
1-4 миноры≠0 останутся ≠0, а миноры
=0,останутся=0. ранг М не изменится.
ранг М не изменится.
7. Теорема Кронекера-Капелли:Для того чтобы произвольная СЛУ была совместна необходимо и достаточно,чтобы ранг М А=рангу расшир М,т.е. r(A)=r(A/B)
8. Две СЛУ назыв эквивалентными, если они обе несовместны или имеют одинаковое колич-о реш-й.
Элементарные преобразования систем:1)замена i-уравнения j. И наоборот.
2)Прибавление к i-уравнению j-уравнения, умноженного на некоторое число.
Теорема:Эл-ые преобраз-ия 1,2 сохраняют эквивалентность линейных систем.Т.о, Если одна система полученна из другой с помощью конечного числа эл-ых преобразований, то эти системы эквивалентны.
Метод Гаусса(метод последовательного исключения неизвестных) состоит из двух этапов.На первом этапе система приводится к ступенчатому виду.На втором-идёт последовательное определение неизвестных из этой ступенчатой системы.
9.Вектор-направленный отрезок(пара упорядоченных точек).Растояние между нач-ом и концом вектора назыв его длиной(модулем). Пара векторов назыв коллинеарными,если они лежат на // прямых. Нулевой вектор коллинеарен любому вектору. Три вектора назыв компланарными, если существует пл-ть кот-й они //. Два вектора назыв равными, если они коллинеарны, имеют одинаковые длины и одинаково направлены.
Действия
над векторами:1)Вектор
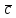 ,соединяющий
начало первого вектора
,соединяющий
начало первого вектора
 с концом второго
с концом второго
 ,
называется суммой векторов a
и
b.Это
правило сложения назыв-т правилом
треугольника.Если
век-ра a
и b
не коллинеарны и их начала совмещены в
одной точке,то их сумма явл диаг-ю
параллелограмма, построенного на
векторах a
и b(правило
параллелограмма).2)Вычитание.Вычисть
а-b
означает найти c,
такой что с+b=a.
3)Произ-м
числа α на
,
называется суммой векторов a
и
b.Это
правило сложения назыв-т правилом
треугольника.Если
век-ра a
и b
не коллинеарны и их начала совмещены в
одной точке,то их сумма явл диаг-ю
параллелограмма, построенного на
векторах a
и b(правило
параллелограмма).2)Вычитание.Вычисть
а-b
означает найти c,
такой что с+b=a.
3)Произ-м
числа α на
 назыв b,
такой что 1)
назыв b,
такой что 1)
 =
= .
2)a
и b-коллинеарны.
3)a
и b
одинаково направл,если α
.
2)a
и b-коллинеарны.
3)a
и b
одинаково направл,если α и противоположно напр,если α
и противоположно напр,если α .
.
Св-ва:1)
 +
+ =
= +
+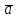 .2)(a+b)+c=a+(b+c).3)a+0=a.
4)a+(-1)a=0. 5)(αβ)a=α(βa),для
α,β
.2)(a+b)+c=a+(b+c).3)a+0=a.
4)a+(-1)a=0. 5)(αβ)a=α(βa),для
α,β
 R. 6)(α+β)a=αa+βa.7)α(a+b)=αa+αb. 8)1a=a
R. 6)(α+β)a=αa+βa.7)α(a+b)=αa+αb. 8)1a=a
10.Рассмотрим
систему векторов а1,а2,...аk
и
люб числа α1
α2,…αk
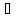 R.
Выражение α1а1+α2а2+…+αkak
назыв линейной комбинацией векторов
a1,…ak,
а числа αi(i=
R.
Выражение α1а1+α2а2+…+αkak
назыв линейной комбинацией векторов
a1,…ak,
а числа αi(i= )-коэффиц
этой комбинации. Если
)-коэффиц
этой комбинации. Если
 =α1
=α1 +α2а2+…αkak
то
говорят,что вектор а разложен по векторам
а1,а2,…аk.
+α2а2+…αkak
то
говорят,что вектор а разложен по векторам
а1,а2,…аk.
11. Базисом в пространстве назыв любая упорядоч-я тройка некопланарных векторов(е1,е2,е3). Базисом на пл-ти назыв любая упор-я пара неколлинеарных векторов.Базис на прямой-любой её ненулевой вектор.Утверждение1.При сложении векторов координаты векторов складываются,а при умнож-и вектора на число координаты умножаются на это число.Утв2)Система век-ов а1…аk явл линейнозависимой когда один из век-ов этой системы есть линейная комбинация остальных.Утв3)а)Любые 2 коллин век-ра лин-о зависимы и наоборот:любые 2 лин-о зависимых коллинеарно.б)Любые 3 компланарных век-ра лин-озависимы и наоборот:любые 3 лине-завис-х век-ра-компланарны.
ДСК назыв совокупность точки и базиса. Прямоуг-й ДСК назыв-т совокупность точки и ортонормированного базиса.Базис е1,е2,е3 назыв ортонормированным,если вектора еi ортогоальны и их длины=1.
12.
Cкалярным
произв a
и b
назыв число = произведению их длин на
cos
угла между ними.
 ^
^ .
.
Св-во:1)Перестановочное:
(ab)=(ba).2)(а,
а)= 2;
2;
 ;
3)
;
3)
 ,если
один и век-ов=0 или вектора
,если
один и век-ов=0 или вектора
 .;
4)α
.;
4)α +β
+β ,
, =α
=α
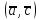 +β
+β

Вещественное линейное пространство назыв Евклидовым,если в нём определенно скалярн произв-е векторов.
Два вектора явл ортогональными,когда их скалярное произв-е =0
Во всяком n-мерном Евклидовом пространстве существует ортонормировый базис.
Проекцией
вектора а на b
назыв длина
 умножен на cos
угла образован
умножен на cos
угла образован
 и
и
 .
Прba=
.
Прba= cos(a^b).
cos(a^b).
13.
Векторным произведением [ ]
векторов
]
векторов
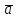 и
и
 назыв
назыв
 ,такой
что:
,такой
что:
 ;2)
;2)
 ,
,
 ,
3)
,
3)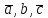 -правая
тройка. Упорядоченная тройка векторов
a,b,c
назыв правой,если с конца третьего
вектора С кратчайший поворот от первого
вектора а
ко второму вектору b
виден совершающимся против часовой
стрелки. В противном случае тройка
векторов левая.
-правая
тройка. Упорядоченная тройка векторов
a,b,c
назыв правой,если с конца третьего
вектора С кратчайший поворот от первого
вектора а
ко второму вектору b
виден совершающимся против часовой
стрелки. В противном случае тройка
векторов левая.
Длина
результата векторн произв-я численно
равна S
параллелограмма построенного на векторах
 .
.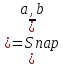
Св-ва:1)некомутативность. .[a,b]= -[b,a]. 2)Д/любых векторов a,b и любого числа λ: [λa, b]= λ[a,b], [a, λb]=λ[a,b].3)Дистрибутивность: [a+b,с]= [a,с]+ [b,с].4)Необходимое и достаточное условие коллинеарности двух векторов a и b равенство 0 векторн произведения. [a,b]=0
Если
a
и b
заданы своими координатами в прямоуг
ДСК,т.е.
 (а1,а2,а3),b(b1,b2,b3),то
их векторное произведение можно найти
через формулу вычисления через координаты
со множителями [a,b]=
(а1,а2,а3),b(b1,b2,b3),то
их векторное произведение можно найти
через формулу вычисления через координаты
со множителями [a,b]= .
.
Условие
коллинеарности векторов в координатах
ортонормированного базиса,благодаря
формуле вычисл через координаты со
множителями,можно записать так

14.
Смешанным
произведением
3 векторов a,b,c
назыв число,кот получается при умножении
векторного произведения
 cкалярно
на
cкалярно
на
 ,
т.е. (
,
т.е. ( )= (
)= ( ). Cв-во:
1)(a,b,c)=0,
тогда и только тогда,когда a,b
и с компланарны.2)операции скалярного
и векторного умножения в смешан произвед-и
можно менять местами.([a,b],c)=(a,[b,c]).3)Круговая
перестановка 3х
сомножителей
смеш произв-я не меняет его
значения.Перестановка же двух соседних
сомножителей меняет знак произведения
на противоположный.4) (α a1+βa2
,
b,c)=α
(a1,b,c)+β(a2,b,c).Если
a,b,c
некомпланарны,то
). Cв-во:
1)(a,b,c)=0,
тогда и только тогда,когда a,b
и с компланарны.2)операции скалярного
и векторного умножения в смешан произвед-и
можно менять местами.([a,b],c)=(a,[b,c]).3)Круговая
перестановка 3х
сомножителей
смеш произв-я не меняет его
значения.Перестановка же двух соседних
сомножителей меняет знак произведения
на противоположный.4) (α a1+βa2
,
b,c)=α
(a1,b,c)+β(a2,b,c).Если
a,b,c
некомпланарны,то



 тройка.
Если a,b,c
заданы своими координатами в
ортонормированном базисе
a(a1,b1,c1),b(a2,b2,c2),c(a3,b3,c3),то
смешан произв-е можно посчитать следующим
образом:
(
тройка.
Если a,b,c
заданы своими координатами в
ортонормированном базисе
a(a1,b1,c1),b(a2,b2,c2),c(a3,b3,c3),то
смешан произв-е можно посчитать следующим
образом:
( )=
)= .
.
15. Линейное пространство назыв n-мерным, когда в нём существуют n-независ-х лин векторов,а любые n+1 векторов уже будут лин-о зависимыми.
Совокупность из n-линейнозавис-х векторов назыв базисом.
Переход
от старого
базиса к новому
задается М перехода (
 ).
При
чем коэф-ты разложения новых базисных
векторов по старому базису явл столбцами
данной матрицы. Тогда координаты любого
вектора Х в старом базисе выраж-ся через
его координаты в новом базисе по формуле:
).
При
чем коэф-ты разложения новых базисных
векторов по старому базису явл столбцами
данной матрицы. Тогда координаты любого
вектора Х в старом базисе выраж-ся через
его координаты в новом базисе по формуле:
 =А
=А
Итог.Множество векторов с действительными компонентами,в кот определены операции сложение векторов и умнож-е вект на число,удовлетворяющее св-ам 1-8 назыв векторным пространством.
Замечание.Под a,b,c можно рассматривать не только векторы,но и эл-ты любой природы.В этом случае,соответствующее множество эл-ов назыв линейным пространством.
17. Общее ур-е прямой. Ах+Ву+С=0
Угол
м/у прямыми
означает найти угол м/у их норм-ми
векторами:

18.
Для
любой точки М(x,y,z),
лежащей на данной прямой, вектор М0М
=
{x
- x0,y
- y0,z
- z0)
коллинеарен направляющему вектору
а(l,m,n).
Поэтому имеют место равенства:![]() называемые
каноническими
уравнениями
прямой в пространстве.
называемые
каноническими
уравнениями
прямой в пространстве.
Ур-е
прямой в отрезках:
 1
1
Формула
вычисл-я расстояния
от точки
с координа-и (x0,y0)
до
прямой
Ax+By+C=0:
d=
19.
Ур-е
прямой,проход ч/з
2 точки:![]() .
.
Условие
параллельности прямых:если
l1//
l2,
то вектора тоже параллельны,т.е.
линейнозависимы.Значит их координаты
пропорциональны,т.е.
![]() ; Условие перпендикулярности прямых:
если l1﬩
l2
то
; Условие перпендикулярности прямых:
если l1﬩
l2
то
 ,т.е.
скалярное произведение=0
,т.е.
скалярное произведение=0
20. Линии 2 порядка:Окружность: (х-х0)2 +(y-y0)2=R2 – уравнение окруж-ти с центром (x0,y0) и радиусом R.
Эллипсом
назыв множество
точек на пл-ти сумма расстояний от
которых до двух данных точек называемых
фокусами есть величина постоянная
большая чем расстояние м-у фокусами.Ур-е
эллипса с большой и малой полуосью:
 +
+ =1
=1
21.
Гиперболой
назыв
множество точек на пл-ти модуль разности
расстояние от кот-х до 2х
данных точек назыв фокусами есть величина
постоянная меньшая чем расстояние м-у
фокусами.Каноническое ур-е гиперболы:
 -
-
 =1
=1
Параболой назыв множ-во точек на пл-ти равноудал-х на данной прямой называемой директрисой, и от данной точки назыв-ой фокусом.Канонич-е ур-е П: y2 =2px
23.Общее
ур-е пл-ти:Ax+By+Cz+D=0.Условие
параллельности плоскостей
заключается в параллельности нормалей:![]() а
условие
перпендикулярности плоскостей
– в перпендикулярности нормалей или
равенстве нулю их скалярного произведения:
A1A2
+ B1B2
+ C1C2
= 0.
а
условие
перпендикулярности плоскостей
– в перпендикулярности нормалей или
равенстве нулю их скалярного произведения:
A1A2
+ B1B2
+ C1C2
= 0.
24.
 Это
уравнение, которому удовлетворяют
координаты х,
у, z
любой точки, лежащей на искомой плоскости,
является уравнением
плоскости, проходящей через три данные
точки.
Это
уравнение, которому удовлетворяют
координаты х,
у, z
любой точки, лежащей на искомой плоскости,
является уравнением
плоскости, проходящей через три данные
точки.
Расстояние
от
любой
точки М0(x0,y0,z0)
до пл-ти Q:
Ax+By+Cz+D=0
находится по формуле: d=

27.Угол
м/у плоск-ми:![]()
