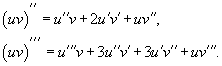1. непр.ф-ииПусть и.

Ф-ия непрерывна в точке , если для любогосущ-еттакое, что для любого

Ф-ия непрерывна на множестве , если она непрерывна в каждой точке данного множества.

В этом случае говорят, что ф-ия классаи пишут:или, подробнее,.

3. Т. о промежуточном значении если непрерывная ф-ия, определённая на вещественном интервале, принимает два значения, то она принимает и любое значение между ними. дана непрерывная ф-ия на отрезке Пусть такжеи без ограничения общности предположим, чтоТогда для любогосущ-еттакое, что.

4. непр.элем.ф-ий Целая и дробная рациональные ф-ии. Непрерывность f(x)=const и f(x)=x непосредственно ясна. На основании теоремы о произведении непрерывных функций вытекает непрерывность любого одночленного выражения ax^m, по теореме о сумме непрерывных функций - непрерывность мн-чла a₀xⁿ + a₁x_n-1 + ... +a_n-1 + a_n. Непрерывность данных функций имеет место на всем интервале . Частное двух мн-чловнепрерывно всюду, кроме точекb₀x^m + b₁x^m-1 +...+ b_m-1x + b_m = 0 (в этих точках - либо разрыв 2-го рода, либо устранимый разрыв).

Показательная ф-ия y=a^x(a>1) монотонно возрастает на всем интервале . Ее значения заполняют весь интервал. Из существования логарифма сл-т непрерывность данной ф-ии.

Логарифмическая ф-ия . Рассмотрим случайa>1. Эта ф-ия возрастает при , и принимает любое значение из. Отсюда сл-т ее непрерывность.

Степенная ф-ия . При возрастанииx от 0 до возрастаетили убываетна интервале. Следовательно, данная ф-ия непрерывна.

Тригонометрические ф-ии ,,,,,. Остановимся на ф-ии. Ее непрерывность на отрезкевытекает из ее монотонности, а также из факта (устанавливаемого геометрически), что при этом она принимает все значения от -1 до 1. То же относится к любому промежутку. Следовательно, ф-иянепрерывна для всех значенийx. Аналогично - для ф-ии . По свойствам непрерывных функций вытекает непрерывность функций. Исключение для первых двух функций - значенияx вида , при которых, для других двух - значения вида, при которых.

Обратные тригонометрические ф-ии ,,,. Первые две непрерывны на, остальные - на

5. Рассмотрим функцию  , определенную на некотором промежутке. Ф-иянепрерывна в точке , если предел ф-ии в точкеравен значению ф-ии в этой точке,.

ПРИМЕР 1.  Доказательство непрерывности ф-ии в точке

Односторонние пределы ф-ии в точке.

Ф-ия, непрерывная в каждой точке промежутка , называетсянепрерывной на промежутке. Если ф-ияопределена на промежутке,, то при исследовании поведения ф-иив окрестности точкиимеет смысл говорить о пределе ф-ии  в точкесправа, а при исследовании в окрестности точки- о пределе ф-ии в точкеслева. Числоназываетсяпределом справа ф-ии при , стремящемся к, если для любого положительного числа, как бы мало оно ни было, сущ-ет такое положительное число, что для всех, удовлетворяющих неравенству, справедливо неравенство. Говорят “предел справа ф-ии в точке” и обозначают. Аналогично говорят “предел слева ф-иив точке ” и обозначают , если для любого положительного числа, как бы мало оно ни было, сущ-ет такое положительное число, что для всех, удовлетворяющих неравенству, справедливо неравенство. Для существования предела ф-ии в точке, необходимо и достаточно, чтобы существовали и совпадали односторонние пределы ф-ии в этой точке. По той же схеме вводится понятие непрерывности слева и непрерывности справа. Ф-ия, опрн-ая на отрезке,, непрерывна справа в точке, еслии непрерывна слева в точке, если. Для того чтобы ф-ия была непрерывна в точкенеобходимо и достаточно, чтобы односторонние пределы ф-ии в точке совпадали со значением ф-ии в этой точке:. Если хотя бы одно из равенств нарушается, говорят о разрыве в точке.

ПРИМЕР 2.  Вычисление односторонних пределов

Классификация разрывов.

Если хотя бы одно из равенств нарушается, говорят о разрыве в точке. Еслии односторонние пределы конечны, то разрыв в точкеназываетсяустранимым. Если и оба односторонние пределы конечны, то говорят оскачке ф-ии в точке . Устранимый разрыв и скачок называютсяразрывами первого рода. Если один из односторонних пределов бесконечен или не сущ-ет, то разрыв называется разрывом второго рода. Так же, как для предела и непрерывности, говорят о разрыве слева и разрыве справа.

6.откр.изамк.мн. Определение 1: Множество М ∈ Ε называется открытым, если для любого у ∈ М найдётся такое ε > 0, что окрестность y по ε строго меньше М С помощью кванторов определение запишется следующим образом: М ∈ Ε — открытое, если    ∀ у∈М   ∃ ε>0 :  U_ε(y) < M

Простым языком — открытое множество состоит из внутренних точек. Примерами открытого множества являются пустое множество, прямая, интервал (а, b)

Определение 2: Точка x* ∈ E называется граничной точкой множества М, если в любой окрестности точки х содержатся точки как из множества М, так и из его дополнения. Теперь с помощью кванторов: х*∈ E — граничная точка, если ∀U_ε(x) ∩ М ≠ ∅ и ∀U_ε(x) ∩ Е\М

Определение 3: Множество называется замкнутым, если ему принадлежат все граничные точки. Пример — отр. [a, b]

Стоит отметить, что существуют множества, которые одновременно и открытые, и замкнутые. Это, например, всё множество действительных чисел и пустое множество (позднее будет доказано, что это 2 возможных и единственных случая).

Докажем несколько теорем, связанных с открытым и замкнутым множествами.

Т. 1: Пусть множество А — открытое. Тогда дополнение к множеству А является замкнутым множеством. Доказательство: Обозначим дополнение множества А как множество В: В = Е\А Доказывать будем от противного. Предположим, что В — незамкнутое. Тогда сущ-ет граничная точка х*, которая не принадлежит В, а значит — принадлежит А. По определению граничной точки окрестность х* имеет пересечение как с В, так и с А. Однако с другой стороны х* является внутренней точкой открытого множества А, поэтому вся окрестность точки х* лежит в А. Отсюда делаем вывод, что множества А и В пересекаются не по пустому множеству. Такого быть не может, поэтому наше предположение неверно и В является замкнутым множеством, ч. т. д. В кванторах доказательство можно записать короче: Предположим, что В — незамкнутое, тогда: (1) ∃ х∈А*:х∈A ⇒ ∀U_ε(x) ∩ В ≠ ∅ (определение граничной точки) (2) ∃ х∈А*:х∈A ⇒ ∀U_ε(x) ⊂ А ≠ ∅ (определение открытоко множества) Из (1) и (2) ⇒ А ∩ В ≠ ∅. Но А ∩ В = А ∩ Е\А = 0. Противоречие. В — замкнутое, ч. т. д.

Т. 2: Пусть множество А — замкнутое. Тогда дополнение к множеству А является открытым множеством. Доказательство: Обозначим дополнение множества А как множество В: В = Е\А Доказывать будем от противного. Предположим, что В — замкнутое множество. Тогда любая граничная точка лежит в В. Но так как А — также замкнутое множество, то все граничные точки принадлежат и ему. Однако точка не может одновременно принадлежать множеству и его дополнению. Противоречие. В — открытое множество, ч. т. д. В кванторах это выглядеть будет следующим образом: Предположим, что В — замкнутое, тогда: (1) ∀ х∈А*:х∈A (из условия) (1) ∀ х∈А*:х∈В (из предположения) Из (1) и (2) ⇒ А ∩ В ≠ ∅. Но А ∩ В = А ∩ Е\А = 0. Противоречие. В — открытое, ч. т. д.

Т. 3: Пусть множество А — замкнутое и открытое. Тогда А = Е или А = ∅ Доказательство: Начнём записывать подробно, но сразу использую кванторы. Предположим, что множество С — замкнутое и открытое, причём С ≠ ∅ и С ≠ Е. Тогда очевидно, что С ⊆ Е. (1) ∃ х∈А*:х∈С ⇒ ∀U_ε(x) ∩ Е\С ≠ ∅ (определение граничной точки, которая принадлежит С) (2) ∃ х∈А*:х∈A ⇒ ∀U_ε(x) ⊂ В (определение открытого множества С) Из (1) и (2) сл-т, что Е\С ∩ С ≠ ∅, но это неверно. Противоречие. С не может быть одновременно и открытым, и замкнутым, ч. т. д.

8.пон.пр.г.и.м.см.пр. Средней скоростью изменения ф-ии при переходе независимой переменной от значенияк значениюназывается отношение приращенияф-ии к приращениюнезависимой переменной, то есть

Истинной или мгновенной скоростью изменения ф-ии при заданном значении независимой переменнойназывается предел, к которому стремится средняя скорость изменения ф-ии при стремлению к нулю приращения аргумента:

(Механический смысл производной)

Пусть задан путь движения материальной точки. Скорость данной материальной точки в момент времениесть пр-ия от путипо времени:

Пр-ия ф-ии , вычисленная при заданном значении, равна тангенсу угла, образованного положительным направлением осии положительным направлением касательной, проведенной к гр-ику этой ф-ии в точке с абсциссой:

0

9.Выв.табл.произв.ст.,пок,лог.ф-ий

10.8дл.триг.ф-ий

Производные тригонометрических и обратных тригонометрических функций

11.фор.д.пол.прир.ф.,пр.с,р,пО: Полным приращением ф-ии z =(х, у) называется разность

Замечание. В общем случаеПусть, например,

Аналогично полное приращение ф-ии

Пр-ия суммы (разности) функций

Пр-ия алгебраической суммы функций выражается следующей теоремой.

Пр-ия суммы (разности) двух дифференцируемых функций равна сумме (разности) производных этих функций:

Пр-ия конечной алгебраической суммы дифференцируемых функций равна такой же алгебраической сумме производных слагаемых. Например,

Пр-ия произведения функций.

Пусть u(x) и u(x) - дифференцируемые ф-ии. Тогда произведение функций u(x)v(x) также дифференцируемо и

Пр-ия произведения двух функций не равана произведению производных этих функций.

Пр-ия частного функций.

Пусть u(x) и u(x) - дифференцируемые ф-ии. Тогда, если v(x) ≠ 0, то пр-ия частного этих функций вычисляется по формуле

12.ос.пр.выч.пр. 1. Константу можно выносить за знак производной.

2. Пр-ия суммы/разности.

Пр-ия суммы/разности двух функций равна сумме/разности производных от каждой из функций.

Пример

Больше примеров решений →

3. Пр-ия произведения.

Пример

Больше примеров решений →

4. Пр-ия частного.

Пример

Больше примеров решений →

5. Пр-ия сложной ф-ии.

Пр-ия сложной ф-ии равна производной этой ф-ии по промежуточному аргументу , умноженной на производную от промежуточного аргументапо основному аргументу.

и имеют производные соотв. в точкахи. Тогда

Т.

(О производной обратной ф-ии)

Если ф-ия непрерывна и строго монотонна в некоторой окрестности точкии дифференцируема в этой точке, то обратная ф-ияимеет производную в точке, причем.

13св.меж.сущ.пр.икас. По аналогии с односторонними пределами вводится понятия левой и правой производных. Если ф-ция y=f(x) непрерывна слева в точке и сущ-ет предел, где, то этот предел называютлевой производной ф-ции f в точке и обозначают. Аналогично, если ф-ция y=f(x) непрерывна справа в точке, то пределназываютправой производной ф-ции f в точке и обозначают.

Прямые, проходящие через точку с угловыми коэффициентамииназывают соотв.левой и правой касательными к гр-ику ф-ции y=f(x) в точке . Из существования производнойсл-т существованиеии рав-во:==. В этом случае правая и левая касательные к гр-ику ф-ции y=f(x) в точкесовпадают с касательной в точке.Обратное утверждение также верно.

Если то говорят, что ф-ция y=f(x) имеет в точкепроизводную, равнуюи пишут. Аналогично, если, то.

В случае, когда илиговорят, что ф-ция y=f(x) имеет в точкебесконечную производную. (иногда добавляют : определенного знака).

ОДНОСТОРОННЯЯ КАСАТЕЛЬНАЯ к гр-ику ф-ии y=f(х) в точке М₀ — правая (или левая) касательная, т. е. предельное положение секущего луча М₀М, когда точка М стремится к М₀, оставаясь справа (соотв. слева) от точки М₀. На рис. 178 М₀N — правая и М₀Р — левая касательные.

14.диф.ф-ии,пон.диф,геом.см.12.Дифференци́руемая (в точке) фу́нкция — это ф-ия, у которой сущ-ет дифф-ал (в данной точке). Дифференцируемая на некотором множестве ф-ия — это ф-ия, дифференцируемая в каждой точке данного множества Ф-ия одной переменной является дифференцируемой в точкесвоей области определения, если сущ-ет такая константа, что для любой точкиверно

при этом число неизбежно равно производной

Ф-ия переменныхявляется дифференцируемой в точкесвоей области определения, если для любой точкисуществуют такие константы, что

где .

В этой записи ф-ия

является дифф-алом ф-ии в точке, а числаявляютсячастными производными ф-ии в точке, то есть

где — вектор, все компоненты которого, кроме-ой, равны нулю, а-ая компонента равна 1.

• Знак дифф-ала используется в выражении для интеграла . При этом иногда (и не вполне корректно) дифф-алвводится как часть определения интеграла.

• Также знак дифф-ала используется в обозначении Лейбница для производной . Это обозначение мотивировано тем, что для дифф-алов ф-иии тождественной ф-ииверно соотношение

Геометрический смысл дифф-ала

 

На гр-ике ф-ии возьмем произвольную точкуи дадим аргументуприращение . При этом ф-ия получит приращение(на рисунке отр.).

Проведем касательную к кривой в точкеи обозначим угол ее наклона к осичерез, тогда. Из треугольниканаходим, т.е..

Таким образом, дифф-ал ф-ии численно равен приращению ординаты касательной, проведенной к гр-ику ф-ии в данной точке, когда аргументполучает приращение.

15.осн.ф.выч.дифф. 1. Константу можно выносить за знак дифф-ала.

2. Дифф-ал суммы/разности.

Дифф-ал суммы/разности функций равен суме/разности дифф-алов от каждого из слагаемых.

3. Дифф-ал произведения.

4. Дифф-ал частного.

5. Дифф-ал константы равен нулю.

17.

Производные высшего порядка

Пусть y = f(x) является дифференцируемой функцией. Тогда пр-ия также представляет собой функцию от x. Если она является дифференцируемой функцией, то мы можем найти вторую производную ф-ии f, которая обозначается в виде Аналогично, если f '' сущ-ет и дифференцируема, мы можем вычислить третью производную ф-ии f: Производные более высокого порядка (если они существуют), определяются как Для нахождения производных высшего порядка можно использовать следующие формулы: В частности, для производной второго и третьего порядка формула Лейбница принимает вид

Производные n-го порядка от основных элементарных функций

Справедливы формулы

Формула Лейбница

Если u и v - n-кратно дифференцируемые ф-ии, то

17.пр.выс.пор. – см.пред. Формула Лейбница для -ой производной произведения двух функций — обобщение правиладифференцирования произведения (и отношения) двух функций на случай -кратного дифференцирования.

Пусть ф-ии и—раз дифференцируемые ф-ии, тогда

где —биномиальные коэффициенты.

Доказательство формулы осуществляется по индукции с использованием правила произведения. В мультииндексной записи формула может быть записана в более общем виде:

Эта формула может быть использована для получения выражения для композиции дифф-альных операторов. В самом деле, пусть P и Q — дифф-альные операторы (с коэффициентами, которые дифференцируемы достаточное число раз) и . ЕслиR также является дифф-альным оператором, то справедливо равенство:

Непосредственное вычисление дает:

18.дифф.выс.пор.,отс.вар-тиДля ф-ии, зависящей от одной переменной второй и третий дифф-алы выглядят так:

Отсюда можно вывести общий вид дифф-ала n-го порядка от ф-ии :

При вычислении дифф-алов высших порядков очень важно, что есть произвольное и не зависящее от, которое при дифференцировании посл-т рассматривать как постоянный множитель.

Дифф-ал высшего порядка ф-ии нескольких переменных

Если ф-ия имеет непрерывные частные производные второго порядка, то дифф-ал второго порядка определяется так:.

Символически общий вид дифф-ала n-го порядка от ф-ии выглядит следующим образом:

где , апроизвольные приращения независимых переменных. Приращениярассматриваются как постоянные и остаются одними и теми же при переходе от одного дифф-ала к следующему. Сложность выражения дифф-ала возрастает с увеличением числа переменных.

Неинвариантность дифф-алов высшего порядка

При  ,-й дифф-ал не инвариантен (в отличие от инвариантности первого дифф-ала), то есть выражениезависит, вообще говоря, от того, рассматривается ли переменнаякак независимая, либо как некоторая промежуточная ф-ия другого переменного, например,.

Для доказательства неинвариантности дифф-алов высшего порядка достаточно привести пример. При n = 2 и  :

• если  — независимая переменная, то

• если  и

1. 

2. при этом,  и

С учётом зависимости , уже второй дифф-ал не обладает свойством инвариантности при замене переменной. Также не инвариантны дифф-алы порядков 3 и выше.

19.т.фермаДля любого натурального числа урав.

не имеет решений в целых ненулевых числах .

20.т.ролляЕсли вещественная ф-ия, непрерывная на отрезке и дифференцируемая на интервале, принимает на концах этого интервала одинаковые значения, то на этом интервале найдётся хотя бы одна точка, в которой пр-ия ф-ии равна нулю. Если ф-ия на отрезке постоянна, то утверждение очевидно, поскольку пр-ия ф-ии равна нулю в любой точке интервала.

Если же нет, поскольку значения ф-ии в граничных точках сегмента равны, то согласно теореме Вейерштрасса, она принимает своё наибольшее или наименьшее значение в некоторой точке интервала, то есть имеет в этой точке локальный экстр., и по лемме Ферма, в этой точке пр-ия равна 0.

21.т.лагранжа Пусть группа G конечна и H — её подгруппа. Тогда порядок G равен порядку H, умноженному на количество её левых или правых классов смежности (индекс). Количество правых и левых смежных классов любой подгруппы водинаково и называетсяиндексом подгруппы в(обозначается).

Количество правых и левых смежных классов любой подгруппы водинаково и называетсяиндексом подгруппы в(обозначается).

Порядок любой подгруппы конечной группы делит порядок.

Из того, что порядок элемента группы равен порядку циклической подгруппы, образованной этим элементом, сл-т, что порядок любого элемента конечной группы делит порядок. Это следствие обобщаеттеорему Эйлера и малую теорему Ферма в теории чисел.

Группа порядка , где—простое число, циклична. (Поскольку порядок элемента, отличного от единицы, не может быть равен 1, все элементы, кроме единицы, имеют порядок , и значит, каждый из них порождает группу.)

1. 23.т.лопиталялибо;

2. и дифференцируемы в проколотой окрестности;

3. в проколотой окрестности ;

4. сущ-ет ,

тогда сущ-ет .

Пределы также могут быть односторонними.

Отношение бесконечно малых

Докажем теорему для случая, когда пределы функций равны нулю (то есть неопределённость вида ).

Поскольку мы рассматриваем ф-ии итолько в правой проколотой полуокрестности точки, мы можем непрерывным образом их доопределить в этой точке: пусть. Возьмём некоторыйиз рассматриваемой полуокрестности и применим к отрезкутеорему Коши. По этой теореме получим:

,

но , поэтому.

Дальше, записав определение предела отношения производных и обозначив последний через , из полученного равенства выводим:

для конечного предела и

для бесконечного,

что является определением предела отношения функций.