
- •ВВЕДЕНИЕ
- •§ 1. Матрицы и простейшие операции над ними
- •Операции над матрицами
- •§ 2. Определители, их основные свойства и методы вычисления
- •2.1 Определители второго порядка
- •Свойства определителей второго порядка
- •2.2 Определители третьего порядка
- •2.3 Понятие об определителях высших порядков
- •§ 3. Обратная матрица и ее вычисление
- •4.2 Метод Крамера
- •4.3 Метод Гаусса
- •§ 5. Векторы, линейные операции над векторами
- •Линейные операции над векторами
- •§ 6. Проекция вектора на ось. Теоремы о проекциях
- •§ 7. Линейная зависимость векторов. Базис
- •7.1 Базис на плоскости и в пространстве
- •7.2 Прямоугольный Декартов базис. Декартова система координат
- •7.3 Направляющие косинусы вектора
- •7.4 Радиус-вектор
- •7.5 Условие коллинеарности двух векторов
- •7.6 Простейшие задачи
- •§ 8. Скалярное произведение векторов
- •8.2 Косинус угла между векторами
- •§ 9. Векторное произведение векторов
- •§ 10. Смешанное произведение трех векторов
- •§ 2. Прямая на плоскости
- •2.1 Общее уравнение прямой и его исследование
- •2.4 Уравнение прямой, проходящей через две данные точки
- •2.6 Уравнение прямой в отрезках
- •2.7 Нормальное уравнение прямой
- •2.8 Расстояние от точки до прямой
- •§ 3. Плоскость
- •3.1 Общее уравнение плоскости
- •3.2 Неполные уравнения плоскости
- •3.3 Уравнения плоскости в отрезках
- •3.4 Нормальное уравнение плоскости
- •3.6 Расстояние от точки до плоскости
- •§ 4. Прямая в пространстве
- •4.1 Уравнение линии в пространстве
- •4.2 Векторное уравнение прямой. Параметрические уравнения прямой
- •4.3 Канонические уравнения прямой
- •4.4 Уравнения прямой, проходящей через две точки
- •4.6 Прямая и плоскость в пространстве
- •§ 5. Плоские кривые второго порядка
- •5.1 Окружность
- •5.2 Эллипс
- •5.3 Гипербола
- •5.4 Парабола
- •§ 6. Преобразование системы координат на плоскости
- •6.1 Параллельный перенос осей координат
- •6.2 Поворот осей координат на угол α
- •§ 7. Полярная система координат на плоскости
- •8.1 Сфера
- •8.2 Цилиндрические поверхности
- •8.3 Конические поверхности
- •8.4 Поверхность вращения
- •8.5 Эллипсоид
- •8.6 Гиперболоид
- •8.7 Параболоид
- •Глава III МАТЕМАТИЧЕСКИЙ АНАЛИЗ
- •§ 1. Логическая символика, множества и операции над ними
- •§ 2. Функции и их классификация
- •Элементарные функции
- •§ 3. Абсолютные величины и соотношения, связанные с ними
- •Свойства модуля действительного числа
- •§ 4. Последовательность. Характер изменения переменных величин
- •§ 5. Понятие о пределе переменной
- •§ 6. Окрестность точки
- •§ 7. Предел функции в точке
- •§ 8. Односторонние пределы функции в точке
- •§ 9. Свойства функций, имеющих предел
- •§ 10. Бесконечно малые и бесконечно большие функции
- •§ 11. Основные теоремы о пределах
- •§ 12. Предел дробно-рациональной функции
- •§ 13. Первый замечательный предел
- •§ 14. Второй замечательный предел
- •§ 15. Сравнение бесконечно малых функций
- •§ 16. Непрерывность функции
- •§ 17. Операции над непрерывными функциями
- •§ 18. Свойства функций, непрерывных на отрезке
- •§ 19. Производная функции одной переменной
- •19.2 Основные свойства производной
- •19.3 Производная сложной функции
- •19.4 Производная обратной функции
- •19.5 Производная функции, заданной параметрическими уравнениями
- •19.6 Геометрический смысл производной
- •19.7 Уравнения касательной и нормали к линии
- •19.8 Дифференцирование элементарных функций
- •19.9 Производная степенно-показательной функции
- •19.10 Дифференцирование неявной функции
- •19.11 Производные высших порядков
- •19.12 Правила Лопиталя
- •19.13 Основные теоремы для дифференцируемых функций
- •19.14 Необходимые и достаточные условия монотонности функции. Экстремумы функции
- •19.15 Наибольшее и наименьшее значения функции на отрезке
- •19.16 Выпуклость и вогнутость функции
- •19.17 Формула Тейлора
- •§ 20. Дифференциал функции одной переменной
- •20.1 Дифференциал и его геометрический смысл
- •20.2 Свойства дифференциала функции
- •20.3 Дифференциал сложной функции. Свойство инвариантности
- •20.4 Приближенное вычисление с помощью дифференциала
- •20.5 Дифференциалы высших порядков
- •§ 21. Функции многих переменных
- •21.1 Понятие функции нескольких переменных
- •21.2 Непрерывность функции двух переменных
- •21.3 Дифференцирование функции двух переменных
- •21.5 Полный дифференциал функции двух переменных
- •21.6 Приближенное вычисление с помощью полного дифференциала
- •21.7 Производные высших порядков функции двух переменных
- •21.9 Неявная функция. Дифференцирование неявной функции
- •21.10 Градиент функции многих переменных и его свойства
- •21.11 Экстремум функции нескольких переменных
- •ПЕРЕЧЕНЬ КОНТРОЛЬНЫХ ВОПРОСОВ
- •КОНТРОЛЬНЫЕ ЗАДАНИЯ
- •Вариант 1
- •Контрольная работа № 1
- •Контрольная работа № 2
- •Вариант 2
- •Контрольная работа № 1
- •Контрольная работа № 2
- •Вариант 3
- •Контрольная работа № 1
- •Контрольная работа № 2
- •Вариант 4
- •Контрольная работа № 1
- •Контрольная работа № 2
- •Вариант 5
- •Контрольная работа № 1
- •Контрольная работа № 2
- •Вариант 6
- •Контрольная работа № 1
- •Контрольная работа № 2
- •Вариант 7
- •Контрольная работа № 1
- •Контрольная работа № 2
- •Вариант 8
- •Контрольная работа № 1
- •Контрольная работа № 2
- •Вариант 9
- •Контрольная работа № 1
- •Контрольная работа № 2
- •Вариант 10
- •Контрольная работа № 1
- •Контрольная работа № 2
- •ПРИЛОЖЕНИЕ
- •Список рекомендуемой литературы
139
Вариант 2
Контрольная работа № 1
1. Даны вершины A(−7; 3) , B(5; − 2) , C(8; 2) треугольника. Требуется найти:
1)длину стороны BC ;
2)площадь треугольника ABC ;
3)уравнение стороны BC ;
4)уравнение высоты, проведенной из вершины A ;
5)длину высоты, проведенной из вершины A ;
6)угол B в радианах с точностью до 0,01.
Сделать чертеж.
2. |
На прямой 3x + 4 y −5 = 0 найти точку, равноудаленную |
от точек |
A(−3; − 2) и B(3; 0) . |
|
|
3. |
Найти прямую, проходящую через точку пересечения |
прямых |
3x − y −1 = 0 , x +3y +1 = 0 и параллельно оси абсцисс. |
|
|
4. Составить уравнение линии, для каждой точки которой сумма расстояний от точек F1 (−1; 3) и F2 (7; 3) есть величина постоянная, которой принадлежит
точка P(6; 27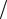 5) . Сделать чертеж.
5) . Сделать чертеж.
5.Найти расстояние фокуса гиперболы x2 −3y2 = 6 , абсцисса которого положительна, от диагоналей прямоугольника с вершинами в точках пересечения гиперболы с эллипсом x2 +3y2 =12 . Сделать чертеж.
6.Дано уравнение параболы y2 − 6x + 2 y −11 = 0 . Сделать параллельный перенос осей координат так, чтобы в новой системе координат XO1Y уравне-
ние параболы приняло вид x2 = ay или y2 = ax . Построить обе системы координат и параболу.
7. Решить систему линейных алгебраических уравнений:
3x + 2 y − z + 2 = 0,2x − y + 3z = 0,
x + 3y − 4z = 0,
а) используя правило Крамера; б) используя матричный метод; в) используя метод Гаусса.
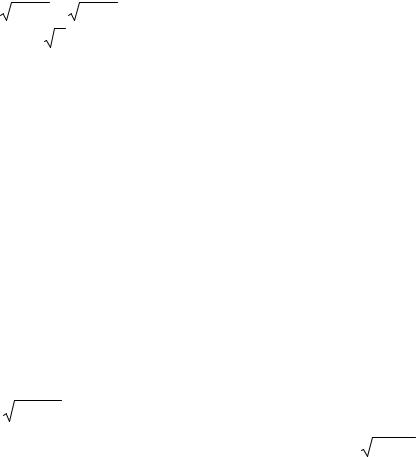
140 8. Даны векторы ar ={4; 7; 8} , b ={9; 1; 3} , c ={2; − 4; 1}, dr ={1; −13; −13} в
некотором базисе. Показать, что векторы a , b , c образуют базис, и найти координаты вектора d в этом базисе.
9. Даны вершины A1 (3;3;9) , A2 (6;9;1) , A3 (1; 7;3) , A4 (8;5;8) пирамиды. Тре-
буется найти средствами векторной алгебры:
1)длину ребра A1 A2 ;
2)угол между ребрами A1 A2 и A1 A4 ;
3)площадь грани A1 A2 A3 ;
4)объем пирамиды;
5)уравнение высоты, опущенной из вершины A4 на грань A1 A2 A3 .
Контрольная работа № 2
1. Найти указанные пределы (не пользуясь правилом Лопиталя):
а) |
lim |
2x5 −3x2 |
+5 |
; |
|
б) |
lim |
2x2 |
−5x − |
3 |
; |
|
||
3x5 + 4x2 |
+1 |
|
x2 |
− x −6 |
|
|
||||||||
|
x→∞ |
|
|
|
x→3 |
|
|
|
||||||
в) |
lim |
7 − x − |
7 + x |
; |
г) |
lim sin 4x + sin 2x |
; |
|||||||
|
7x |
|
||||||||||||
|
x→0 |
|
|
|
|
|
x→0 |
|
6x |
|
|
|
||
д) |
lim |
2x |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
x→0 ln(1+ x) |
|
|
|
|
|
|
|
|
|
|
|
||
2. Функция y = f (x) |
задана различными аналитическими выражениями для |
|||||||||||||
различных областей изменения независимой переменной. Найти точки разрыва функции, если они существуют. Построить график функции.
|
2 |
− 4, |
x < −2; |
x |
|
||
y = 3x + 2, − 2 ≤ x ≤ 0; |
|||
12 − x2 , |
x > 2. |
||
|
|
|
|
3. Найти производные dydx :
|
|
|
x |
|
|
|
− |
1 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||
а) |
y = |
|
|
|
; |
б) |
y = 5 |
sin |
x |
; |
|
|
− x2 |
|
|||||||||
|
4 |
|
|
|
|
|
|
|
|
||
в) |
y = ln tg3 π |
; |
г) |
y = 4arctg |
1+ 2x ; |
||||||
|
|
|
6 |
|
|
|
|
|
|
|
|
д) |
(e y − x)2 = x2 + a2 . |
|
|
|
|
|
|
||||

141
4. Найти |
dy |
и |
d 2 y |
для функции, заданной параметрически: |
|
dx |
dx2 |
||||
|
|
|
x = t3 +8t,y = t5 +3t.
5. Продифференцировать данные функции, используя правило логарифмического дифференцирования:
|
а) |
y = (x2 +1)cos |
x ; |
|
|
|
|
|
б) |
y = (x2 − 2) 7 4 + x2 . |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 (12x +3)2 |
|||||||
6. |
Найти указанные пределы, используя правило Лопиталя: |
|
|||||||||||||||||||||||
|
а) |
lim |
|
ln(x − a) |
|
|
|
|
|
|
|
б) |
|
|
|
1 |
|
|
|
|
1 |
|
|
||
|
|
|
; |
|
|
|
|
|
lim |
|
|
|
|
|
|
− |
|
|
. |
||||||
|
|
|
|
|
|
|
|
|
|
−1 |
ln x |
||||||||||||||
|
|
x→a ln(ex − ea ) |
|
|
|
|
|
|
|
|
x→1 |
x |
|
|
|
|
|||||||||
7. |
На линии y = 2x3 − 4x + 7 |
найти точку, в которой касательная к этой ли- |
|||||||||||||||||||||||
нии перпендикулярна прямой |
x + 2 y −3 = 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
8. |
Исследовать методами дифференциального исчисления и построить гра- |
||||||||||||||||||||||||
фики функций: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
а) |
y = x3 −9x2 + 24x −15 ; |
|
|
|
|
|
б) |
y = |
|
|
|
|
x |
. |
|
|
|
|||||||
|
|
|
|
|
|
|
ln |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
||||
9. |
Вычислить приближенно с помощью дифференциала: |
|
|
|
|||||||||||||||||||||
|
|
|
|
x + 5 − x2 |
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
||
|
а) |
y = |
|
|
|
, x = 0,98 ; |
|
|
|
|
б) |
y = x |
|
, |
|
|
x = 2,002 . |
||||||||
|
2 |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
10. |
Найти частные производные дz |
, |
|
дz |
функции z = z(x; y) : |
||||||||||||||||||||
|
|
|
|
|
|
|
дx |
|
|
дy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а) |
z = x2 + xy + y2 ; |
|
|
|
|
|
б) |
z = arctg |
|
x |
. |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
||
11. а) Найти производную сложной функции |
z = f (ϕ(t);ψ (t)) : |
||||||||||||||||||||||||
|
|
|
|
f (x; y) = arccos(x − y) , |
|
ϕ(t) = 3t , |
|
ψ (t) = 4t3 . |
|
||||||||||||||||
|
б) |
Найти частные производные |
|
дz |
, |
дz |
сложной функции |
||||||||||||||||||
|
|
|
дv |
||||||||||||||||||||||
|
|
z = f [ϕ(u; v);ψ (u; v)]: |
|
|
дu |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
f (x; y) = x ln y , |
|
ϕ(u; v) = u cos v , |
ψ (u; v) = u sin v . |
|
|
|
|||||||||||||||||
