Файловый архив студентов. Файловый архив студентов.
1261 вуз, 4624 предмет.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Уфимский Государственный Нефтяной Технический Университет
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:
Mathematics1 reduced.pdf
Скачиваний:
117
Добавлен:
17.03.2015
Размер:
1.9 Mб
Скачать
☆
►Содержание►

69

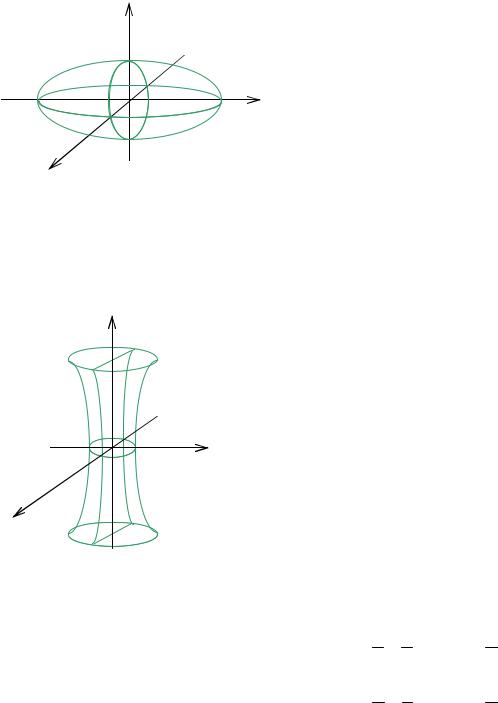
8.5 Эллипсоид

Определение. Эллипсоидом называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравне-

нием (рис. 2.30):

x2

+

y2

+

z2

=1.

(6)

a2

b2

c2

 

 

 

 

Уравнение (6) называется каноническим уравнением эллипсоида.

Величины a , b , c – полуоси эллипсоида. Если они все различны, то эл-

липсоид называется трехосным; если какие-то две из них одинаковы, то эл-

z

 

липсоид является поверхностью враще-

 

ния. Например, если a = b , то осью вра-

 

 

 

 

 

 

 

 

щения будет ось Oz .

c

 

 

 

При a = b < c эллипсоид вращения

 

 

 

 

b

 

называется вытянутым;

a

O

y

при a = b > c – сжатым.

 

 

 

 

Если a = b = c , то эллипсоид пред-

 

 

 

 

ставляет собой сферу.

 

 

 

 

x

 

Точки пересечения эллипсоида с

 

осями координат называются вершинами

Рис. 2.30

 

 

эллипсоида.

8.6 Гиперболоид

Различают однополостной и двуполостной гиперболоид.

z

 

Определение.

Однополостным

ги-

 

 

перболоидом называется поверхность, кото-

 

 

рая в некоторой системе декартовых прямо-

 

 

угольных координат определяется уравнени-

 

 

ем (рис. 2.31):

 

 

 

 

 

 

 

 

 

 

 

 

 

x2

 

y2

 

z2

 

 

 

 

 

 

 

 

+

 

−

 

 

=1.

 

(7)

 

y

 

 

a2

b2

c2

 

 

 

 

 

 

 

 

 

каноническим

 

Уравнение

(7)

называется

 

 

 

 

уравнением однополостного гиперболоида.

x

 

Однополостной

гиперболоид

состоит

 

из прямых, эти прямые называются прямо-

 

 

 

 

линейными

образующими.

Однополостной

 

 

гиперболоид

имеет две

системы

образую-

Рис. 2.31

щих, которые определяются уравнениями:

 

 

x

 

 

z

 

 

 

y

 

α

 

 

+

 

 

 

= β 1

+

 

 

,

 

 

 

 

 

a

 

 

c

 

 

 

b

 

x

 

 

z

 

 

 

y

 

 

 

 

 

 

β

 

 

−

 

 

 

=α 1

−

 

 

,

 

 

 

 

 

 

a

 

 

c

 

 

 

b

 

 

 

 

 

α x + z = β 1 − y ,

a c b

β x − z =α 1 + y ,

a c b

70

где α , β – некоторые числа, не равные одновременно нулю; a , b , c – полу-

оси гиперболоида.

z

 

Через каждую точку однополостного ги-

 

перболоида проходит по одной прямой из ука-

 

 

 

 

 

 

 

 

 

 

занных семейств.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

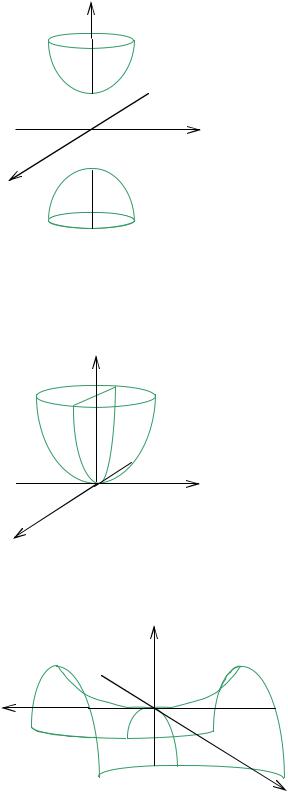
Определение.

 

Двуполостным

гипербо-

 

 

 

 

 

лоидом называется поверхность, которая в неко-

 

 

 

 

 

 

 

 

 

 

торой декартовой системе координат определя-

 

O

y

ется уравнением (рис. 2.32):

 

 

 

 

 

 

 

 

 

 

 

 

 

x

2

 

+

y

2

 

−

z2

= −1.

 

(8)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x

 

 

 

 

 

a2

 

b2

 

c2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Уравнение (8) называется каноническим уравне-

 

 

 

 

 

нием двуполостного гиперболоида.

 

 

 

 

 

 

 

 

 

 

 

 

При

a = b

гиперболоиды

являются по-

Рис. 2.32

 

 

верхностями вращения.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

8.7 Параболоид

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

z

 

 

Определение.

 

Эллиптическим

парабо-

 

 

 

 

 

лоидом называется поверхность, которая в неко-

 

 

 

 

 

торой системе декартовых прямоугольных ко-

 

 

 

 

 

ординат определяется уравнением (рис. 2.33):

 

 

 

 

 

 

 

 

 

 

x2

 

 

 

y2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

+

 

 

 

 

= 2z ,

 

 

(9)

 

 

O

y

где p , q –

 

 

p

 

q

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

положительные числа, называемые

 

 

 

 

 

параметрами параболоида.

 

 

 

 

x

 

 

 

 

 

 

Уравнение (9) называется каноническим уравне-

Рис. 2.33

 

нием эллиптического параболоида.

 

В случае p = q параболоид является поверхностью вращения.

 

 

 

z

 

 

 

 

 

 

 

Определение.

Гиперболиче-

 

 

 

 

 

 

ским параболоидом называется по-

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

верхность, которая в некоторой сис-

 

 

 

O

 

 

 

 

теме

 

декартовых

прямоугольных

 

 

 

 

 

 

 

координат определяется уравнением

x

 

 

 

 

 

 

 

 

(рис. 2.34):

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x2

 

 

y2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

−

= 2z ,

(10)

 

 

 

 

 

y

 

 

 

 

 

 

 

 

 

 

p

 

q

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Рис. 2.34

 

Уравнение (10) называется канони-

 

 

 

 

 

 

 

 

 

 

 

 

ческим уравнением гиперболическо-

го параболоида.

Гиперболический параболоид состоит из прямых, он имеет две системы образующих, которые определяются уравнениями:

71

αβ

x

 

 

y

 

 

 

 

 

 

x

 

 

y

 

 

 

 

+

 

 

 

= 2β z,

 

α

 

 

 

−

 

 

 

= 2β z,

 

 

 

 

 

p

 

 

 

 

 

 

 

 

 

p

 

 

 

 

 

 

 

 

q

и

 

 

 

 

q

 

x

 

y

 

 

 

 

 

x

 

y

 

 

 

 

 

 

 

 

 

 

 

−

 

 

=α,

β

 

+

 

 

=α,

 

 

 

 

 

 

p

 

 

 

 

 

 

 

 

 

p

 

 

 

 

 

 

 

 

q

 

 

 

 

 

 

q

 

где α , β – некоторые числа, не равные одновременно нулю.

Через каждую точку гиперболического параболоида проходит по одной прямой из указанных семейств.

Пример 4. Привести к каноническому виду уравнение

4x2 +9 y2 +36z2 −8x −18y −72z +13 = 0 .

Решение. Сгруппируем члены с одинаковыми координатами:

4(x2 − 2x) +9( y2 − 2 y) +36(z2 − 2z) = −13 .

Дополнив до полных квадратов выражения в скобках, получим:

4(x2 − 2x +1) +9( y2 − 2 y +1) +36(z2 − 2z +1) = −13 + 4 +9 +36 ,

или

4(x −1)2 +9( y −1)2 +36(z −1)2 = 36 .

Произведем параллельный перенос осей координат, приняв за новое начало координат точку O′(1; 1;1) . Формулы преобразования координат име-

ют вид: x = x′+1,

y = y′+1,

z = z′+1. Тогда уравнение поверхности запи-

шется так:

 

 

 

 

 

 

 

x

′2

 

y

′2

 

 

 

4x

′2

+9 y

′2

+36z

′2

= 36

, или

+

+ z

′2

=1.

9

4

 

 

 

 

Это уравнение определяет эллипсоид; его центр находится в новом начале координат, а полуоси соответственно равны 3, 2 и 1.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности