ДЛЯ ЛАБ ПО МАТАНУ

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Уфимский Государственный Нефтяной Технический Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

(b j −619,81)2

e 2 (301,69)

.pdf

Скачиваний:

Добавлен:

17.03.2015

Размер:

820.77 Кб

Скачать

☆

<<< < Предыдущая 1 2 34 / 94 5 6 7 8 9 > Следующая >>>

грубым ошибкам, поэтому при небольшом объеме выборки следует пользоваться интервальными оценками.

Интервальной называют оценку, которая определяется двумя числами – концами интервала, покрывающего оцениваемый генеральный параметр θг .

Доверительным называют интервал, который с заданной надежностью (доверительной вероятностью) γ покрывает оцениваемый генеральный

параметр, то есть с которой осуществляется неравенство

θг −θв

< δ.

Обычно надежность оценки (доверительная вероятность γ) задается.

Причем в качестве γ берут число, близкое к единице (0,95; 0,99; 0,999).

Итак, пусть вероятность того, что

θг

−θв

< δ равна γ, то есть

или

θг −θв

δ)= γ,

(2.8)

P(θв −δ < θг < θв + δ)= γ,

(2.8а)

тогда интервал

(θв −δ;θв + δ) и есть доверительный интервал.

Для

оценки

математического

ожидания

Mг [x]

нормально

распределенной генеральной совокупности X по выборочной средней Mв[x]

при известном среднем квадратическом отклонении σг =

Dг [x]

служит

доверительный интервал.

Mв[x]− t σг

< Mг[x]< M

в[x]+ t σг

(2.9)

σг = δ−

где t

точность оценки; N − объем выборки;

t − это такое

значение

аргумента функции Лапласа Φ(t) (приложение 1), при котором Φ(t)=

Для

оценки

математического

ожидания

Mг [x]

нормально

распределенной генеральной совокупности X по выборочной средней Mв[x]

при неизвестном среднем квадратическом отклонении

σг =

Dг [x]

и (при

объеме выборки N > 30) служит доверительный интервал

Mв[x]− tγ σв

< Mг[x]< M

в[x]+ tγ σв

(2.10)

где t γ

находим по таблице (приложение 2) по заданным N и γ.

Для

оценки среднего

квадратического

отклонения

σг нормально

распределенной генеральной совокупности X с доверительной вероятностью служат доверительные интервалы:

σв (1 −q)< σг	< σв (1 + q)	(при	q <1)	(2.11)
0 < σг	< σв (1 + q)	(при	q >1),
где q − находим по таблице (приложение 3) при заданных N и γ.
Замечание. Для Mг [x]предлагается построить доверительные интервалы
для двух значений вероятности γ = 0,95 и 0,99 . Провести				анализ, как

меняются границы интервалов с увеличением доверительной вероятности.

ПРИМЕР 2.2. Найти точечные и интервальные оценки генерального математического ожидания и генеральной дисперсии, исходя из данных примера 2.1.

1) По данным таблицы 2.5 рассчитываем выборочное математическое ожидание и выборочную дисперсию, среднее квадратическое отклонение.

MB [x]= 0,06 130,666 + 0,14 290 + 0,25 449,333 + 0,18 608,666 +

+0,16 768 + 0,1 927,332 + 0,05 1086,66 + 0,03 1246 +

+0,03 1405,332 = 619,81.

DB [x]= (130,666 −619,81)2 0,06 +(290,0 −619,81)2 0,14 +

+(449,333 −619,81)2 0,25 +(608,666 −619,81)2 0,18 +

+(768 −619,81)2 0,16 + (927,332 −619,81)2 0,1 +

+(1086,66 −619,81)2 0,05 +(1246 −619,81)2 0,03 +

+(1405,332 −619,81)2 0,03 = 91015 .

σB = DB [x]= 91015 ≈ 301,69.

По данным табл. 2.4 вычисляем еще одну точечную характеристику

среднее арифметическое значение нашей выборки X = ∑ xi N : X = 615,80.

i=1

2) Делаем расчет интервальных оценок, то есть будем строить доверительные интервалы с доверительной вероятностью γ.

а) γ = 0,95; σВ = 301,69; MB [x]= 619,81.

Ищем соответствующее значение t γ по таблице в приложении 2 t γ =1,984 .

Точность оценки δ = 1,984 301,69		≈ 59 . Тогда
	100
p(619,81 −59 < MГ[x]< 619,81 +59)= 0,95 ;
p(560,81 < MГ[x]	< 678,81)= 0,95 .
б) γ = 0,99; t γ	= 2,627.
δ = 2,627 301,69	= 77,83.
100

p(619,81 −77,83 < MГ[x]< 619,81 + 77,83)= 0,99 ;
p(531,98 < MГ[x]< 697,64)= 0,99.
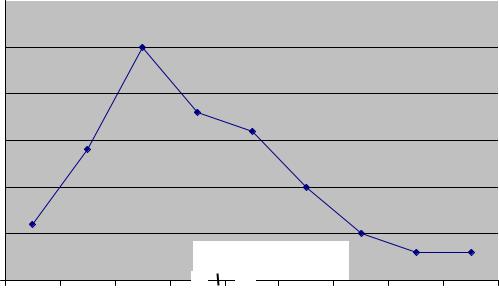
Строим полученные интервалы на полигоне распределения
относительных частот.
μ
0,3
0,25
0,2
0,15
0,1
0,05			Mв[x]= 619,81
0			Mв[x]= 619,81
0	b2	b3	((	))	b6	b7	b8	x
b1	b2	b3	b4	b5	b6	b7	b8	b9

2.3 ЛАБОРАТОРНАЯ РАБОТА № 3

«Проверка гипотезы о законе распределения генеральной совокупности»

В лабораторной работе №1 в результате первичной обработки исходных данных получено эмпирическое распределение (табл. 2.3) и по данным этой таблицы построен полигон относительных частот. Относительные частоты иногда называют эмпирическими вероятностями. Из визуального наблюдения полигона можно сделать один из следующих выводов:

Гипотеза Ао : Генеральная совокупность распределена по нормальному закону;

Гипотеза Во: Генеральная совокупность распределена по показательному закону; Гипотеза Со: Генеральная совокупность распределена по равномерному

закону.

Гипотеза Ао .

Для того, чтобы при заданном уровне значимости α ( γ − доверительная вероятность, то есть вероятность принять верную гипотезу; α − это

вероятность отвергнуть верную гипотезу (α + γ =1)), проверить гипотезу о нормальном распределении генеральной совокупности надо:

1. Вычислить Мв[х], σв (лабораторная работа № 2).

Вычислить

теоретические

вероятности p j

(j =

Поскольку

1, k

плотность распределения для нормального закона есть

f (x)=

e−(x−M[x])2 (2D[x]).

(2.12)

2πσ

Тогда

a j

p j = p (a j−1 < x < a j )=

−(x−MВ[x])2 (2Dв[x])

∫e

2πσв a j−1

e−(b j −MВ[x])2 (2DВ[x])

a j

e−(b j −MВ[x])2 (2DВ[x]) h,

(2.13)

∫dx

2πσ

a j−1

2πσВ

j =

1, k

где a j − границы частичных интервалов;

b j

− середина j −го частичного интервала;

h −длина частичного интервала (см. формулу (2.2)).

3. Составим сводную таблицу на основе данных табл. 2.3 и рассчитанных

теоретических вероятностей:

Таблица 2.6

…

b j

…

μ1

μ2

…

μj

…

μk

← эмпирические вероятности

← теоретические вероятности

…

p j

…

μj

(j =

)

Оценку отклонения

эмпирических

вероятностей

от

1, k

теоретических вероятностей

p j

(j =

)

производим

помощью критерия

1, k

Пирсона χ2 :

χнабл2

. =

(μj

− p j )

∑

(2.14)

p j

j=1

5. По таблице критических точек распределения χ2

(приложение 4)

по

заданному уровню значимости

α и числу степеней свободы

r = k −3 ( k −

количество

подынтервалов)

находим критическое

значение

χкр2

. (α, r)

правосторонней критической области.

Правило 2.1. Если χнабл2 . < χкр2 . , тогда нет оснований отвергать гипотезу A0 о нормальном распределении генеральной совокупности (то есть эмпирические и теоретические частоты различаются незначимо (случайно).

Правило 2.2. Если χнабл2 . > χкр2 ., тогда гипотезу A0 отвергаем.

Гипотеза B0 .

Для того, чтобы при заданном уровне значимости α, проверить гипотезу

опоказательном распределении генеральной совокупности надо:

1.Вычислить MВ[x] (лабораторная работа № 1). Принять в качестве

λпоказательного распределения величину, обратную

выборочной средней:	1
λ =		.	(2.15)
	MВ[x]
			p j (j =		). Поскольку
2. Вычислить теоретические вероятности				1, k

плотность распределения для показательного (экспоненциального) закона есть

f (x)= 0,		при x < 0,		(2.16)
	λ e−λx ,	при x ≥ 0,

тогда		a j
		a j
p j = p (a j−1 < x < a j )= λ ∫e−λ x dx =
		a j−1
= − e−λ x	a j = −(e−λ a j − e−λ a j−1 )		= e−λ a j−1 − e−λ a j ,
= − e−λ x	a j = −(e−λ a j − e−λ a j−1 )		= e−λ a j−1 − e−λ a j ,
	a j−1
	a j−1

где a j (j =1, k)− границы частичных интервалов;

λ − вычисляем по формуле (2.15).

3. Составим сводную таблицу на основе данных табл. 2.3 и рассчитанных


теоретических вероятностей (см. табл. 2.6).					μj (j =		) от
4. Оценку отклонения эмпирических вероятностей						1, k
теоретических вероятностей p j (j =		) производим
	1, k			с помощью критерия
Пирсона χ2 (формула (2.14)).
5. По таблице критических точек распределения χ2				по заданному уровню
значимости α и по числу степеней свободы			r = k − 2		( k − количество
подынтервалов) находим критическое значение			χкр2 .	(α, r)правосторонней

критической области (см. Приложение 4).

Далее анализируем в соответствии с правилами 2.1 и 2.2 (для предыдущей гипотезы).

Гипотеза С0 .

Для того, чтобы при заданном уровне значимости α, проверить гипотезу

оравномерном распределении генеральной совокупности надо:

1.Оценить параметры a и c − концы интервала, в котором наблюдались

возможные значения x , по формулам (через a* и c* обозначены оценки параметров):

a* = MВ[x]−

3 σВ,

с* = MВ[x]+

3 σВ.

(2.17)

2. Вычислить теоретические частоты p j (j =

). Поскольку плотность

1, k

распределения для равномерного закона есть

f (x)=

(2.18)

тогда

c* −a*

p j = p (a j−1 < x < a j )= a∫j

dx =

a j−1 c* − a*

(2.19)

a j

∫dx =

c* − a*

a j−1

где

a j (j =

)− границы частичных интервалов;

1,k

h − длина частичных интервалов.

Получили, что все p j

(j =

)равны одному числу

1, k

c* − a*

3. Составим сводную таблицу на основе эмпирических вероятностей и

рассчитанных теоретических вероятностей (см. табл. 2.6).

μj

(j =

) от

4. Оценку отклонения эмпирических вероятностей

1, k

теоретических вероятностей p j (j =

)

производим с

помощью критерия

1, k

Пирсона χ2 (формула (2.14)).

5. По таблице критических точек распределения χ2

по заданному уровню

значимости

α и по числу степеней свободы r = k −3

( k −

количество

подынтервалов) находим

критические значения

χкр2

. (α, r)

правосторонней

критической области.

Далее анализируем в соответствии с правилами 2.1 и 2.2 (см. Гипотезу А). Замечание 2.1. После составления таблицы 5 необходимо сделать на одном рисунке два графика: ломаную эмпирических вероятностей и кривую

теоретических вероятностей.

Замечание 2.2. Здесь же на этом рисунке рекомендуется нанести:

а) MВ[x]; б) доверительный интервал, построенный для одной из доверительных вероятностей γ (например, для λ = 0,95); в) интервал, построенный по правилу «3-х сигм».

Замечание 2.3. Данный рисунок является наглядным результатом работы, проделанной в Л.Р. 1,2,3.

ПРИМЕР 2.3. Используя критерий согласия Пирсона при уровне значимости α = 0,01, проверить гипотезу о нормальном распределении генеральной совокупности.

1) Переносим из лабораторной работы № 1 полигон распределения относительных частот и табл. 2.5.

X	130,6	290	449,3	608,6	768	927,3	1086,6	1246	1405
μ	0,06	0,14	0,25	0,18	0,16	0,1	0,05	0,03	0,03

μ
0,3
0,25
0,2
0,15
0,1
0,05			Mв[x]
0			Mв[x]
0								x
b1	b2	b3	b4	b5	b6	b7	b8	x
b1	b2	b3	b4	b5	b6	b7	b8

2) Из визуального наблюдения ломаной делаем предположение (ставим гипотезу) о законе распределения генеральной совокупности, то есть

ставим гипотезу H0 : выборка распределена по нормальному закону.

3) Вычислим теоретические вероятности p j . Для этого записываем функцию плотности f (x) для нормального закона:

		1	− (x−MB [x])2
f (x)	=	1	e	2 σB2	.
f (x)	=	2π σB	e		.
Соответственно f (x)=		1	−	(x−619,81)2
		1	e		2
			e	2 (301,69)		или
2	3,14 301,69
− (x−619,81)2
f (x)= 0,001 e 2 (301,69)2 .

p1	= 0,003 1	e
	2π

− (130,666−619,81)2
2 (301,69)2	159,333 =

	1	e−	(1,62)2
= 0,478	1	e−	2 = 0,478 0,1109 = 0,05;
	2 π

p2 = 0,478	1	e
	2 π

	−	(290−619,81)2
	−	2 (301,69)2 = 0,478 0,2203 = 0,105;
		2 (301,69)2 = 0,478 0,2203 = 0,105;

		1			− (449,333−619,819)2
p3	= 0,478	1		e	2 301,692		= 0,478
p3	= 0,478	2	π	e			= 0,478
		2	π
= 0,478 0,3391 = 0,162;
		1			− (608,666−619,819)2
p4	= 0,478	1		e	2 301,692		= 0,478
p4	= 0,478	2	π	e			= 0,478
		2	π
= 0,478 0,3986 = 0,19;
		1			− (768−619,819)2
p5	= 0,478	1		e	2 301,692 = 0,169;
		2 π
		1			− (927,332−619,819)2
p6	= 0,478	1		e	2 301,692		= 0,11;
p6	= 0,478	2	π	e			= 0,11;
		2	π
		1			− (1086,66−619,819)2
p7	= 0,478	1		e	2 301,692		= 0,06;
p7	= 0,478	2	π	e			= 0,06;
		2	π
		1			− (1246−619,819)2
p8	= 0,478	1		e	2 301,692	= 0,02;
p8	= 0,478	2	π	e		= 0,02;
		2	π
		1			− (1405,332−619,819)2
p9	= 0,478	1		e	2 301,692		= 0,007.
p9	= 0,478	2	π	e			= 0,007.
		2	π

1	e−	(0,565)2
1	e−	2	=
2π
1	e−	(0,037)2
1	e−	2	=
2π

4) Составляем табл. 2.7 распределения теоретических вероятностей.

Таблица 2.7

X	130,6	290	449,3	608,6	768	927,3	1086,6	1246	1405
μ	0,06	0,14	0,25	0,18	0,16	0,1	0,05	0,03	0,03
p	0,05	0,105	0,162	0,19	0,17	0,11	0,06	0,02	0,007

Отметим теоретические вероятности на полигоне относительных частот.

	5) Рассчитаем значение критерия χвыб2 . .
	2	=	(0,06 −0,05)2				(0,14 −0,11)2		100 +	(0,25 −0,16)2	100 +
	χвыб.			0,05	100 +		0,11			0,16

+	(0,18 −0,19)2			100 +	(0,16 −0,17)2			(0,1−0,11)2
	0,19				0,17		100 +		0,11	100 +

+	(0,03 −0,03)2			100 +	(0,03	−0,007)2
	0,02				0,007		100 = 0,2 + 0,8 +5,06 + 0,05 +

+0,06 + 0,09 + 0,17 + 0,5 + 7,56 =14,48.

6)Из таблицы «Критические точки распределения χ2 » находим

соответствующее нашим значениям χкр2 . (α, r).

α = 0,01; r = k −3

k = 9 r = 6 . χкр2 . (0,01;6)=16,8.

Сравниваем χвыб2 . и χкр2 . . Так как χвыб2 . < χкр2 . (14,48 <16,8), то гипотеза А0 (выборка распределена по нормальному закону) принимается, по правилу 2.1.

2.4 ЛАБОРАТОРНАЯ РАБОТА № 4 «Расчет параметров корреляционной зависимости»

Две случайные величины могут быть связаны функциональной зависимостью, либо зависимостью другого рода, называемой статистической, либо быть независимыми. Строгая функциональная зависимость для случайных величин реализуется редко, так как обе величины (или одна из них) подвержены различным случайным факторам (даже если среди этих факторов есть общие).

Статистической называют зависимость, при которой изменение одной из величин влечет изменение распределения другой. Если при изменении одной из величин изменяется среднее значение другой, то в этом случае статистическую зависимость называют корреляционной. Значит, корреляционная зависимость есть частный случай статистической зависимости.

Чтобы установить наличие и характер статистической связи между двумя случайными величинами X иY, нужно привести к удобному виду исходный

цифровой материал. Наглядной (удобной) формой представления данных является корреляционная таблица:

							Таблица 2.8
Y	y1	y2	…	y j	…	yl		mx
X
x1	m11	m12	…	m1j	…	m1l		mx1
x 2	m21	m22	…	m2 j	…	m2l		mx2
…	…	…	…	…	…	…		…
xi	mi1	mi2	…	mij	…	mil		mxi
…	…	…	…	…	…	…		…
x k	mk1	mk 2	…	mkj	…	mkl		mxk
my	my1	my2	…	myj	…	myl		m

Здесь	x1 , x 2 ,K, x k ; y1 , y2 ,K, yl –	середины	подынтервалов
сгруппированных выборок X и Y (см.		лабораторную	работу №1);

mij −частота, с которой встречается пара ( xi ; y j ). В последнем столбце и в

последней строке таблицы помещены суммарные частоты, соответствующие значению X = xi и, соответственно, Y = y j , то есть

mxi = mi1 +mi2 +K+mil;
myj	= m1j		+ m2 j +K+ mkj , тогда должно быть
mx	+ mx		+K+ mx		k
mx	+ mx	2	+K+ mx	k	= ∑ mx	i	= m и
1		2		k	i=1	i
					i=1
my	+ my		+K+ my		+K+ my			l
my	+ my	2	+K+ my	j	+K+ my		l	= ∑ my	= m .
1		2		j			l	j=1	j
								j=1

m −общее количество пар значений (xi ; y j ).

Каждая i −я строка табл. 2.8 представляет собой совместно с первой строкой некоторое распределение случайной величиныY, соответствующая

данному значению случайной величиныX = xi . Такое распределение

называется условным распределением. Последняя строка табл. 2.8 совместно с первой строкой образует безусловное распределение случайной величины Y (ее эмпирический закон распределения):

Таблица 2.9

Y	y1	y2		…	y j		…	yl
my	my	my	2	…	my	j	…	my	l
	1		2			j			l

<<< < Предыдущая 1 2 34 / 94 5 6 7 8 9 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
17.03.20151.27 Mб45дипломный проект v1.3.docx
#
14.08.20191.37 Mб5ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 1-30.doc
#
27.10.201811.93 Mб36Длинные нарды - Школа игры.doc
#
08.11.2018671.74 Кб1для заочников практикум.doc
#
17.03.201518.6 Кб16Для курсовой по Сооружениям Лист А4 Форма 2.docx
#
17.03.2015820.77 Кб75ДЛЯ ЛАБ ПО МАТАНУ.pdf
#
17.03.20151.22 Mб102ДМ.doc
#
06.03.201668.79 Кб22добыча нефти и газа.docx
#
06.03.20162.1 Mб63док 2.docx
#
08.11.2018128.51 Кб2доклад по приводу.doc
#
21.04.2015137.81 Кб19ДОКЛАД.docx