
ДЛЯ ЛАБ ПО МАТАНУ
.pdf
σв2 = |
N Dв[x] |
. |
(1.7) |
|
|||
|
N −1 |
|
|
Полученная оценка σв2 - это состоятельная несмещенная выборочная дисперсия, а σв - выборочное среднее квадратичное отклонение.
При выборке малого объема (N < 30) точечная оценка может значительно отличаться от оцениваемого генерального параметра, то есть приводить к грубым ошибкам. Поэтому при небольшом объеме выборки следует пользоваться интервальными оценками.
Пусть найденная (по данным выборки) статистическая оценка θв является оценкой неизвестного генерального параметра θг . Ясно, что θв тем
точнее определяет θг , чем меньше значение разности |
|
θг −θв |
|
. То есть при |
||||||||||||
|
|
|||||||||||||||
|
|
|
|
(δ > 0) чем меньше δ, тем оценка |
|
|
|
|
|
|
||||||
|
θг −θв |
|
< δ |
|
θг точнее. Значит, |
|||||||||||
|
|
|
|
|
||||||||||||
|
положительное число δ характеризует точность оценки. |
|
|
|
||||||||||||
|
Надежностью (доверительной вероятностью) оценки θв называется |
|||||||||||||||
вероятность γ, с которой осуществляется событие |
|
θг −θв |
|
< δ, то есть |
||||||||||||
|
|
|||||||||||||||
|
|
|
|
γ = P( |
|
θг −θв |
|
< δ). |
(1.8) |
|||||||
|
|
|
|
|
|
|||||||||||
|
Обычно надежность оценки (доверительная вероятность γ) задается. |
|||||||||||||||
Причем в качестве γ берут число, близкое к единице (0,95; |
0,99; 0,999). |
|||||||||||||||
Доверительным называется интервал, который с заданной надежностью γ покрывает оцениваемый генеральный параметр. В соотношении (1.8), если
раскрыть |
модуль, |
получается |
P(−δ < θг −θв < δ)= γ |
или |
P(θв −δ < θг < θв + δ)= γ. |
|
|
||
Тогда интервал |
(θв −δ; θв + δ) |
и есть доверительный интервал. |
Из |
|
общих соображений ясно, что длина доверительного интервала будет зависеть от объема выборки N и доверительной вероятности γ.
Для |
оценки |
математического |
ожидания |
Mг [x] |
нормально |
распределенной генеральной совокупности X по выборочной средней Mв[x] |
|||||
при известном среднем квадратическом |
отклонении |
σг = Dг [x] служит |
|||
доверительный интервал: |
|
|
|
|
|
Mв[x]− t |
σг |
< Mг [x]< Mв[x]+ t |
σг |
, |
(1.9) |
|
N |
|
N |
|
|
8
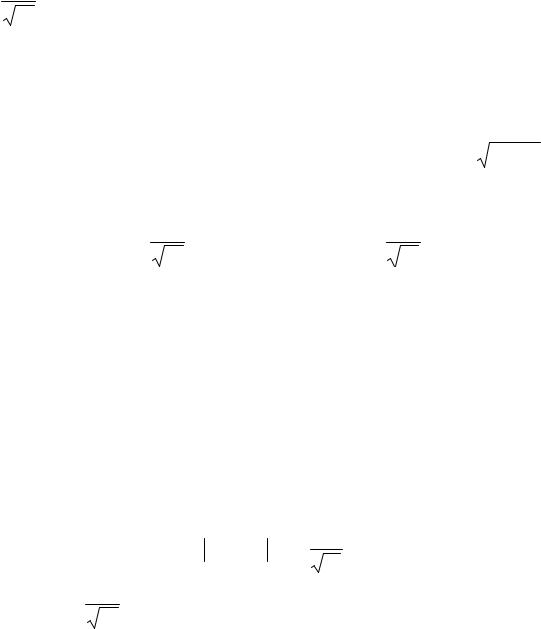
где t σг |
= δ - |
точность оценки; N - |
объем выборки; |
t - такое значение |
||||||
N |
|
|
|
|
|
|
|
γ |
|
|
аргумента функции Лапласа Ф(t) (приложение 1), при котором Ф(t)= |
. |
|||||||||
|
||||||||||
Для |
оценки |
математического |
ожидания |
Mг [x] |
2 |
|
||||
нормально |
||||||||||
распределенной генеральной совокупности X по выборочной средней Mв[x] |
||||||||||
при неизвестном |
среднем квадратическом отклонении |
σг = |
Dг [x] (при |
|||||||
объеме выборки N > 30) служит доверительный интервал: |
|
|
|
|
||||||
|
Mв[x]− t γ σв < Mг [x]< Mв[x]+ t γ |
σв |
, |
(1.10) |
||||||
|
|
|
N |
|
N |
|
|
|
|
|
где t γ находим по таблице (приложение 2) по заданным N и γ. |
|
|
|
|||||||
Для оценки среднего квадратического отклонения σг |
нормально |
|||||||||
распределенной генеральной совокупности X с доверительной вероятностью γ |
||||||||||
служат доверительные интервалы: |
|
|
|
|
|
|
||||
|
σв (1 −q)< σг < σв (1+ q) |
(при q <1); |
|
(1.11) |
||||||
|
0 < σг |
< σв (1 + q) |
(при q >1), |
|
||||||
|
|
|
|
|
||||||
где q – находим по таблице (приложение 3) при заданных N и γ.
Замечание 1.1. Оценку θг − θв |
< t |
σг |
называют классической. Из |
|
|
N |
|
формулы δ = t σNг , определяющей точность классической оценки, можно сделать выводы:
1)при возрастании объема выборки N число δ убывает, значит, точность оценки увеличивается;
2)увеличение надежности оценки γ приводит к увеличению значения
t (так как γ = 2Ф(t) и функция Ф(t) - возрастающая), значит, к возрастанию
δ, то есть к уменьшению точности оценки.
Замечание 1.2. В связи со второй частью замечания 1.1 обычно предлагается строить доверительные интервалы для двух значений вероятности
γ= 0,95 и γ = 0,99. Затем провести анализ, как меняются границы интервалов
сувеличением доверительной вероятности.
9
1.4 ПРОВЕРКА СТАТИСТИЧЕСКОЙ ГИПОТЕЗЫ О ЗАКОНЕ РАСПРЕДЕЛЕНИЯ ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ
Статистической гипотезой H 0 называется любое предположение
относительно закона распределения исследуемой случайной величины X. Гипотезы бывают простые и сложные. Простая гипотеза полностью
определяет закон распределения величины X в отличии от сложной. Гипотезы бывают параметрическими и непараметрическими. В первом
случае мы имеем предположение о параметрах распределения при известном законе, а во втором – о самом виде закона распределения.
ПРИМЕР 1.2. Гипотеза H0 о том, что математическое ожидание нормальной случайной величины равно Mв[x] при условии, что дисперсия Dг [x] известна, является простой параметрической. Если же дисперсия Dг [x] неизвестна, то гипотеза будет сложной параметрической.
ПРИМЕР 1.3. Гипотеза H0 о том, что случайная величина распределена
по нормальному (или по какому-то другому) закону, является сложной непараметрической.
Наряду с выдвинутой гипотезой H0 рассматривают противоречащую ей гипотезу H1 . Если выдвинутая гипотеза H0 будет отвергнута, то имеет место противоречащая ей гипотеза H1 .
Критерием проверки статистической гипотезы называется некоторое правило, позволяющее принять ее или отвергнуть. Причем критерии строятся с помощью случайной величины K (часто именно ее называют критерием), для
которой известно распределение. Наблюдаемым значением критерия K
называют значение критерия, вычисленное по данным выборки. В случае проверки гипотез возможны ошибки:
Ошибка 1-го рода состоит в том, что будет отвергнута правильная гипотеза. Вероятность ошибки первого рода α называется уровнем значимости критерия, по которому производится проверка.
Ошибка 2-го рода состоит в том, что будет принята неправильная гипотеза. Если β - вероятность ошибки второго рода, то величина 1 −β
называется мощностью критерия.
Параметрические гипотезы проверяются с помощью критериев значимости, а непараметрические – с помощью критериев согласия.
Критической областью называется совокупность значений критерия, при которых нулевую гипотезу отвергают. Если уровень значимости α уже выбран и задан объем выборки, то критическую область следует строить так, чтобы мощность критерия была максимальной. Выполнение этого требования должно обеспечить минимальную ошибку второго рода, что более желательно.
Основной принцип проверки статистических гипотез: если K принадлежит критической области – гипотезу H0 отвергают, если же K принадлежит области принятия гипотезы, то гипотезу H0 принимают.
10

Остановимся только на гипотезе о законе распределения генеральной совокупности.
В1.2 при группировке данных выборочной совокупности получена табл.
1.4– эмпирический закон распределения выборки X и по данным этой таблицы построен полигон относительных частот. Относительные частоты иногда называют эмпирическими вероятностями. Из визуального наблюдения
полигона делается вывод (выдвигается гипотеза H0 ) о законе распределения: H0 : генеральная совокупность распределена по нормальному закону.
Ивыдвигается гипотеза, противоречащая гипотезе H0 или ее
отвергающая.
Проверка гипотезы о предполагаемом законе неизвестного распределения производится при помощи специально подобранной случайной величины –
критерия согласия. Разработано несколько таких критериев: χ2 - Пирсона,
Колмогорова, Смирнова и др. Рассмотрим критерий χ2 - Пирсона, как
классический пример применительно к проверке гипотезы о нормальном законе распределения генеральной совокупности.
Будем сравнивать эмпирические и теоретические вероятности. Обычно они различаются. Случайно ли это расхождение? Возможно, что расхождение случайно (незначимо) и объясняется либо малым числом исходных данных, либо способом их группировки или другими причинами. Возможно, что данное расхождение неслучайно (значимо) и объясняется тем, что теоретические вероятности вычислены исходя из неверной гипотезы о нормальном распределении генеральной совокупности.
Пусть нам задан уровень значимости α ( γ - доверительная вероятность,
то есть вероятность принять верную гипотезу; α - это вероятность отвергнуть верную гипотезу, причем α + γ =1). Для того, чтобы при заданном α
проверить гипотезу о нормальном распределении генеральной совокупности, надо вычислить теоретические вероятности. Плотность распределения для нормального закона есть функция:
|
f (x)= |
1 |
|
e−(x−M[x])2 |
(2 D[x]). |
|
(1.12) |
||
|
|
2π σ |
|
|
|
|
|
||
Тогда, пользуясь формулой нахождения вероятности попадания |
|||||||||
случайной величины в интервал: |
|
|
|
|
|
|
|||
|
|
|
p(a < x < b)= ∫b f (x)dx , |
|
|||||
|
|
|
|
|
|
|
a |
|
|
имеем для всех j = |
|
: |
|
|
|
|
|
|
|
1, k |
|
|
|
|
|
|
|||
p j = p(a j−1 |
< x < a j )= |
1 |
|
|
a j |
−(x−Mв[x |
])2 (2 Dв[x]) |
dx = |
|
|
|
∫e |
|
|
|
||||
|
2π σв |
|
a j−1 |
|
|
|
|
||
|
|
|
|
|
|
11 |
|
|
|

= |
1 |
|
|
|
a j |
1 |
e−(x j −Mв[x])2 (2 Dв[x]) h , (1.13) |
e(x j −Mв[x])2 (2 Dв[x]) ∫dx = |
|||||||
|
2π σв |
|
|
a j−1 |
2π σв |
|
|
|
|
a j |
(j = |
|
)- границы частичных подынтервалов (см. 1.2); |
||
|
где |
0; k |
|||||
|
x j |
- середина j −го частичного подынтервала; |
|||||
h - длина частичного подынтервала (см. формулу (1.2)).
Составляется сводная таблица на основе данных табл.1.4 и рассчитанных теоретических вероятностей:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 1.5 |
||||
|
x |
|
x1 |
x 2 |
|
… |
|
|
|
|
x j |
|
|
|
|
… |
|
|
|
x k |
|
|
|
|
|
||||
|
μ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
μ |
1 |
μ |
2 |
|
… |
|
|
|
|
μ |
j |
|
|
|
… |
|
|
|
μ |
k |
эмпирические вероят. |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
p |
|
p1 |
p2 |
|
… |
|
|
|
|
p j |
|
|
|
… |
|
|
|
pk |
теоретические вероят. |
|
|
|||||||
|
|
|
|
|
|
|
|
вероятностей μj (j = |
|
) |
|
||||||||||||||||||
|
Оценка |
отклонения |
эмпирических |
|
1, k |
от |
|||||||||||||||||||||||
теоретических вероятностей p j |
(j = |
|
) |
|
|
||||||||||||||||||||||||
1, k |
производится с помощью критерия |
||||||||||||||||||||||||||||
Пирсона χ2 : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
χнабл2 |
|
|
|
|
(μj |
|
|
− p j ) |
|
N |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
. = ∑ |
|
|
|
. |
|
(1.14) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
p j |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
j=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
По |
таблице |
критических |
точек распределения χ2 (приложения 4) по |
|||||||||||||||||||||||||
заданному уровню значимости |
α и числу степеней свободы r = k −3 ( k - |
||||||||||||||||||||||||||||
количество подынтервалов) находим критическое значение χкр2 (α, r) |
|||||||||||||||||||||||||||||
правосторонней критической области. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
Правило 1.1. Если χнабл2 |
. < χкр2 |
. , тогда нет оснований отвергать гипотезу |
||||||||||||||||||||||||||
H0 о нормальном законе распределения генеральной совокупности (то есть |
|||||||||||||||||||||||||||||
эмпирические и теоретические частоты различаются незначимо (случайно)). |
|
|
|||||||||||||||||||||||||||
|
Правило 1.2. Если χнабл2 |
. > χкр2 |
., тогда гипотеза H0 отвергается. |
|
|
||||||||||||||||||||||||
1.5 СТАТИСТИЧЕСКАЯ И КОРРЕЛЯЦИОННАЯ ЗАВИСИМОСТИ. ЭМПИРИЧЕСКАЯ И ТЕОРЕТИЧЕСКАЯ ЛИНИИ РЕГРЕССИИ
Две случайные величины могут быть связаны между собой функциональной зависимостью, либо зависимостью другого рода, называемой статистической, либо быть независимыми. Строгая функциональная зависимость для случайных величин реализуется редко, так как обе величины (или одна из них) подвержены различным случайным факторам.
12

ПРИМЕР 1.4. Рассмотрим две таблицы значений, которые принимают случайные величины Xи Y.
Таблица 1.6
X |
1 |
7 |
13 |
19 |
25 |
31 |
37 |
Y |
15 |
3 |
25 |
2 |
10 |
16 |
8 |
Таблица 1.7
X |
1 |
7 |
13 |
19 |
25 |
31 |
37 |
Y |
20 |
12 |
15 |
9 |
9 |
3 |
0 |
Изобразим эти данные в декартовой системе координат, откладывая
значения случайной величины X по оси OX , а значения случайной величины Y по оси OY .
y |
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
30 |
|
|
|
|
|
|
|
|
30 |
|
|
|
|
|
|
|
|
25 |
|
|
|
|
|
|
|
|
25 |
|
|
|
|
|
|
|
|
20 |
|
|
|
|
|
|
|
|
20 |
|
|
|
|
|
|
|
|
15 |
|
|
|
|
|
|
|
|
15 |
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
x |
0 |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
0 |
5 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
0 |
5 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
|
|
|
|
Рис.1.1 |
|
|
|
|
|
|
|
|
Рис.1.2 |
|
|
|
|
Данные табл.1.6 представлены на рис.1.1, данные табл. 1.7 – на рис.1.2. Из рис.1.1 видно, что данные табл.1.6 не связаны между собой. А вот из рис.1.2 просматривается какая-то зависимость между X и Y, причем выражена обратная зависимость: с увеличением значений случайной величины X, значения случайной величины Y уменьшаются.
Статистической называют зависимость, при которой изменение одной из величин влечет изменение распределения другой. Если при изменении одной из величин изменяется среднее значение другой, то в этом случае статистическую зависимость называют корреляционной. Значит, корреляционная зависимость есть частный случай статистической зависимости.
Чтобы установить наличие и характер связи между двумя случайными величинами X и Y, нужно привести к удобному виду исходный цифровой материал. Наглядной (удобной) формой представления данных является корреляционная таблица.
|
|
|
|
|
|
|
Таблица 1.8 |
||
Y |
y1 |
y2 |
… |
y j |
… |
yl |
|
mx |
|
X |
|
|
|
|
|
|
|
|
|
x1 |
m11 |
m12 |
… |
m1 j |
… |
m1l |
|
mx 1 |
|
x 2 |
m21 |
m2 2 |
… |
m2 j |
… |
m2 l |
|
mx 2 |
|
… |
… |
… |
… |
… |
… |
… |
|
… |
|
13
xi |
|
mi1 |
mi 2 |
… |
|
mi j |
|
… |
|
mi l |
mxi |
|
|||
… |
|
… |
… |
… |
|
… |
|
|
… |
|
… |
|
… |
|
|
x k |
|
mk1 |
mk 2 |
… |
|
mk j |
|
… |
|
mk l |
mxk |
|
|||
my |
|
my |
my |
2 |
… |
|
my |
j |
|
… |
|
my |
l |
m |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||
Здесь |
x1 , x 2 ,..., x k ; |
y1 , y2 ,..., yl - |
середины подынтервалов |
||||||||||||
сгруппированных |
выборок |
X и |
Y (см. 1.2); |
mi j |
- частота, |
с которой |
|||||||||
встречается пара (xi ; y j ). В последнем столбце и в последней строке таблицы помещены суммарные частоты, соответствующие значению X = xi , и соответственно Y = yi , то есть
mxi = mi1 + mi2 +... + mil ;
my j = m1j + m2 j +... + mkj , тогда должно быть
k
mx1 + mx2 +... + mxk = ∑mxi = m и
i=1
l
my1 + my2 +... + myl = ∑my j = m.
i=1
m - общее количество пар значений (xi ; y j ).
Каждая i −я строка табл. 1.8 представляет собой (совместно с первой строкой) некоторое распределение случайной величины Y, соответствующее
данному значению случайной величины X = xi . Такое распределение
называется условным распределением. Последняя строка табл.1.8 совместно с первой строкой образует безусловное распределение случайной величины Y (ее эмпирический закон распределения):
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 1.9 |
|
Y |
y1 |
y2 |
… |
y j |
|
… |
yl |
|
|
||
|
my |
my |
my |
2 |
… |
my |
j |
… |
my |
l |
|
|
|
|
1 |
|
|
|
|
|
|
|
|||
Каждый j −й столбец табл.1.8 представляет собой совместно с первым |
||||||||||||
столбцом некоторое распределение случайной величины X, |
соответствующее |
|||||||||||
данному значению |
случайной |
величины |
Y = y j |
(то |
|
есть условное |
||||||
распределение). Последний столбец табл. 1.8 совместно с первым столбцом образует безусловное распределение случайной величины X (ее эмпирический закон распределения):
Таблица 1.10
X |
x1 |
x 2 |
… |
xi |
|
… |
x k |
||
mx |
mx |
mx |
2 |
… |
mx |
i |
… |
mx |
k |
|
1 |
|
|
|
|
|
|||
14

По данным табл. 1.9 и 1.10 вычисляем средние значения:
|
l |
|
X = |
|
k |
|
|
|
m |
|
|
||
Y = ∑y j my m ; |
|
∑xi mx |
|
|
|
||||||||
|
j=1 |
j |
|
i=1 |
|
i |
|
|
|
||||
и средние квадратические отклонения: |
|
|
|
|
|
|
|
|
|||||
2 l |
|
|
2 |
|
2 |
k |
|
|
2 |
mx |
|
m . |
|
|
|
|
|||||||||||
σY = ∑ |
(y j − Y) |
my m σX = ∑ |
(xi − X) |
|
|||||||||
j=1 |
|
|
|
j |
i=1 |
|
|
|
|
i |
|
|
|
(1.15)
(1.16)
Замечание 1.3. Рекомендуется сделать два рисунка – это графические изображения эмпирических законов распределения случайных величин X и Y
в виде распределения частот. На рисунках нанести средние значения X и Y . Уточним определение корреляционной зависимости. Для этого введем
понятие условной средней. Для каждой i -й строки табл.1.8 (совместно с первой строкой) можно вычислить среднее значение случайной величины Y (по
формуле 1.15), которое называется условным средним: |
|||||||||||
|
|
xi = |
|
|
(X = xi ) |
(i =1, 2,..., k). |
|||||
|
Y |
Y |
|||||||||
Так как каждому значению xi соответствует одно значение условной |
|||||||||||
средней, то, очевидно, условная средняя |
|
xi |
есть функция от X. В этом случае |
||||||||
Y |
|||||||||||
говорят, что случайная величина Y зависит от X корреляционно. |
|||||||||||
Корреляционной зависимостью Y от X называют функциональную |
|||||||||||
зависимость условной средней |
|
|
x от X: |
|
|||||||
Y |
|
||||||||||
|
|
|
|
x = f (X). |
(1.17) |
||||||
|
|
|
Y |
||||||||
Уравнение (1.17) называется уравнением регрессии Y на X; функция называется регрессией Y на X; график функции f (X) - линией
регрессии Y на X. |
|
||||||||
Аналогично для каждого j −го столбца табл.1.8 |
(совместно с первым |
||||||||
столбцом) можно вычислить среднее значение случайной величины X по |
|||||||||
формуле (1.15), которое называется условным средним: |
|
||||||||
|
|
y j = |
|
(Y = y j ) (j =1, 2,..., l). |
|||||
|
X |
X |
|||||||
Тогда корреляционной зависимостью X от Y называется |
|||||||||
функциональная зависимость |
|
|
y от Y: |
|
|||||
X |
|
||||||||
|
|
|
|
y = ϕ(Y). |
|
||||
|
|
|
X |
(1.18) |
|||||
15

Уравнение (1.18) называется уравнением регрессии X на Y; функция ϕ(Y) называется регрессией X на Y; график функции ϕ(Y) - линией
регрессии X на Y.
Замечание 1.4. Рассматриваемые два уравнения регрессии существенно различны и не могут быть получены одно из другого.
Изучение корреляционной связи будем проводить при решении двух основных задач:
-определение формы корреляционной связи, то есть вида теоретической функции регрессии (она может быть линейной и нелинейной);
-определение тесноты (силы) корреляционной связи.
Наиболее простой и важный случай корреляционной зависимости - линейная регрессия. В этом случае теоретическое уравнение линейной
регрессии Y на X (формула 1.17) имеет вид |
|
Yx = aX + b . |
(1.19) |
Коэффициент a в уравнении (1.19) называют коэффициентом регрессии Y на X и обозначают ρYX (a = ρYX ). Оценки неизвестных параметров ρYX и
b рассчитаем, применяя данные табл.1.8:
|
k |
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y |
|
||||||||
|
∑∑mij xi y j m − X |
|
||||||||||||
a = ρYX = |
i=1 j=1 |
|
|
|
|
|
|
. |
(1.20) |
|||||
|
k |
2 |
|
|
|
|
2 |
|
||||||
|
|
|
|
|
|
|
|
|
||||||
|
|
∑xi |
mx |
m −(X) |
|
|
|
|
|
|||||
|
|
i=1 |
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b = |
|
−ρYX |
|
, |
(1.21) |
|||
|
|
|
Y |
X |
|||||||||
где |
|
и |
|
|
- средние значения случайных величин |
|
и |
|
, |
||||
X |
|
Y |
X |
Y |
|||||||||
вычисленные по формулам (1.15). |
|
|
|
|
|||||||||
Сделаем графическое изображение так называемой эмпирической линии |
|||||||||||||
регрессии Y на |
X и теоретической линии регрессии Y на X. Для этого в |
||||||||||||
декартовой системе координат по оси OX откладываем значения x1 , x 2 ,..., x k из табл. 1.8, по оси OY откладываем значения условных средних Yxi . Тогда
ломаная, соединяющая точки (x1 , |
|
x |
); |
(x 2 , |
|
x |
); … ; |
(x k , |
|
x |
), и будет |
||
Y |
Y |
Y |
|||||||||||
1 |
|
|
|
2 |
|
|
|
|
|
k |
|||
эмпирической линией регрессии Y на |
X. Здесь же на данном графике строим |
||||||||||||
теоретическую линию регрессии, |
то |
есть прямую |
|
|
x = ρYX X + b с |
||||||||
|
Y |
||||||||||||
вычисленными коэффициентами.
Замечание 1.5. Поскольку формулы (1.20) и (1.21) получены по методу наименьших квадратов, то по сути этого метода, теоретическая линия регрессии должна на графике быть в «середине» ломаной.
16

Аналогично можно поставить вопрос о нахождении теоретического уравнения линейной регрессии X на Y (формула 1.18), которое в этом случае имеет вид
|
|
|
|
y = a1Y + b1 . |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
X |
|
|
|
|
|
|
|
|
|
(1.22) |
||||||
Коэффициент a1 в уравнении (1.22) называют коэффициентом |
|||||||||||||||||||
регрессии X на Y и обозначают |
ρXY (a1 = ρXY ). Оценки |
неизвестных |
|||||||||||||||||
параметров ρXY и b1 рассчитываются по данным табл.1.8: |
|
||||||||||||||||||
|
|
|
k l |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
Y |
|
|||||||||||
|
|
∑∑mij xi y j |
m − X |
|
|||||||||||||||
a1 |
= ρXY = |
i=1 j=1 |
|
|
|
|
|
|
. |
(1.23) |
|||||||||
|
l |
|
|
|
|
|
|
2 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
∑y2j my |
|
|
m −(Y) |
|
|
|
|
|||||||||
|
|
|
j=1 |
|
j |
|
|
|
|
|
|
|
|
|
|
||||
|
|
b1 = |
|
−ρXY |
|
, |
|
|
|
(1.24) |
|||||||||
|
|
X |
Y |
|
|
|
|||||||||||||
где X и Y средние значения случайных величин X и Y, вычисленные по формулам (1.15).
Далее целесообразно сделать графическое изображение эмпирической и теоретической линий регрессии X на Y аналогично вышеизложенному.
Вслучае линейной регрессии задача определения тесноты связи сводится
квычислению эмпирического (выборочного) коэффициента корреляции, который можно вычислить по одной из формул:
r |
= ρ |
YX |
|
σX |
или |
r = ρ |
XY |
|
σY |
, |
(1.25) |
||
|
|
||||||||||||
В |
|
σ |
Y |
|
В |
|
σ |
X |
|
||||
|
|
|
|
|
|
|
|
|
|
||||
где σX , |
σY |
|
|
|
|
|
|
|
|
|
|
||
- значения |
средних |
квадратических |
отклонений, |
||||||||||
вычисленных по формуле (1.16).
Приведем свойства выборочного коэффициента корреляции: 1. rВ <1 или −1 ≤ rВ ≤1.
2. Если rВ = 0, тогда X и Y не связаны линейной корреляционной
зависимостью (но могут быть связаны нелинейной корреляционной или даже функциональной зависимостью).
3. С возрастанием абсолютной величины выборочного коэффициента корреляции линейная корреляционная зависимость становится более тесной и
при |
|
rВ |
|
|
=1 переходит в линейную функциональную зависимость. |
|
|
||||
4. |
Если rВ =1 (rВ = −1), тогда X и Y связаны прямой (обратной) |
||||
линейной функциональной зависимостью.
17
