Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Уфимский Государственный Нефтяной Технический Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

razdel3UMK

.pdf

Скачиваний:

Добавлен:

17.03.2015

Размер:

1.22 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 78 / 148 9 10 11 12 13 14 > Следующая >>>

ПРИМЕР 2.25. Построить кривую, заданную в параметрическом виде

x = cos ty = sin t .

Решение.

1) t R , x = x(t) и y = y(t) периодические с периодом равным 2π, по-

этому достаточно рассмотреть t [0; 2π]; 2) −1 ≤ x ≤1,

3) −1 ≤ y ≤1;

	π
t =	2
4) а) пересечение с осью Oy : x = 0 , тогда cos t = 0;	2	π	, следова-
4) а) пересечение с осью Oy : x = 0 , тогда cos t = 0;			, следова-

t = −		2
		2

тельно

y =1

;

точки пересечения с осью

Oy - (0;1); (0; −1);

= −1

б)

пересечение с осью

Ox :

y = 0

, тогда

sin t = 0;

t = 0

, следова-

= π

тельно

x =1

; точки пересечения с осью Ox - (1;0); (−1;0);

= −1

5) рассматриваем t [0; 2π], поэтому не исследуем при t → ∞.

Составим таблицу

2π

3π

5π

−1

−

− 2

−

t		7π			5π	4π		3π		5π			7π	11π

		6			4	3		2	3			4		6
		6			4	3		2	3			4		6

x	−	3		−	2	−	1	0			1	2		3
x	−	3		−	2	−		0	2			2		3
		2			2	2			2			2		2
y			1		2	3			3			2				1
y	− 2			− 2		− 2		−1	− 2			− 2			− 2
	− 2			− 2		− 2		−1	− 2			− 2			− 2

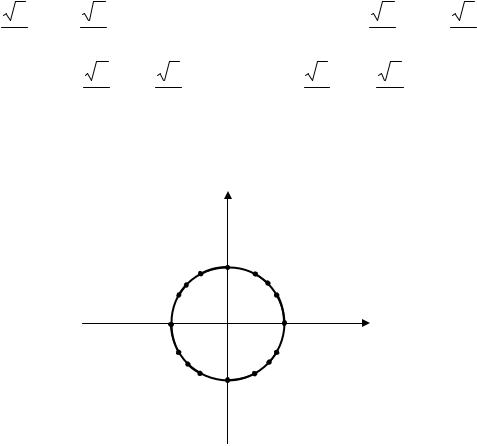
Нанесем полученные точки на плоскость xOy . y

-1

Графиком является окружность. Действительно,

x 2 + y2 = cos2 t + sin 2 t =1;

уравнение окружности

x 2 + y2 =1.

2.6.ПРЕДЕЛ ЧИСЛОВОЙ ПОСЛЕДОВАТЕЛЬНОСТИ

2.6.1.Числовые последовательности

Числовые последовательности встречаются уже в программе средней школы. Примерами таких последовательностей являются: 1) последовательность членов арифметической и геометрической прогрессий; 2) последовательность периметров правильных n − угольников, вписанных в данную окружность.

Уточним и расширим понятие числовой последовательности.

Пусть каждому натуральному числу n поставлено в соответствие действительное число xn . Тогда говорят, что задана последовательность чисел

x1 ,x2 ,K,xn ,K .

(2.1)

Числа x1 , x2 ,K, xn будем называть элементами (или членами) после-

довательности, xn − общим членом последовательности. Сокращенно по-

следовательность (2.1) будем обозначать символом {xn }. Так, например, сим-

	1		1,	1	,	1	,K,	1	,K. Зная формулу об-
вол		обозначает последовательность
				2		3		n
n

щего члена последовательности, можно записать любой член этой последовательности.

ПРИМЕР 2.26. Дан общий член последовательности: xn = n n+1. Напи-

сать пять первых членов последовательности.

Решение. Положив последовательно n = 1,2,3,4,5 в общем члене xn

получаем x1 = 12 ,x2 = 23 ,x3 = 43 ,x4 = 45 ,x5 = 56 .

ПРИМЕР 2.27. Задана числовая последовательность: 1, 312 , 512 , 712 ,K.

Написать формулу общего члена.

Решение. Знаменатель членов данной последовательности образуют последовательность всех нечетных натуральных чисел в степени 2 . Поэтому

xn = 1 2 . (2n −1)

2.6.2. Ограниченные и неограниченные последовательности

ОПРЕДЕЛЕНИЕ 2.1. Последовательность {xn } называется ограни-

ченной сверху (снизу), если существует число M (число m) такое, что любой элемент xn этой последовательности удовлетворяет неравенству

xn ≤ M (xn ≥ m).

ОПРЕДЕЛЕНИЕ 2.2. Последовательность {xn } называется ограни-

ченной, если она ограничена и сверху и снизу, т.е. существуют числа m и M такие, что любой элемент этой последовательности удовлетворяет неравенствам

m ≤xn ≤M

Обозначим A = max{ m , M }. Тогда условие ограниченности последовательности можно записать в виде xn ≤ A или − A ≤ xn ≤ A .

ОПРЕДЕЛЕНИЕ 2.3. Последовательность {xn } называется неограниченной, если для любого положительного числа A существует элемент xn этой последовательности, удовлетворяющей неравенству xn > A .

Из данных определений следует, что если последовательность ограничена сверху, то все ее элементы принадлежат промежутку (− ∞; M], а сели последо-

вательность ограничена снизу - промежутку [m;+∞), а в случае ограниченности и сверху и снизу - промежутку [m; M]. Неограниченная последователь-

ность может быть ограничена сверху или снизу. Рассмотрим несколько примеров.

1.Последовательность {n}, или, что то же, 1,2,3,K, n,K, ограничена снизу (m = 1), но не ограничена сверху.

2.Последовательность {− n}, или, что то же −1, − 2,− 3,K, − n,K,, ограничена сверху (M = −1), но не ограничена снизу.

	1		1		1		1
3. Последовательность		, или, что то же, 1,		,		,K,		,K, ограниче-
			2		3		n
n

на, так как любой элемент xn	этой последовательности удовлетворяет неравен-
ствам 0 ≤ xn ≤1 (m = 0,M =1).
4. Последовательность	{(−1)n n} или,	что то же, −1, 2, − 3,4,
K,(−1)n n,K− неограниченная. В самом деле,		каково бы ни было число A ,

среди элементов xn этой последовательности найдутся элементы, для которых будет выполняться неравенство xn > A .

2.6.3. Предел числовой последовательности

ОПРЕДЕЛЕНИЕ 2.4. Число a называется пределом числовой последо-

вательности {xn }, если для любого сколь угодно малого ε > 0 найдется число N , зависящее от ε , такое, что для всех натуральных чисел n > N выполняется неравенство xn − a < ε.

При этом последовательность

{xn }

называется сходящейся и в этом

случае пишут

lim xn

= a .

n→∞

ПРИМЕР

2.28.

Используя

определение предела, показать,

что

lim

= 1.

n→∞ n +1

Решение.

Возьмем любое число ε > 0.

Так как

xn −1

−1

n +

n ,

то для нахождения значений

удовлетворяющих неравенству

n +1

xn −1

< ε, достаточно решить неравенство

< ε, откуда получим

n >

1− ε

1 − ε

. Следовательно, за N можно взять целую часть числа

т.е.

1−ε

N(ε)=

. Тогда неравенство

−1

< ε

будет выполняться при всех


n > N . Так как ε − любое, то доказано, что lim			n		= 1.
n > N . Так как ε − любое, то доказано, что lim					= 1.
		n→∞ n +1
Для более четкого понимания определения предела проверим проведен-
ные вычисления на конкретных числах.
		1 − 0,01
Пусть, например, ε = 0,01. Тогда N =				= 99 и при		n > N
Пусть, например, ε = 0,01. Тогда N =				= 99 и при		n > N
		0,01
имеем	xn −1	< 0,01. В частности, при n < N (n = 97, n = 98) данное не-
имеем	xn −1	< 0,01. В частности, при n < N (n = 97, n = 98) данное не-

равенство не выполняется. (Убедиться в этом самостоятельно). Если же взять

значение ε = 0,001, то

значение номера

N увеличивается. В самом деле,

N =

1 − 0,001

= 999 и при n > N = 999 получаем

xn −1

< 0,001.

0,001

2.29. Пусть x1 = 0,9,

= 0,99, x3

= 0,999, K. Показать,

ПРИМЕР

что предел этой последовательности равен 1.

Решение. Имеем

xn = 1 −

(n = 1,2,3,K).

Возьмем произвольное

10n

ε > 0. Тогда

−1

и неравенство

xn −1

< ε будет выполняться для

10n

всех значений n , удовлетворяющих условию

< ε. Отсюда n > lg

, сле-

10n

довательно N(ε)= lg

а значит lim x

= 1.

n→∞

) зависит от

Из рассмотренных примеров видно, что число

2.7.ПРЕДЕЛ ФУНКЦИИ

2.7.1.Предел функции при x → x0

Пусть функция y = f(x) определена в некоторой окрестности точки x0 , в самой же точке x0 функция может быть даже и не определена.

ОПРЕДЕЛЕНИЕ 2.5. Число A называется пределом функции f(x) в

точке x = x0 (или при x → x0 ), если для любого сколь угодно малого ε > 0
найдется число δ > 0 (зависящее от ε ) такое, что для всех x ,					удовлетворяю-
щих неравенству			x − x0	< δ (x ≠ x0 ), выполняется	неравенство
щих неравенству			x − x0	< δ (x ≠ x0 ), выполняется	неравенство
	f(x)− A	< ε. В этом случае пишут lim f(x) = A.
	f(x)− A	< ε. В этом случае пишут lim f(x) = A.
				x→x0
				x→x0

ПРИМЕР 2.30. Используя определение предела, доказать, что функция

f(x) = 3x − 2 в точке x = 1 имеет предел, равный 1, т.е. lim(3x − 2) = 1.

x→1

Решение. Возьмем любое ε > 0. Задача состоит в том, чтобы по заданному ε найти такое положительное число δ = δ(ε), при котором из неравенства

x −1

< δ

следовало бы неравенство

f(x)−1

(3x − 2)−1

< ε. Преобра-

зуя последнее неравенство, получаем

3(x −1)

< ε, или

x −1

< ε .

Отсюда видно, что если за δ = δ(ε) принять любое число не превосхо-

дящее ε,

т.е. положить δ ≤ ε , то для всех x ,

удовлетворяющих неравенству

f(x)−1

x −1

< δ, выполняется требуемое неравенство

< ε. Это и означает,

что

lim(3x − 2) = 1. В частности, если ε = 1, то δ ≤

; если ε = 0,5

то

x→1

δ ≤

; если ε = 0,03, то δ ≤ 0,01 и т.д. Таким образом,

δ зависит от ε,

по-

этому в определении предела иногда пишут δ = δ(ε).

ПРИМЕР 2.31. Используя определение предела, доказать, что функция

f(x) = x sin

определенная для всех

x ≠ 0, в точке x = 0 имеет предел,

равный 0, т.е. lim x sin

= 0.

x→0

Решение.

Возьмем любое ε > 0. Как и ранее, по этому ε надо найти та-

кое δ > 0, при котором из неравенства

x − 0

< δ следовало бы неравенство

f(x)− 0

x sin

− 0

x sin

< ε.

Из

последнего неравенства имеем

x sin

− 0

sin

≤

< ε

sin

≤ 1 при x ≠ 0 . Отсюда видно,

что если взять

δ ≤ ε,

то,

как

только

< δ, справедливо неравенство

x sin

< ε. Следовательно,

lim x sin

x→0

2.7.2. Предел функции при x → ∞

ОПРЕДЕЛЕНИЕ 2.6. Число A называется пределом функции f(x) при

x → ∞, если для любого сколь угодно малого ε > 0 найдется число M > 0
такое, что для всех значений x , удовлетворяющих неравенству			(		x	> M , вы-
					x	> M , вы-
полняется неравенство	f(x)− A	< ε. В этом случае пишут lim f		x) = A .
полняется неравенство	f(x)− A	< ε. В этом случае пишут lim f		x) = A .
		x→∞
		x→∞
ОПРЕДЕЛЕНИЕ 2.7. Число A называется пределом функции f(x) при

x → +∞, если для любого сколь угодно малого ε > 0 найдется число M > 0 такое, что для всех значений x , удовлетворяющих неравенству x > M , выпол-

няется неравенство f(x)− A < ε.

Аналогичным образом формулируется определение предела функции при

x → −∞

. Рекомендуем это сделать самостоятельно.

ПРИМЕР 2.32.

Используя

определение предела доказать, что

lim

x +1

x→∞ 2x +1

x +1

Решение. Равенство

lim

означает, что для любого ε > 0 су-

2x +1

M > 0 такое,

x→∞

> M следует неравенство

ществует

что

из неравенства

x +1

−

< ε

или

2x +1

. Найдем значения x , для которых

2x +1

≥

−1, то достаточно

выполняется последнее неравенство.

Так как

−1 >

решить неравенство

, откуда получаем

. Если взять

M =

> M , будет

, то для всех

x ,

удовлетворяющих неравенству

выполняться неравенство

x +1

−

< ε, а это означает, что lim

x +1

2x +1 2

5x +1

x→∞ 2x +1

ПРИМЕР 2.33.

Доказать, что

lim

3x + 9

x→+∞

Решение.

Данное равенство означает, что для любого ε > 0 существует

5x +1

M > 0 такое, что из неравенства x > M следует неравенство

−

3x + 9

< ε. Так как x > 0,

то последнее неравенство равносильно неравен-

3x + 9

ству

< ε, отсюда получаем x >

14 − 9ε

. Если положить M =

14 − 9ε

3x + 9

3ε

то для всех x , удовлетворяющих неравенству x

M , будет выполняться нера-

венство

5x +1

−

< ε. А это означает, что lim

5x +1

3x + 9

x→+∞

2.7.3. Односторонние пределы

ОПРЕДЕЛЕНИЕ 2.8. Пусть переменная x стремится к x0 , оставаясь

меньше, чем x0 (x < x0 ). Если при этом функция f(x) стремится к некоторо-

му пределу A ,

то этот предел называют пределом функции f(x) в точке x0

слева и записывают

lim

f (x)= А. Если же переменная x стремится к x0 ,

x→x0 −0

оставаясь больше x0 (x > x0 ), и при этом функция f(x)

стремится к пределу

B, то этот предел называют пределом функции f(x) в этой точке x0

справа

и записывают

lim

f(x) = B.

x→x0 +0

Пределы функции f(x)

в точке

слева

и справа называют односто-

ронними пределами.

Для

чисел

A и

иногда

употребляется символическая

запись

A = f(x0 − 0), B = f(x0 + 0).

Для существования предела функции f(x)

при

x → x0

необходимо и

достаточно выполнения равенства

lim f (x)=

lim f (x).

В этом

случае

x→x0 −0

x→x0

предел функции равен односторонним пределам.

x −1

ПРИМЕР 2.34. Найти односторонние пределы функции

f(x) =

x −1

точке x = 1.

При x → 1 − 0 имеем x < 1 или x −1 < 0,

Решение.

следовательно

lim

x −1

= lim

x −1

= −1.

Аналогично,

при

x → 1 + 0 имеем

x > 1

x −1

−(x −1)

x→1−0

или x −1 > 0,

поэтому lim

x −1

= lim

x −1

= 1.

Функция в точке

x = 1

x −1

x→1+0

x→1+0 x −1

имеет левый и правый пределы, но они не равны. Это означает, что данная

функция в точке x =

1 предела не имеет.

при x < 0,

ПРИМЕР 2.35.

Доказать, что функция f(x) = x

в точке

x = 0 имеет предел.

при x > 0

Решение. Функция f(x) определена на всей числовой прямой, кроме точ-

ки

x = 0.

Вычислим

этой

точке

односторонние пределы.

Имеем

lim f(x) = lim x = 0;

lim f(x) = lim x2

= 0.

Следовательно, в

точке

x→0−

x→0+

x =

0 данная функция имеет правый и левый пределы и они равны. Это озна-

чает, что данная функция в точке

x = 0 имеет предел и он равен нулю, т.е.

lim f (x)= lim f (x)

= lim f (x)

= 0.

x→0−

x→0+

x→0

2.7.4. Бесконечно большие и бесконечно малые функции

ОПРЕДЕЛЕНИЕ 2.9. Функция f(x) называется бесконечно большой

при

x → x0 , если

для

любого

M > 0 существует δ > 0 такое,

что для

всех

x − x0

< δ, x ≠ x0 , выполняется неравенство

f(x)

> M . В этом случае

пишут lim f(x) = ∞.

x→x0

x → ∞,

Аналогично определяются бесконечно большие функции при

x → +∞ и

x → −∞.

Так,

например, функция

f(x) называется бесконечно

большой			при x → ∞, если для любого M > 0 существует δ > 0 такое, что для
всех x ,			удовлетворяющих неравенству	x	> δ выполняется неравенство
всех x ,			удовлетворяющих неравенству	x	> δ выполняется неравенство
	f(x)	> M . При этом пишут lim f(x) = ∞.
	f(x)	> M . При этом пишут lim f(x) = ∞.
			x→∞
			x→∞

Предлагаем самостоятельно сформулировать определение бесконечно большой функции при x → +∞ и x → −∞.

ПРИМЕР 2.36. Доказать, что функция f(x) =

при x → 1 является

x −1

бесконечно большой, т.е.

lim

= ∞.

x −1

x→1

Решение. Согласно определению надо доказать, что для любого M > 0 суще-

ствует δ > 0 такое,

что

из

неравенства

x −1

< δ

следует

неравенство

f(x)

> M , т.е.

> M .

Возьмем любое M > 0 и

решим

неравенство

x −

> M . Отсюда

x −1

. Таким образом,

в качестве δ

можно взять

x −1

число M1 . Это и означает, что данная функция является бесконечно большой при x → 1.

ОПРЕДЕЛЕНИЕ 2.10. Функция f(x) называется бесконечно малой при

x → x0 , если lim f(x) = 0.

x→x0

Аналогично определяются бесконечно малые функции при x → ∞,

x → +∞ и x → −∞.

Используя определение предела функции, можно дать другое равносильное определение бесконечно малой функции “на языке ε −δ”: функция f(x)

называется бесконечно малой при x → x0 , если для любого ε > 0 сущест-
вует		δ > 0		такое, что для всех x, удовлетворяющих неравенству
	x − x0		< δ,	x ≠ x0 , выполняется неравенство	f(x)	< ε.

Основные свойства бесконечно малых функций, которые используются на практике, содержатся в следующей теореме:

Теорема 2.1. Алгебраическая сумма и произведение конечного числа бесконечно малых функций при x → x0 , а также произведение бесконечно малой функции на ограниченную функцию являются бесконечно малыми функ-

циями при x → x0 .
Все сказанное о бесконечно малых функциях при x → x0 справедливо и
для бесконечно малых функций при x → ∞ , x → +∞, x → −∞.
ПРИМЕР 2.37. Доказать, что функция f(x)	= (x +1)sin			1	при
ПРИМЕР 2.37. Доказать, что функция f(x)	= (x +1)sin			x +1	при
		1		x +1
x → −1 является бесконечно малой, т.е. lim (x +1)sin		1	= 0.
x → −1 является бесконечно малой, т.е. lim (x +1)sin		x +1	= 0.
x→−1		x +1

<<< < Предыдущая 1 2 3 4 5 6 78 / 148 9 10 11 12 13 14 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
17.03.20151.15 Mб48razdel1kim.pdf
#
17.03.20151.31 Mб24razdel1UMK.pdf
#
17.03.20151 Mб59razdel2kim.pdf
#
17.03.20151.08 Mб32razdel2UMK.pdf
#
17.03.2015780.33 Кб33razdel3kim.pdf
#
17.03.20151.22 Mб87razdel3UMK.pdf
#
17.03.2015768.02 Кб25razdel4kim.pdf
#
17.03.20151.03 Mб39razdel4UMK.pdf
#
17.03.201569.38 Кб33rechev_kommun.docx
#
26.11.201874.24 Кб6ref-23736.doc
#
29.07.2019143.87 Кб6Referat Istoria.doc