Используя правило возведения в степень, получим

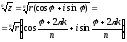, (6.3.4)

где k=0,1,2, …, n-1.

Геометрически эти n значений выражения 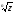изображаются вершинами некоторого правильного n - угольника, вписан­ного в окружность, с центром в -нулевой почке радиуса.

С помощью формулы Эйлера можно привести к более простому виду:

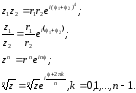
Рассмотрим множества точек на плоскости и дадим некоторые определения.

Определение 6.3.1. Множество точек г комплексной плоскости, удовлетворяющее неравенству 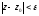, называетсяe - окрестностью точки z₀.

Определение 6.3.2. Точка r называется внутренней точкой множества Е точек комплексной плоскости, если существует e окрестность точки z, целиком принадлежащая множеству Е.

Определение 6.3.3. Множество Е называется областью, если оно обладает следующими свойствами;

1) каждая точка Е является внутренней;

2) любые две точки, принадлежащие Е, можно соединить ломаной, состоящей ив точек множества Е. Второе свойство в этом определении называют свойством связности области.

Определение 6.3.4. Граничной точкой области G называется точка, не принадлежащая самой области, но любая e, окрестность которой содержит точки G.

Например , z=1 является граничной точкой области .

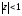Определение 6.3.5. Совокупность всех граничных точек называется границей области G.

Определение 6.3.6. Область с присоединенной к ней границей называется замкнутой областью и обозначается через .

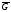Например, замкнутой областью является множество 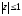Определение 6.3.7. Число связных частей, на которые разбивается область, называется порядком связности области. Например, область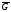- односвязная (рис. 6.3.1.).

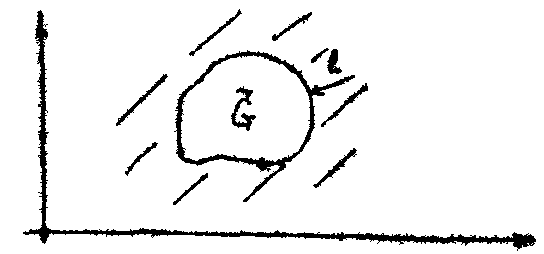
Рис. 6.3.1.

Пусть границей является кривая С. Положительным направлением обхода называется такое направление, при котором обходимая область остается слева.

Определение 6.3.8. Область G называется ограниченной, если она лежит внутри некоторого круга конечного радиуса.

Пример 6.3.1. Решить уравнение z²-6z+10=0.

Решение. В результате подстановки z=x+iy в данное уравнение имеем

(x+iy)²-6(x+iy)+10=0 , откуда после преобразований получим систему уравнений

x²-y²-6x+10=0;

xy-3y=0.

Решая систему, получим z₁=x₁+iy₁=3+I ; z₂=x₂+iy₂=3-I.

Пример 6.3.2. Выяснить геометрический смысл модуля разности |z₁-z₂| двух комплексных чисел z₁ и z_{2 .}

Решение. |z₁-z₂ |= | (x₁-x₂)+i(y₁-y₂)|=.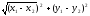

Следовательно, |z₁-z₂ | означает расстояние между точками z₁=x₁+iy₁ и z₂=x₂+iy₂

Если изобразить комплексное число с помощью вектора, то действительная и мнимая части z₁-z₂ являются координатами вектора, а так как при вычислении векторов координаты соответственно вычитаются, то вычитание комплексных чисел сводится к вычитанию векторов, изображающих эти числа

Как видно из рис.1а, | z₁-z₂ | есть длина вектора z₁-z₂=М₂М_1, иначе расстояние между точками ,

Пример 6.3.3. Выяснить, какой геометрический смысл имеет модуль разности двух комплексных чисел.

Решение.

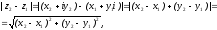
то есть 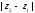равен расстоянию между точками.

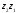6.4.Дифференциальные уравнения Основные понятия

Определение 6.4.1.Уравнение, связывающее независимую переменную, неизвестную функцию и ее производные или дифференциалы различных порядков, называется обыкновенным дифференциальным уравнением.

Определение 6.4.2. Порядком дифференциального уравнения называется порядок старшей производной, входящей в данное уравнение.

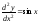Например, уравнение - первого порядка;- второго порядка;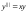- третьего порядка и т. д.

Решением дифференциального уравнения называется функция y=y(x), удовлетворяющая этому уравнению. График решения на плоскости xOy называется интегралом уравнения.

Процесс нахождения решения называется интегрированием дифференциального уравнения.

Если решение уравнения получено в неявном виде 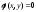, то оно обычно называетсяинтегралом уравнения.

Задача Коши для уравнения

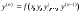(6.4.1)

ставится следующим образом. Среди всех решений уравнения (6.4.1) требуется найти решение y=y(x), для которого функция y(x) вместе со своими производными до (n-1)-го порядка включительно принимает заданные значения 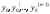при заданном значенииx₀ аргумента x, т.е.

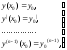(6.4.2)

где x₀, y₀, y₀^|,…,y₀^(n-1) – заданные числа.

Условия (6.4.2) называются начальными условиями решения y=y(x), а само это решение – частным решением уравнения (6.4.1), удовлетворяющим начальным условиям (6.4.2).

Общее решение уравнения (6.4.1) – это решение вида 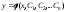, зависящее отn произвольных постоянных C₁, C₂, …C_n, которые можно подобрать таким образом, чтобы удовлетворить любой системе начальных условий.

Частное решение уравнения (6.4.1) может быть получено из общего решения при некоторых числовых значениях произвольных постоянных C₁, C₂, …C_n.