
- •Понятие дифференциала. Геометрический смысл дифференциала. Инвариантность формы первого дифференциала.
- •Производные и дифференциалы высших порядков
- •Производная параметрически и неявно заданных функций
- •Дифференцирование функций, заданных параметрически
- •Определения
- •Теорема Ролля
- •Теорема Лагранжа
- •Тейлора многочлен
Определения
Пусть
дана функция ![]() и
и ![]() —
внутренняя точка области определения f. Тогда
—
внутренняя точка области определения f. Тогда
x0 называется точкой локального максимума функции f, если существует проколотая окрестность
 такая,
что
такая,
что
![]()
x0 называется точкой локального минимума функции f, если существует проколотая окрестность
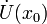 такая,
что
такая,
что
![]()
Если неравенства выше строгие, то x0 называется точкой строгого локального максимума или минимума соответственно.
x0 называется точкой абсолютного (глобального) максимума, если
![]()
x0 называется точкой абсолютного минимума, если
![]()
Значение функции f(x0) называют (строгим) (локальным) максимумом или минимумом в зависимости от ситуации. Точки, являющиеся точками (локального) максимума или минимума, называются точками (локального) экстремума.
великая теорема Ферма, знаменитая теорема Ферма, большая теорема Ферма, последняя теорема Ферма,- утверждение, что для любого натурального числа п>2 уравнение xn+yn=zn (уравнение Ферма) не имеет решений в целых ненулевых числах х, у, z.
Ферма малая теорема, одна из основных теорем теории чисел, состоящая в том, что если р – простое число и а –целое число, не делящееся на р, то ap-1 – 1 делится на р, т. е. ap-1º1(modp). Теорему высказал без доказательства П.Ферма, первое доказательство дал Л. Эйлер.
45
Теорема Ролля
Пусть функция f (x) непрерывна на [a, b], дифференцируема на (a, b) и на концах отрезка принимает равные значения f(a) = f(b). Тогда существует точка c (a, b), в которой f ' (c) = 0. Доказательство. Так как функция f(x) непрерывна на [a, b],то по свойству непрерывных функций она достигает на этом отрезке максимальное значение М и минимальное значение m. Возможны два случая: максимум и минимум достигаются на концах отрезка или что – либо (или максимум, или минимум) попадает вовнутрь интервала. В первом случае f (x) = const = M = m. Поэтому производная равна нулю f ' (c) = 0 в любой точке отрезка [a, b], и теорема доказана. Во втором случае, так как f (x) дифференцируема в точке c, из теоремы Ферма следует, что f ' (c) = 0.
46
Теорема Лагранжа
Если функция f(x) непрерывна на замкнутом отрезке [a, b], дифференцируема внутри него, то существует такая точка с (a, b), что выполняется равенство
f(b) − f(a) = f '(c)·(b − a).
Д о к а з а т е л ь с т в о. Составим уравнение хорды, проходящей через точки (a, f(a)), (b, f(b))
y = f(a) + Q·(x - a),
где ![]() есть
угловой коэффициент хорды. Рассмотрим
разность ординат функции и хорды
есть
угловой коэффициент хорды. Рассмотрим
разность ординат функции и хорды
F(x) = f(x) − f(a) − Q·(x − a).
Очевидно, что функция F(x) удовлетворяет всем условиям теоремы Ролля. Поэтому на интервале (a, b) найдётся такая точка с, для которой F ' (c) = 0. То есть F ' (c) = f ' (c) − Q = 0. Откуда следует
![]() .
.
И, наконец, f(b) − f(a) = f '(c)·(b − a).
47
![]() tg
угла наклона хорды АВ к оси х.
tg
угла наклона хорды АВ к оси х.
![]() tg
угла наклона касательной.
tg
угла наклона касательной.
В
(a,b) найдется по крайней мере одна точка ![]() ,
в которой касательная к графику функции
будет параллельна хорде АВ.
,
в которой касательная к графику функции
будет параллельна хорде АВ.
Следствия:
1.
Если функция f дифференцируема в (a,b)
и ![]() всюду
в этом интервале неотрицательна
(неположительна), то f не убывает (не
возрастает) на этом интервале.
всюду
в этом интервале неотрицательна
(неположительна), то f не убывает (не
возрастает) на этом интервале.
Доказательство:
Если ![]() .
.
Так
как точки ![]() -
произвольные точки, то для отрезка
-
произвольные точки, то для отрезка ![]() и
функции f будут выполняться все условия
теоремы Лагранжа, так как
и
функции f будут выполняться все условия
теоремы Лагранжа, так как ![]() .
.
Тогда ![]() .
.
Если ![]() в
любой точке интервала, то
в
любой точке интервала, то ![]() .
.
![]()
![]()
![]()
![]()
![]()
аналогично,
если ![]() ,
то
,
то ![]() .
.
Доказано.
48
Теорема Коши
Теорема
20.1 (теорема Коши). Пусть функции f(x) и g(x)
непрерывны на отрезке [a;b] и
дифференцируемы во всех внутренних
точках этого отрезка, причём
производная ![]() отлична
от нуля во всех внутренних точках
отрезка [a;b]. Тогда внутри
отрезка [a;b] найдётся такая
точка c, что справедлива формула
отлична
от нуля во всех внутренних точках
отрезка [a;b]. Тогда внутри
отрезка [a;b] найдётся такая
точка c, что справедлива формула
![]()
Последнюю формулу называют формулой Коши или обобщённой формулой конечных приращений.
Доказательство.
Убедимся сначала в том, что знаменатель
левой части формулы Коши не равен нулю
(так как в противном случае это выражение
не имело бы смысла). В самом деле, если
бы было ![]() , то
для функции
, то
для функции ![]() были
бы выполнены все условия теоремы Ролля,
и, следовательно, внутри отрезка [a;b] нашлась
бы такая точка c, что
были
бы выполнены все условия теоремы Ролля,
и, следовательно, внутри отрезка [a;b] нашлась
бы такая точка c, что![]() ,
а это равенство противоречит условию
теоремы. Рассмотрим теперь вспомогательную
функцию
,
а это равенство противоречит условию
теоремы. Рассмотрим теперь вспомогательную
функцию![]() .
.
Функция ![]() удовлетворяет всем условиям теоремы
Ролля. В самом деле, она непрерывна на
отрезке [a;b] (поскольку
непрерывны
удовлетворяет всем условиям теоремы
Ролля. В самом деле, она непрерывна на
отрезке [a;b] (поскольку
непрерывны![]() и
и ![]() ) и
во всех внутренних точках отрезка [a;b] имеет
производную, равную
) и
во всех внутренних точках отрезка [a;b] имеет
производную, равную
![]() .
.
Кроме
того, очевидно, что ![]() . Таким
образом, как следует из теоремы Ролля,
внутри отрезка [a;b] найдётся такая
точка c, что
. Таким
образом, как следует из теоремы Ролля,
внутри отрезка [a;b] найдётся такая
точка c, что![]() , то
есть
, то
есть
![]() , или
, или
![]() .
.
Разделив
это равенство на ![]() (в
данном случае это возможно, та как
(в
данном случае это возможно, та как ![]() ),
получим требуемое равенство.
),
получим требуемое равенство.
Теорема доказана.
49
