
- •Физические основы механики
- •Молекулярная физика и термодинамика
- •Ускорение
- •Поступательное движение
- •Вращательное движение
- •Равномерное движение
- •Равнопеременное движение
- •Виды взаимодействия и силы
- •Центр масс
- •Уравнение движения тела переменной массы
- •Энергия, работа, мощность
- •Решая полученную систему уравнений (1) и (2), находим
- •Решение
|
d(r |
|
) |
|
|
dx |
|
|
|
|
|
d (ry ) |
|
dy |
|
|
|
d(r |
) |
|
dz |
|
||
vx = |
|
|
x |
|
= |
|
|
; vy = |
|
= |
|
; vz = |
z |
|
= |
|
. |
|||||||
|
|
|
|
|
dt |
dt |
dt |
dt |
|
dt |
||||||||||||||
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Модуль скорости находят по формуле |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
v = v2x + v2y + v2z . |
|
|
|
|
|
|||||||
В пределе |
|
|
∆rr |
|
= ∆S, поэтому |
∆S |
|
|
dS |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
v = |
|
vr |
|
= lim |
= |
, |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∆t →0 |
∆t |
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
т. е. численное значение мгновенной скорости равно первой произвольной пути по времени.
В случае неравномерного движения, когда численное значение мгновенной скорости изменяется, можно пользоваться скалярной величиной – средней скоростью ( v ):
v = ∆∆St .
Если выражение dS = v dt проинтегрировать по времени, то найдем путь, пройденный точкой за время ∆t =t2 −t1 :
S = t∫2 v(t) dt.
t1
Ускорение
Физической величиной, характеризующей быстроту изменения скорости по модулю и направлению, является ускорение.
Средним ускорением неравномерного движения называется отношение изменения скорости ∆v к промежутку времени ∆t, за который произошло это изменение:
ar = |
∆v |
= v2 − v1 . |
||
|
∆t |
t |
2 |
−t |
|
|
|
1 |
|
Мгновенным ускорением материальной точки в момент времени t будет предел среднего ускорения:
10
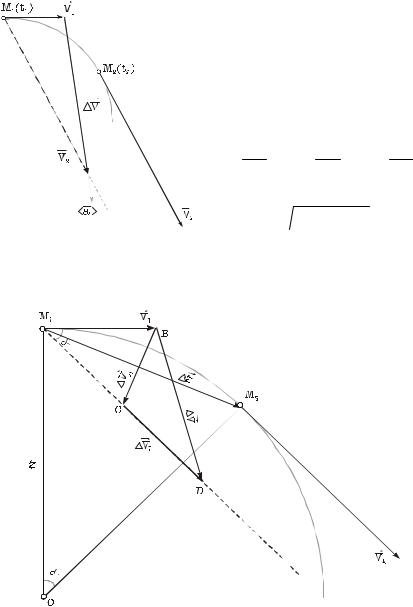
ar = lim |
∆vr |
= |
dvr |
, |
|
∆t |
dt |
||||
∆t →0 |
|
|
т. е. ускорение a есть векторная величина, равная первой производной скорости по времени.
Найдем проекции скорости на оси координат:
ax = ddtvx ; ay = ddtv y ; az = ddtvz ,
тогда
a =
Во многих задачах удобнее раскладывать а на два взаимно перпендикулярных вектора an мальным и тангенциальным ускорениями.
 ax2 + a2y + az2 .
ax2 + a2y + az2 .
aне по осям координат,
иaτ, называемых нор-
Очевидно, что вектор CD, равный ∆vrτ, представляет собой изменение скорости по модулю за время ∆t :
11

∆vτ = v2 −v1.
Вектор ВС, равный |
∆vn , характеризует изменение скорости по |
|||||||||||
направлению. |
|
|
|
|
|
|
|
|
|
|
|
|
Ускорение |
|
|
|
|
|
|
|
|
|
|
|
|
ar = lim |
∆vr |
= lim |
(∆vn + ∆vτ ) |
|
= lim |
∆vn + lim |
∆vτ = arn + arτ. |
|||||
∆t |
|
|||||||||||
∆t→0 |
∆t→0 |
∆t |
|
|
∆t→0 |
∆t |
|
∆t→0 |
∆t |
|||
Тангенциальное ускорение |
|
|
|
|
|
|
||||||
|
|
aτ = lim |
∆vτ |
= lim |
∆v |
= |
dv |
|
|
|||
|
|
∆t |
∆t |
dt |
|
|||||||
|
|
|
|
∆t→0 |
∆t→0 |
|
|
|||||
определяет быстроту изменения величины скорости, оно направлено по касательной к траектории.
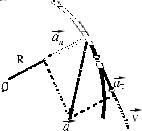
Если промежуток времени ∆t → 0, то точка М2 стремится к М1,
поэтому ∆S можно считать дугой окружности некоторого радиуса r, мало отличающейся от хорды М1М2. Тогда из подобия треугольников М1ВС и М1М2О следует
∆vn = |
M1M 2 |
; ∆vn = |
v1 |
|
|
∆rr |
|
, |
|
|
|
||||||||
OM1 |
r |
||||||||
v1 |
|
|
|
|
|
|
так как M1M 2 = ∆rr . Тогда
|
∆v |
n |
|
v1 |
|
∆rr |
|
|
|
v |
|
|
|
∆rr |
|
|
|
v2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
an = lim |
|
= lim |
|
|
|
|
|
= |
|
1 |
lim |
|
|
|
|
= |
1 |
. |
|
|
r ∆t |
r |
|
∆t |
|
||||||||||||||
∆t→0 |
∆t |
∆t→0 |
|
∆t→0 |
|
|
r |
||||||||||||
Если отбросить индекс при обозначении скорости, то
an = vr2 .
Нормальное (центростремительное) ускорение характеризует быстроту изменения скорости по направлению и направлено перпендикулярно к вектору скорости.
Итак, полное ускорение точки есть геометрическая сумма нормального и тангенциального ускорений:
a = an +aτ или a =  an2 +aτ2 .
an2 +aτ2 .
12
Рассмотрим виды движения материальной точки:
1) an = 0, aτ = 0 – прямолинейное равномерное движение. 2) aτ = a = const, an = 0 – прямоли-
нейноеравнопеременное движение. Проинтегрируем выражение
dv = aτ dt = a dt :
|
v |
r |
t |
r |
dt. |
|
∫dv = ∫a |
||||
Так как ar |
v0 |
|
0 |
|
|
= const , то |
|
|
|
|
|
v = v0 +at,
где vr |
0 – начальная скорость. |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
dS |
|
|
|
Воспользовавшись определением скорости v = |
|
|
|
, можно оп- |
|||||
|
|
dt |
||||||||
ределить пройденный путь: |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||
|
S |
t |
t |
|
t |
t |
|
|
|
|
|
∫dS = ∫v dt = ∫(v0 +at)dt = |
∫v0 dt + |
∫at |
dt, |
|
|||||
тогда |
0 |
0 |
0 |
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S = v0t + |
at 2 |
. |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
3) aτ = f (t), an = 0 |
– прямолинейное движение с переменным ус- |
||||||||
корением. |
|
|
|
|
|
|
|
|
|
|
|
4) aτ = 0, an = const – равномерное движение по окружности. |
|||||||||
|
5) aτ = f (t), |
an ≠ 0 |
– криволинейное движение с переменным ус- |
|||||||
корением.
1 . 2 . КИНЕМАТИКА АБСОЛЮТНО ТВЕРДОГО ТЕЛА
Движение твердого тела можно рассматривать как сумму поступательного и вращательного движений.
Движение твердого тела называют поступательным, если любая прямая, жестко связанная с телом, перемещается, оставаясь параллельной ее первоначальному направлению.
13
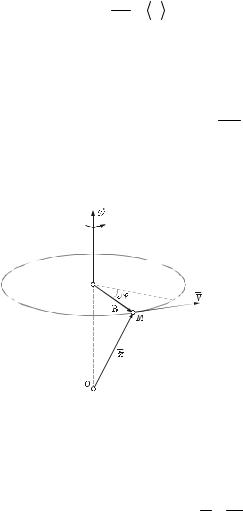
При вращении точки тела описывают окружности, центры которых лежат на оси вращения, а плоскости перпендикулярны к ней.
Для описания вращательного движения вводят понятие угловой скорости и углового ускорения.
Отношение |
∆ϕ |
= ω называют средней угловой скоростью. |
||||
|
∆t |
|
|
|
|
|
Мгновенная угловая скорость |
|
|
|
|
||
|
|
ω= lim |
∆ϕ |
= |
dϕ |
. |
|
|
dt |
|
|||
|
|
∆t →0 |
|
dt |
||
[ω ]= радс .
Вектор угловой скорости направлен по оси вращения, так что его положительное направление составляет с направлением вращения правовинтовую систему, т. е. подчиняется правилу буравчика.
За время dt точка M тела, вращающегося с угловой скоростью ω, проходит по дуге окружности радиуса R путь dS = v dt = R dϕ,
так что
|
|
v = R |
dϕ |
= R ω. |
|
|
|
|
|||
|
|
|
dt |
||
|
|
Если ω = const, то вращение |
|||
|
|
равномерное и его можно характе- |
|||
|
|
ризовать периодом вращения Т – |
|||
|
|
временем, за которое точка совер- |
|||
|
|
шает один полный оборот: |
|||
T = |
2π |
, [T ]= c. |
|||
ω |
|||||
|
|
|
|
||
Частота вращения показывает число оборотов тела в единицу вре-
мени:
н= T1 = 2ωπ,
откуда
ω= 2πн.
14
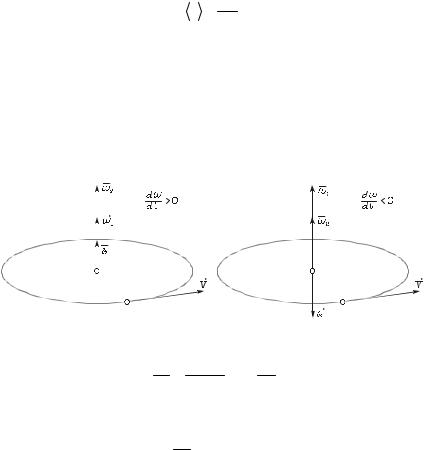
Угловое ускорение
Угловое ускорение вводят при неравномерном вращении. Если за время ∆t угловая скорость изменится на ∆ω, то отношение ∆ω к ∆t называют средним угловым ускорением:
ε = |
∆ω. |
|
|
|
|
|
∆t |
|
|
|
|
Мгновенное угловое ускорение ε = lim |
∆ω |
= |
dω |
. |
|
∆t |
|
||||
|
∆t→0 |
|
dt |
||
[ε]= |
рад. |
|
|
|
|
|
с2 |
|
|
|
|
Из этой формулы следует, что вектор углового ускорения направлен по оси вращения.
Тангенциальное ускорение:
aτ = ddtv = d(dtωR)= R ddtω = R ε.
Нормальное ускорение:
an = v2 = ω2 R2 = ω2 R.
R R
Сопоставим основные уравнения и величины кинематики вращательного движения тела вокруг неподвижной оси и его поступательным движением, подчеркнув их аналогию.
15
