
Плотников А.Н. Статистическое моделирование
.pdfФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
"САМАРСКИЙ ГОСУДАРСТВЕННЫЙ АЭРОКОСМИЧЕСКИЙ УНИВЕРСИТЕТ имени академика С.П. КОРОЛЕВА"
А.Н. ПЛОТНИКОВ
СТАТИСТИЧЕСКОЕ МОДЕЛИРОВАНИЕ И СИСТЕМНЫЙ АНАЛИЗ ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ
Утверждено Редакционно-издательским советом университета в качестве учебного пособия
САМАРА Издательство СГАУ
2008
УДК 519.21 ББК 22.171 П 396
Рецензенты: д-р физ.-мат. наук, проф. А. Ф. К р у т о в д-р техн. наук, проф. В. Д. Ю ш и н
Плотников А. Н.
П396 Статистическое моделирование и системный анализ технологи-
ческих процессов: учеб. пособие / А. Н. Плотников. – Самара: Издво Самар. гос. аэрокосм. ун-та, 2008. – 155 с.
ISBN 978-5-7883-0687-2
Содержит краткое изложение вероятностных основ статистических методов в контексте их практического использования при анализе качества и надежности продукции машиностроительного производства. В главе 1 излагаются общие вероятностные основы и рассмотрены наиболее употребительные выборочные статистики нормальных совокупностей, в том числе порядковые статистики. Основная часть посвящена системам случайных величин и типам их взаимодействий. В главе 2 даны основы дисперсионного анализа и теории планирования эксперимента. В главах 3-5 рассмотрены модели функционирования контрольных, измерительных процессов, основы теории массового обслуживания и схемы статистического регулирования технологических процессов. В качестве иллюстраций приведены примеры статистических экспериментов по методу Монте-Карло, реализованные в пакете Math- cad-2001, которые могут быть использованы для аудиторного и самостоятельного лабораторного практикума по различным приложениям теории вероятностей.
Пособие предназначено для студентов специальностей «Стандартизация и сертификация» и «Управление качеством», а также других специальностей.
УДК 519.21 ББК 22.171
ISBN 978-5-7883-0687-2 |
© Плотников А. Н. |
|
© Самарский государственный |
|
аэрокосмический университет, 2008 |
1 |
2 |
|
ОГЛАВЛЕНИЕ |
|
4.4. Статистическая оценка параметра показательного |
|
|
Введение |
5 |
закона................................................................................... |
122 |
|
Глава 5. Статистическое моделирование случайных процессов |
125 |
|||
|
|
|||
Глава 1. Теоретические основы статистического моделирования |
|
5.1. Модели процессов с непрерывным приращением.......... |
125 |
|
случайных процессов............................................................. |
10 |
5.2. Анализ схем статистического регулирования ................ |
129 |
|
1.1. Преобразования случайных величин и сущность |
|
5.3. Выборочные оценки числовых индексов воспроиз- |
|
|
метода Монте-Карло........................................................... |
10 |
водимости............................................................................ |
138 |
|
1.2. Системы случайных величин.............................................. |
13 |
|
|
|
1.3. Закон совместного распределения выборочных |
|
Список литературы............................................................................... |
144 |
|
значений................................................................................ |
27 |
|
|
|
1.4. Выборочные оценки параметров распределения.............. |
30 |
Приложения........................................................................................... |
145 |
|
|
|
Приложение I. Алгоритмы Монте-Карло, эксперементаль- |
|
|
Глава 2. Основы теории планирования эксперимента....................... |
44 |
ные и расчетные значения инвариантов структуры серий |
|
|
2.1.Факторы эксперимента. Понятие об эффекте фактора….44 |
в последовательной выборке……………………………..…145 |
|||
2.2. Аппарат дисперсионного анализа...................................... |
48 |
Приложение II. Таблица распределения Кохрэна................. |
151 |
|
2.3. Планы со смешиванием эффектов и дробные |
|
Приложение III. Таблица распределения выборочного |
|
|
многофакторные планы....................................................... |
58 |
размаха................................................................................…..153 |
||
2.4.Планы эксперимента для исследования |
|
|
|
|
поверхности отклика……………………………………….69 |
|
|
||
Глава 3. Системный анализ контрольных и измерительных |
|
|
|
|
процессов.................................................................................. |
81 |
|
|
|
3.1. Модель функционирования системы контроля................. |
81 |
|
|
|
3.2. Принцип накопления и анализа информации. Оценка |
|
|
|
|
эффективности контроля..................................................... |
87 |
|
|
|
3.3. Сущность процесса измерения и основные элементы |
|
|
|
|
измерительной системы....................................................... |
92 |
|
|
|
3.4. Модель функционирования измерительной системы....... |
95 |
|
|
|
3.5. Модель функционирования измерительной системы |
|
|
|
|
при приемке по допуску..................................................... |
100 |
|
|
|
Глава 4. Основы теории надежности технологических |
|
|
|
|
и информационных систем................................................... |
102 |
|
|
|
4.1. Потоки случайных событий и их свойства...................... |
102 |
|
|
|
4.2. Парадокс инспекции и смежные вопросы........................ |
109 |
|
|
|
4.3. Очереди и задачи обслуживания....................................... |
112 |
|
|
|
3 |
4 |
|

ВВЕДЕНИЕ
1. Исходным понятием теории вероятностей является случайное событие – событие, которое может произойти или не произойти при воспроизводимой совокупности условий опыта (испытания, наблюдения). Например, появление орла при бросании монеты, выпадение 11 очков при бросании двух игральных костей, попадание в поле допуска размера очередной детали с автоматической производственной линии, существенное улучшение состояния у группы больных после лечения определенным препаратом и т.д. Из перечисленных примеров видно, что каждое событие обладает некоторой степенью возможности. В примере с монетой и игральными костями сразу можно решить, что выпадение орла более возможно, чем выпадение 11 очков при бросании двух игральных костей, а для анализа стабильности технологического процесса или действия лекарственного препарата необходимо иметь фактические результаты наблюдений. С понятием случайного события связано другое фундаментальное понятие теории вероятностей – понятие случайной величины (СВ). Под случайной величиной понимается величина, которая в опыте с несколькими возможными исходами может принимать то или иное значение. Например, число очков при бросании игральной кости, частота появления «орла» в серии повторных опытов с монетой, фактическое количественное значение параметра при контроле и испытаниях промышленной продукции, очередной результат в серии повторных измерений и т.д. Законом распределения случайной величины называется любое правило (функция), позволяющее однозначно определить вероятности возможных значений случайной величины. Наиболее просто обстоит дело, когда множество возможных значений случайной величины конечно либо счетно и может быть отождествлено с пространством событий. Например, появление любого из чисел от «1» до «6» при бросании иг-
ральной кости равновероятно с вероятностью р = 16 ; множество воз-
можных значений частоты появления «орла» при трех бросаниях моне-
|
|
|
|
|
|
|
1 |
|
2 |
|
|
p(0) = p(1) = |
1 |
|
|
ты |
|
составляет v = 0; |
|
; |
|
;1 |
с вероятностями |
8 |
, |
||||||
3 |
3 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
р( |
1 |
) = р( |
2 |
) = |
3 |
. |
|
|
|
|
|
|
|
|
|
3 |
3 |
8 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
Очень важную роль при анализе CB играют ее числовые характеристики, позволяющие определить ее положение на числовой оси, величину рассеивания – степень случайности и форму рассеяния. Важнейшей числовой характеристикой CB является ее среднее значе-
ние или |
математическое ожидание, определяемой как |
∞ |
|
M [X ]= ∑xi pi = μХ . |
|
i=1 |
p(x) понимать дискретное распределение единичной |
Если под |
|
массы на тонком невесомом стержне, то среднее значение можно интерпретировать как x – координату центра масс такой системы. Рассеивание CB около своего среднего значения характеризуется диспер-
сией D[X ]= M [X − μХ ]2 = M [X 2 ]− μХ2 = ∑pk xk2 − μХ2 .
k
В механической интерпретации D[X ] есть момент инерции стержня переменной плотности относительно перпендикулярной оси, проходящей через точку x = M [X ]. Для большей наглядности рассеи-
вание CB характеризуют стандартным или средним квадратичным отклонением (СКО) σx =  D[X ] , которое имеет такую же размерность, что и сама CB. Для более детального описания CB используют
D[X ] , которое имеет такую же размерность, что и сама CB. Для более детального описания CB используют
также асимметрию |
Sx = |
M [X − μХ ]3 |
и эксцесс Ex = |
|
M [X − μХ ]4 |
− 3 . |
(D[X ])3/ 2 |
|
(D[X ])2 |
||||
|
|
|
|
|
||
Для симметричного относительно |
μХ плотности |
распределения |
||||
Sx = 0 , Sx > 0 , если распределение быстрее стремится к нулю слева от μХ , и Sx < 0 – если справа. Эксцесс характеризует рассеивание CB
около среднего значения по сравнению с нормальной CB, у которой Ex=0. Из определения M[X ] и D [ X ] вытекают их следующие свойства:
5 |
6 |
|

– среднее значение неслучайной величины а равно ей самой,
M [a]= a ;
– для любой пары CB Х и Y и неслучайных чисел a и b
M [aX + bY ]= aM [X ]+bM [Y ];
– дисперсия неслучайной величины a равна нулю, D[a]= 0 ;
– для любой пары независимых CB X и Y и неслучайных чисел a и b D[aX +bY ]= a2D[X ]+b2D[Y ].
2. Наиболее употребительными являются следующие виды дис-
кретных CB. Гипергеометрическое распределение в наглядной интер-
претации представляет собой распределение числа черных шаров в случайной выборке или без возвращения из корзины (числа дефектных единиц при выборочном контроле партии штучной продукции). Это распределение совпадает с законом «Спортлото»
|
k n−k |
|
P{Χ = k}= |
CDCN −D |
, где N – объем партии, D – число дефектных еди- |
|
||
|
CNn |
|
ниц, n – объем выборки1. Среднее и дисперсия гипергеометрического распределения равны:
|
|
μ |
Х |
= nD ; σ 2 |
= nD(N − D) |
+ n(n −1) |
D(D −1) |
|
− |
D2 |
. |
|||||||
|
|
|
|
|||||||||||||||
|
|
|
N |
Х |
|
N |
2 |
|
|
|
|
N |
2 |
|
||||
|
|
|
|
|
|
|
|
N(N −1) |
|
|
|
|
|
|||||
|
n |
Биномиальное распределение. |
Рассмотрим асимптотику при |
|||||||||||||||
|
<<1. Разлагая биноминальные коэффициенты через факториалы, |
|||||||||||||||||
|
N |
|||||||||||||||||
|
|
|
k n−k |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
D!(N − D)!n!(N − n)! |
|
|
|
|
|
|
|||||||
получим |
|
CDCN |
−D |
|
= |
|
|
. |
|
|
|
|||||||
|
CNn |
|
k!(D − k)!(n − k)!(N − D − n + k)!N! |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
1 Биномиальный коэффициент Сnm = |
n! |
|
есть число различимых перестановок m |
|
m!(n −m)! |
||||
|
|
|||
красных и n-m белых шаров. При большом количестве цветов полиномиальный коэффициент
определяется как R (n1, n2, n3 ) = (n1 + n2 + n3 )! . n1!n2!n3!
После группировки сомножителей и выделения Cnk , будем иметь
C k |
C n−k |
= C k |
D!(N − D)!(N − n)! |
|
||
D |
N −D |
|
|
. Попарно сокращая факто- |
||
CNn |
(D − k)!(N − D − n + k)!N! |
|||||
n |
|
|||||
риалы числителя и знаменателя, преобразуем последнее выражение к виду
64447k 444864444444n7−k44444448
|
|
Ck D(D −1)...(D − k +1)(N − D)(N − D −1)...(N − D − n + k +1) . |
|||
|
|
n |
|
N(N −1)...(N − n +1) |
|
|
|
|
|
144424443 |
|
|
|
|
|
n=k +n−k |
|
|
Откуда получаем |
асимптотику P{Χ = k}≈ Cnk qk (1−q)n−k , где |
|||
q = |
D |
≈ const . |
|
|
|
N |
|
|
|||
|
|
|
|
|
|
Вчистом виде биноминальное распределение возникает в выборке
свозвращением, когда вероятность успеха каждого испытания не зависит от результатов других испытаний и является величиной постоянной.Числовые характеристики биномиального распределения име-
ют вид: μХ = nq ; σ2Х = nq(1− q).
В предельном случае, когда количество опытов n в испытаниях неограниченно возрастает, а вероятность успеха q неограниченно убывает, но так, что их произведение nq имеет конечный предел:
lim nq = λ .
n→∞ q→0
Перепишем биномиальный закон в виде
|
k |
k |
|
|
n−k |
|
1 |
|
|
λ n |
λ k |
n! |
|
λ |
−k |
||||
Cn q |
|
(1− q) |
|
= |
|
|
1− |
|
|
|
1 |
− |
|
= |
|||||
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
k! |
n n |
(n − k)! |
|
n |
|
|||||
|
1 |
|
|
|
λ n |
k k−1 |
n − т |
λ k |
|
|
|
|
|
||||||
= |
|
|
|
1− |
λ ∏ |
|
|
|
1− |
. |
|
|
|
||||||
|
|
|
|
n |
|
|
|
|
|||||||||||
|
|
k! |
|
n |
т=0 |
|
|
n |
|
|
|
|
|
||||||
Первые три сомножителя на основании второго замечательного |
|||||||||||||||||||
|
|
|
|
|
е−λ |
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
предела дадут |
|
k! |
λ |
. Последний сомножитель при конечном k стре- |
|||||||||||||||
мится к 1. Логарифмируя оставшийся сомножитель, получим
7 |
8 |
|
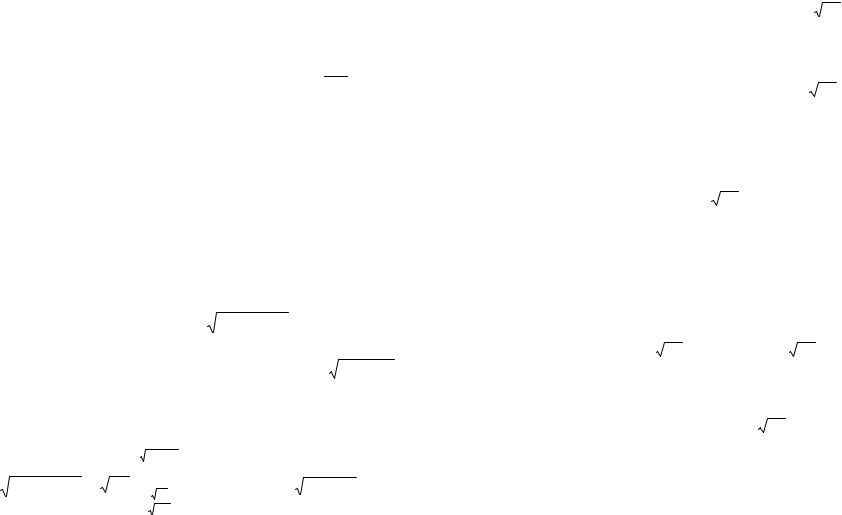
k −1 |
|
|
т |
|
1 |
k −1 |
|
(k −1)k |
|
|
∑ |
ln 1 |
− |
|
|
≈ |
|
∑ |
т = |
|
→0 . |
|
|
|
||||||||
|
|
n |
|
|
|
2n |
n→∞ |
|||
т=1 |
|
|
n т=1 |
|
|
|||||
Таким образом, для распределения числа редких событий получа-
ем асимптотику в виде распределения Пуассона: P{Χ = k}≈ е−λ λk . k!
Помимо рассмотренного «предельного» случая, распределение Пуассона (распределение вероятностей редких событий) является одним из фундаментальных результатов во многих других приложениях теории вероятностей (теория надежности, теория случайных процессов и т.д.). У пуассоновской CB среднее и дисперсия равны между
собой: μХ = σ2Х = λ.
3. Муавр, а позднее независимо от него Лаплас исследовали биномиальное распределение при больших n и установили приближенную формулу (теорема Муавра-Лапласа):
|
|
|
|
|
e− |
(k −nq )2 |
|
|
||
m |
m |
m |
n−m |
m |
2nq(1−q ) |
|
|
|
||
∑Cn q |
|
(1− q) |
≈ ∑ |
|
|
|
. |
|
||
|
2πnq(1− q) |
|
||||||||
k =0 |
|
|
|
k =0 |
|
|
||||
При этом дискретные точки нормированной CB Ζm = |
m − nq |
|||||||||
nq(1− q) |
||||||||||
|
|
|
|
|
|
|
|
|
||
располагаются на числовой оси настолько тесно, что ряд в функции распределения можно заменить интегралом:
|
|
|
1 |
zk2 |
|
|
− |
|
m−nq |
|
|
|
|
|
|
|
m |
e |
− |
|
1 |
|
nq(1−q) |
|
1 |
|
2 |
|
|
||||
|
|
|
|
|
|
|
||||||||||
∑ |
2 |
|
≈ |
|
|
∫ |
e− |
|
z |
dz, где dz ≈ |
1 |
, |
||||
|
|
|
2 |
|||||||||||||
2πnq(1− q) |
2π |
|
nq(1 − q) |
|||||||||||||
k =0 |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
− |
nq |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1−q |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
а нижний предел в интеграле при больших n можно положить равным – ∞.
9
Функция, стоящая под интегралом ϕ0 (z) = |
1 |
e− |
1 |
z |
2 |
|
2 |
, называется |
|||||
2π |
||||||
|
|
|
|
|
плотностью распределения стандартной нормальной случайной величины.
|
1 |
z |
1 |
t |
2 |
|
Функцию распределения CB Z F(z) = |
∫e− |
|
dt удобнее |
|||
2 |
||||||
2π |
||||||
|
−∞ |
|
|
|
||
|
|
|
|
|
представить в виде F(z) = 12 +Ф0 (z) , где Ф0 (z) – функция Лапласа,
или интеграл вероятностей, определяется уравнением
|
1 |
z |
e− |
1 |
t |
2 |
|
Ф (z) = |
∫ |
2 |
dt. |
||||
2π |
|||||||
0 |
|
|
|
|
|||
|
|
|
|
|
|
||
|
|
0 |
|
|
|
|
Таким образом, можно осуществить переход от дискретных CB к непрерывным, важнейшей из которых является именно нормальная
CB.
Плотность распределения и числовые характеристики CB X, связанной с CB Z отношением X=σZ+μ , имеют следующий вид:
|
|
− |
(x−μ)2 |
|
|
|
∞ |
|
− |
(x−μ)2 |
|
|
||
|
e |
2σ 2 |
|
|
|
|
|
2σ 2 |
|
|
||||
|
|
|
|
|
|
e |
|
|
|
|||||
fx (x) = |
|
|
; M [X ]= |
|
∫ |
|
|
|
|
|
xdx = μ ; |
|||
σ 2π |
|
|
σ |
|
2π |
|
||||||||
|
|
|
|
|
|
−∞ |
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
− |
(x−μ)2 |
|
|
|
|
||||
|
|
|
|
|
2σ 2 |
|
|
|
|
|
||||
|
|
|
|
e |
|
|
|
|
|
|
||||
D[X ]= ∫ |
(x − μ)2 |
|
|
|
|
|
|
dx =σ 2. |
||||||
σ |
|
2π |
|
|
||||||||||
|
|
|
−∞ |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Глава 1. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ СТАТИСТИЧЕСКОГО МОДЕЛИРОВАНИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ
1.1.Преобразования случайных величин
исущность метода Монте-Карло
1.Задача установления закона распределения и числовых характеристик функций от случайных величин представляет собой один из основных элементов статистического моделирования. Для простоты
10
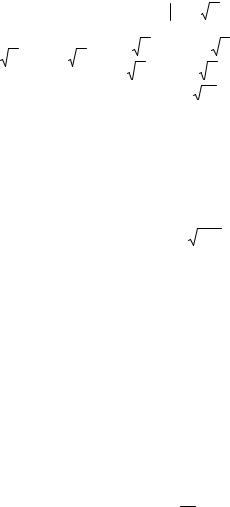
рассмотрим только случай функций c ограниченным количеством интервалов монотонности.
Пусть СВ X и Y связаны между собой соотношением Y=X 2 . В этом случае получим
f y(y) = |
d |
Fy(y) = |
d |
P{Y < y}= |
d |
P{X |
|
|
< |
y}= |
|
|||||||
|
|
|||||||||||||||||
|
|
|
|
|||||||||||||||
|
|
|
|
dy |
|
dy |
|
|
dy |
|
|
|
|
|
(1.1.1) |
|||
|
d |
|
[Fx ( |
y )− Fx (− |
y )]= |
f X ( y ) |
|
f X ( − у) |
|
|||||||||
= |
|
+ |
. |
|
||||||||||||||
|
|
|
|
|
||||||||||||||
|
dy |
|
|
|
2 y |
2 |
y |
|
||||||||||
|
|
Для обратного преобразования Y= |
|
Х будем иметь |
|
|||||||||||||
|
|
|
|
|
|
|
|
fY ( y) = 2yfX ( y2 ) . |
(1.1.2) |
|||||||||
|
|
Эти соотношения используются при построении многих важных |
||||||||||||||||
для практического применения композиционных законов распределения. В частности, если СВ X имеет стандартное нормальное распределение, то СВ Y=X 2 , имеющая плотность распределения
|
e |
− |
1 |
y |
|
|
f y ( y) = |
2 |
|
||||
|
|
, |
(1.1.3) |
|||
|
|
|
||||
|
|
2πy |
|
|||
представляет собой χ12 (Хи-квадрат) с одной степенью свободы и ши-
роко применяется в математической статистике. Среднее и дисперсия СВ с плотностью (1.1.3) равны: M[Y]=1; D[Y]=2.
Пусть случайные величины Y и X связаны соотношением Y = ln X . Найдем ПР fY ( y) :
fY ( y) = |
d |
P{Y < y}= |
|
d |
|
P{X < ey }= ey fX (ey ) . |
(1.1.4) |
||||
dy |
|
dy |
|||||||||
|
|
|
|
|
|
|
|
||||
Для показательного преобразования Y = exp(X ) , обращая (1.1.4), |
|||||||||||
получим |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
f |
Y |
( y) = |
f |
X |
(ln y) . |
(1.1.5) |
|||
|
|
|
|||||||||
|
|
|
|
y |
|
|
|||||
Рассмотрим преобразование Y = X1 . Для ПР fY ( y) получаем
f |
(y) = |
d |
P{Y < y}= |
d |
P X > |
1 |
|
= |
d |
1−F |
( |
1 |
) |
= |
1 |
f |
|
( |
1 |
) . (1.1.6) |
|||
|
|
|
|
|
|
|
2 |
X |
|
||||||||||||||
Y |
|
dy |
dy |
|
y |
|
|
|
X |
|
|
|
|
y |
|
|
y |
||||||
|
|
|
|
|
dy |
|
|
y |
|
|
|
|
|
||||||||||
2. Применим к непрерывной СВ Х собственную ФР, т.е. рассмотрим преобразование Y = FX (X ) . В силу первого свойства ФР величина Y будет сосредоточена на отрезке [0,1]. Для ПР fY(y) полу-чим
f |
y |
(y) = |
d |
|
P{Y < y}= |
d |
|
P{X < F−1(y)}, |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
||||||||||||||||
|
|
dy |
|
|
|
|
|
dy |
|
|
X |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
где F −1 |
– функция, обратная к ФР X , существование которой следу- |
|||||||||||||||||||||
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ет из монотонности FX . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
Продолжив преобразование, получим |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
F |
−1( y) |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
f |
|
( y) = |
d |
|
X |
f |
|
(x)dx = |
|
|
1 |
|
f |
|
[F −1 |
( y)]=1 . (1.1.7) |
|||
|
|
|
|
dy |
∫ |
|
f |
|
[F −1 |
|
|
|||||||||||
|
|
|
|
|
Y |
|
|
X |
|
X |
(y)] |
X |
X |
|
||||||||
|
|
|
|
|
|
|
|
|
−∞ |
|
|
|
|
X |
|
|
|
|
|
|||
Таким образом, автопреобразование Y = FX (X ) переводит любую непрерывную СВ в R(0,1) . Отсюда с очевидностью вытекает и обрат-
ное утверждение: преобразование FX−1 переводит СВ R(0,1) в СВ с ФР FX . Полученное тождество используется при статистическом моделировании случайных процессов методом «Монте-Карло».
Генератор псевдослучайных чисел в серии повторных обращений |
||||||
выдает последовательную выборку из R(0,1) (имитирует рулетку с |
||||||
единичной окружностью). Преобразованием F −1 получается выборка |
||||||
|
|
|
|
|
X |
|
из совокупности |
с |
ФР |
FX . Например, |
преобразование |
||
X = − |
1 |
ln(1 −Y ) |
дает |
СВ |
с показательным |
распределением |
|
||||||
|
λ |
|
|
|
|
|
fX (x) = λe−λx , x ≥ 0 . Все типовые ПР реализованы в качестве стан-
дартных функций в [6].
3. Моделирование целочисленных случайных величин осуществляется путем разбиения единичного отрезка на интервалы, равные вероятностям их возможных значений. Пусть, например, требуется смоделировать (разыграть) полиномиальную СВ, у которой три возможных значения реализуются с вероятностями:
11 |
12 |
|

p1, p2 , p3 =1− p1 − p2 .
Разбивая единичный отрезок на три интервала:
[0, p1]; ( p1, p1 + p2 ]; ( p1 + p2 ,1] ,
интерпретируем попадание равномерной на [0,1] СВ Y в каждый из интервалов как реализацию соответствующего исхода. Если дискретная СВ имеет N равновероятных значений, то моделирующим соотношением будет [NY]+1 , где [·] означает целую часть числа, заключенного в скобки. В качестве примера рассмотрим виртуальный лототрон, реализующий в пакете Mathcad-2001 последовательность независимых тиражей «Спортлото 6 из 49» (рис. 1.1.1). Более содержательные примеры приведены в приложении I.
ns := |
R ← 100 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
n ← 49 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
m ← 6 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
for |
r 1.. R |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
for |
j 1.. n |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
tj ← j |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
for |
i 1.. m |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
jm ← trunc[rnd(1) (n − i + 1)] + 1 |
|
|||||||||||
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
ns i,r ← tjm |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
for |
j jm.. n − i |
if jm ≤ n − i |
|
|
||||||||
|
|
|
|
|
|
|
|
|
tj ← tj+1 |
|
|
|
|
|
|
|
|||
|
return ns |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
1 |
|
2 |
|
3 |
4 |
5 |
|
6 |
7 |
8 |
9 |
10 |
|||
|
|
1 |
1 |
|
35 |
|
1 |
39 |
43 |
|
19 |
24 |
29 |
25 |
48 |
||||
|
|
2 |
11 |
|
15 |
|
27 |
25 |
38 |
|
34 |
37 |
8 |
35 |
8 |
||||
ns = |
3 |
30 |
|
5 |
|
31 |
44 |
49 |
|
1 |
22 |
21 |
7 |
40 |
|||||
|
|
4 |
19 |
|
8 |
|
9 |
47 |
29 |
|
14 |
38 |
26 |
8 |
10 |
||||
|
|
5 |
42 |
|
49 |
|
23 |
26 |
12 |
|
30 |
29 |
38 |
36 |
39 |
||||
|
|
6 |
9 |
|
7 |
|
4 |
21 |
40 |
|
42 |
36 |
9 |
21 |
7 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 1.1.1. Текст программы-имитатора и таблица 10 тиражей
1.2.Системы случайных величин
1.На практике часто бывает необходимо определять вероятности совместной реализации нескольких СВ. Например, если известно, что двигатель автомобиля безотказно работает 100 тыс. км с вероятностью
р1, а ходовая часть с вероятностью р2, то какова вероятность их совместной безотказной работы?
Если эти два события независимы (обозначим их А и В), то вероятность совместного осуществления определяется формулой
13 |
14 |
|

P(AB) = P(A)P(B) . |
(1.2.1) |
Если события не являются независимыми, то вероятность их совместного появления определяется через условную вероятность:
P(AB) = P(A)P(B / A) = P(B)P(A/ B) . |
(1.2.2) |
Под условной вероятностью P(B / A) понимается вероятность на-
ступления события B при условии, что событие A произошло. Для независимых событий P(B / A) = P(B), P(A / B) = P(A) .
Установление независимости событий, либо определение условных вероятностей, часто делается из соображений по существу исследуемого процесса.
Рассмотрим пример. В механизм входят две одинаковые шестерни. Технические условия нарушаются, если они обе окажутся с плюсовыми отклонениями по толщине зуба. У сборщика имеется 10 шестерен, из которых 3 «+» и 7 «-». Определим вероятность нарушения технических условий при сборке. Пусть событие А ~ {первая шестерня «+»}, собы-
тие В ~ |
{вторая шестерня «-»}. По правилу умножения находим |
|||||||||||
P(AB) = P(A)P(B / A) . |
Непосредственным подсчетом находим |
|||||||||||
P(A) = |
3 |
; P(B / A) = |
2 |
; P(AB) = |
3 |
|
2 |
= |
|
1 |
. |
|
|
|
|
|
15 |
||||||||
10 |
9 |
|
10 |
9 |
|
|
||||||
Если же шестерни последовательно устанавливаются на двух рабочих местах и у двух сборщиков одинаковые партии шестерен, то А и В можно считать независимыми. В этом случае
P(B / A) = P(B) = 103 ; P(AB) = P(A)P(B) = 109 .
Из соотношения (1.2.2) следует формула Байеса:
P(B / A) = |
P(B)P(A/ B) |
. |
(1.2.3) |
|
|||
|
P(A) |
|
|
Пусть событие А по условиям опыта может осуществляться только совместно с каким-нибудь из событий полной группы (одной
из гипотез) H1 , H 2 ,KH n , удовлетворяющих условиям
n
∑P(H k ) =1, P(Hi H j ) = 0 при i ≠ j .
k =1
Безусловные вероятности P(Hk ), k =1, n, и априорные условные вероятности P(A / Hk ), k =1, n, предполагаются известными. Тогда вероятность события А определяется формулой полной вероятности:
n |
|
P(A) = ∑P(Hk )P(A/ Hk ) . |
(1.2.4) |
k =1
Апостериорные условные вероятности гипотез Р(Нk/A), то есть правдоподобие гипотез при условии, что событие А зафиксировано, определяются по формуле вероятностей правдоподобия гипотез Байеса:
P(H k / A) = |
P(H k )P(A / H k ) |
. |
(1.2.5) |
n |
|||
|
∑P(H k )P(A / H k ) |
|
|
k =1
Пусть в партии смешаны изделия от трех поставщиков в количестве n1,n2,n3. Известно, что вероятности дефектности для изделия 1-го, 2-го, 3-го поставщиков равны соответственно q1,q2,q3. Взятое наугад изделие оказалось дефектным. Требуется найти вероятность того, что оно принадлежит 1-му, 2-му и 3-му поставщикам.
Пусть событие А ~{изделие оказалось дефектным}. Гипотезы, образующие полную группу, заключаются в следующем:
H1 ~{изделие 1-го поставщика}; H2 ~{изделие 2-го поставщика}; H3 ~{изделие 3-го поставщика}. Их вероятности равны:
P(Hk ) = |
|
nk |
|
, k =1,2,3. |
n1 |
+ n2 |
|
||
|
+ n3 |
|||
Из контекста задачи условные вероятности события А составляют:
P(A/ Hk ) = qk ,k =1,2,3.
Апостериорные вероятности гипотез, вычисленные по формуле Байеса, после элементарных преобразований будут иметь вид
P(Hk / A) = |
|
nk qk |
|
, k =1,2,3 . |
n1q1 |
+ n2q2 |
|
||
|
+ n3q3 |
|||
2. Пусть совокупность объемом N образуется по схеме Бернулли с вероятностью успеха p. Для наглядности представим, что корзина последовательно заполняется N шарами, которые независимо друг от
15 |
16 |
|
друга могут быть черными с вероятностью p и белыми с вероятностью 1 - р . Ряд распределения числа черных шаров будет иметь вид
P{ X = k } = СNk p k (1 − p ) N −k .
Из корзины извлекается безвозвратная выборка объемом n< N. Пусть Y число черных шаров в выборке. Ряд условного выборочного распределения согласно п.1.1 составит
P{Y = m |
|
X = k}= |
CkmCNn−−mk |
, |
|
|
|
||||
|
|
|
CNn |
|
(1.2.6) |
|
|
|
|
m ≤ k ≤ N − n + m .
Найдем ряд безусловного распределения Р{X = m}. Применяя формулу полной вероятности, получим
|
|
N −n+m |
|
|
|
|
|
|
P{Y = m} = ∑P{X = k}P{Y = m | X = k} = |
||||||||
|
|
k =m |
|
|
|
|
|
|
N −n+m |
k |
m |
n−m |
|
k |
|
N −k |
|
= ∑ |
Ck |
CN −k |
p |
(1− p) |
. |
|||
Cn |
|
n |
|
|
||||
k =m |
|
CN |
|
|
|
|
|
|
Комбинаторный множитель в последнем выражении после эле- |
||||||||
ментарных преобразований составит CnmCNk −−mn . Продолжив преобразования, получим
N −n+m
P{Y = m} = Cnm ∑CNk −−mn pk (1− p)N −k =[l = k − m] =
k =m
N −n
= Cnm pm (1− p)n−m ∑CNl −n pl (1− p)N −n−l . l =0
Сумма в последнем выражении представляет собой полную сумму биноминального ряда В (p, N-n), стало быть равна 1.
Таким образом доказана следующая теорема:
Безвозвратная выборка из конечной биноминальной совокупности сохраняет биноминальный закон распределения с той же вероятностью успеха: B( p, N ) → B( p, n) .
3. Рассмотрим другую ситуацию. Пусть имеется двухзвенная технологическая цепь с вероятностями успешного завершения операций p1 и p2 соответственно. Положим, что результаты последовательного
прохождения компонентов полуфабриката (заготовок) независимы в совокупности, т.е. реализуется схема Бернулли. Пусть n – число заготовок, поступивших на вход первого звена. Тогда Y1 – число бездефектных полуфабрикатов на выходе первого звена будет подчиняться биноминальному закону P{Y1=m1}~B(p1,n). Выход первого звена является входом второго, и условное распределение P{Y2=m2 | Y1=m1}, m1 ≥ m2, также будет биноминальным: B(p2 ,m1). Безусловное распределение P{Y2 =m} согласно формуле полной вероятности составит:
|
|
n |
|
|
|
|
_ |
|
|
P{Y2 = m 2 } = ∑ P{Y1 = m 2 }P{Y1 = m 2 | Y 1 |
= m1 } = |
||||||||
|
|
m1 =m 2 |
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
m1 |
m1 |
(1 − p1 ) |
n =m 2 |
m 2 |
m 2 |
(1 − p 2 ) |
m1 −m 2 |
. |
|
= ∑ C n |
p1 |
|
C m1 |
p 2 |
|
|
|||
m1 =m 2 |
|
|
|
|
|
|
|
|
|
Объединяя комбинаторные множители и перегруппировывая факториальные сомножители, получаем тождество
Cnm1 Cmm12 = Cnm2 Cnn−−mm22 = Cnm2 Cnm−1m−m2 2 .
Далее, вынося из под знака суммы множители, не зависящие от m1, искомые вероятности получим в виде
P{Y |
2 |
= m |
2 |
} |
= C m2 ( p p |
2 |
)m2 |
(1 |
− p )n−m2 |
× |
||||||
|
|
|
n |
|
|
1 |
|
|
|
1 |
|
|||||
|
n |
m |
|
−m |
|
1 |
− p |
2 |
|
m1 −m2 |
|
|
||||
|
|
1 |
|
|
2 |
|
|
|
|
|
|
. |
(1.2.7) |
|||
× ∑Cn−m2 |
p1 |
1 |
− p |
|
|
|
|
|||||||||
m1 =m2 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|||
Совершив замену индекса k = m1 − m2 , сумму в последнем выражении преобразуем к виду
n −m2 |
k |
|
|
|
|
1 − p |
2 |
k |
n −m2 |
|
|
|
1 − p |
2 |
k |
n −m2 −k |
|
||||
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|||
∑Cn |
−m2 p1 |
1 |
− p |
|
|
= |
∑Cn −m2 |
p1 |
1 − p |
|
|
1 |
= |
||||||||
k =0 |
|
|
|
|
|
1 |
|
k =0 |
|
|
|
1 |
|
|
|||||||
|
|
|
1 |
− p |
2 |
n −m2 |
|
1 − p p |
2 |
|
n −m2 |
|
|
|
(1.2.8) |
||||||
= 1 |
+ |
p |
|
|
|
|
|
|
|
|
= |
1 |
|
|
. |
|
|
|
|||
|
|
1 |
1 |
− p |
1 |
|
|
|
|
1 − p |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
Возвращая (1.2.8) в (1.2.7), окончательно получаем следующее тождество:
17 |
18 |
|
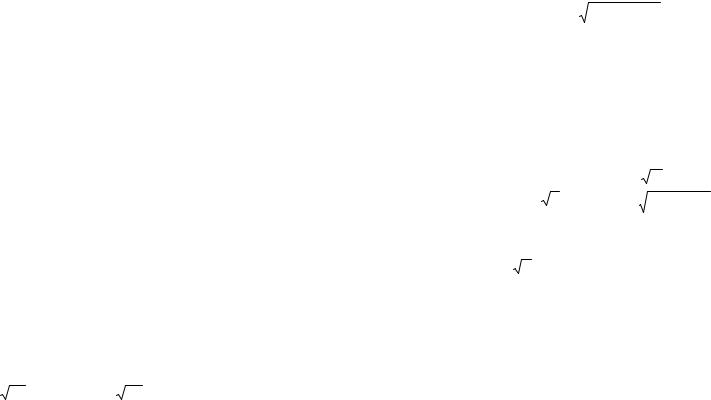
P{Y2 = m2} = Cnm2 ( p1 p2 )m2 (1 − p1 p2 )n −m2 ,
что является доказательством следующей теоремы:
Число успехов при испытаниях по двухзвенной схеме Бернулли подчиняется биноминальному закону с вероятностью успеха, равной произведению вероятностей успеха составляющих звеньев:
B{p1,n}×B{p2,n p1}→ B{p1p2,n).
Из этой теоремы вытекает доказываемое с помощью элементарной индукции следствие: для любого числа последовательных звеньев схемы Бернулли число успехов на выходе подчиняется биноминальному закону с вероятностью успеха, равной произведению вероятностей составляющих звеньев.
4. При совместном рассмотрении нескольких СВ следует различать два принципиально различных типа взаимодействия.
Пусть имеется партия подшипниковых шариков, состоящая из продукции двух различных автоматов. Фактический диаметр шариков первого автомата имеет нормальное распределение с параметрами μ1,σ1 , второго - μ2 ,σ2 . Доли шариков первого и второго сорта равны
соответственно р1 =α, р2 =1−α . Плотность распределения диаметра
шариков в репрезентативной выборке из такой партии по формуле полной вероятности будет равна:
|
|
|
|
|
|
|
|
(d−μ |
)2 |
|
|
|
|
|
(d−μ |
2 |
)2 |
|
|
|
|
|
α |
|
|
|
− |
1 |
|
1 |
−α |
− |
|
|
|
|
|||
f (d ) = |
|
|
|
|
|
2σ 2 |
|
2σ |
2 |
|
|
|
|||||||
|
|
|
e |
|
1 |
+ |
|
|
|
e |
|
2 . |
(1.2.9) |
||||||
|
|
σ 2π |
|
σ |
2 |
2π |
|
||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Если при этом |
|
μ1 − μ2 |
|
|
>σ1 +σ2 , то кривая плотности распреде- |
||||||||||||||
|
|
||||||||||||||||||
ления будет иметь двухмодальный (двухгорбый) вид. Такой тип взаимодействия, когда с вероятностью α появляется СВ X1, a с вероятностью p =1−α – СВ Х2, называется суперпозицией законов распреде-
ления. Если же продукцией автоматов являются, скажем, электрические сопротивления, которые затем соединяются в последовательную цепь, то номинальное сопротивление составных резисторов будет иметь ПР
|
|
|
|
|
(r− |
μ |
−μ |
2 |
)2 |
|
|
|
|
|
|
− |
|
1 |
|
|
|
|
|
f (r) = |
1 |
|
|
2(σ2 |
+σ2 ) |
|
|
||||
|
|
|
|
|
|||||||
|
|
e |
|
|
1 |
|
2 |
|
. |
(1.2.10) |
|
2π(σ2 |
+ σ2 ) |
|
|
|
|
|
|
||||
|
1 |
2 |
|
|
|
|
|
|
|
|
|
Такой тип взаимодействия, представляющий собой сложение независимых СВ, называется композицией.
При этом, если резисторы с двух линий смешиваются в общем накопителе в пропорции p1 =α, p2 =1−α , а затем соединяются в цепь,
то номинал составных резисторов будет иметь трехмодальное распределение с плотностью
|
|
|
|
|
|
|
|
|
(r−2μ |
)2 |
|
|
|
(r−μ −μ |
2 |
)2 |
|
||||
|
|
|
|
α2 |
|
− |
|
|
|
1 |
|
|
2 α(1−α) |
− |
1 |
|
|
|
|||
|
|
|
|
|
|
4σ |
2 |
|
|
2(σ2 |
+σ2 ) |
|
|||||||||
f |
(r) = |
|
|
|
|
e |
|
|
1 |
+ |
|
e |
1 |
|
2 |
|
+ |
||||
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
2σ1 |
π |
|
|
|
|
|
|
|
π 12 + σ22 ) (σ |
|
|
|
|
|||||
|
|
|
|
2 − |
(r−2μ2 )2 |
|
|
|
|
|
|
|
|
|
|
||||||
|
(1− |
α) |
|
4σ |
2 |
|
|
|
|
|
|
|
|
|
|
|
(1.2.11) |
||||
+ |
|
e |
|
2 |
. |
|
|
|
|
|
|
|
|
|
|||||||
2σ2 |
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
В данном случае имеет место совместное проявление суперпозиции и композиции двух СВ. Из этого простого примера ясно, что для результативности и эффективности любого статистического анализа необходимо детальное предметное рассмотрение схемы возникновения и взаимодействия СВ, что на практике нередко упускается из виду.
5. В приложениях математической статистики часто встречается задача установления закона распределения функции нескольких СВ. Сумма двух СВ Y=X1+X2 является частным случаем функции двух СВ. Исчерпывающей характеристикой пары СВ является функция их совместного распределения, которая определяется как вероятность совместности выполнения двух неравенств:
F(х1 , х2 ) = P{Х1 < х1 , Х2 < х2 }. |
(1.2.12) |
Функция распределения (1.2.12) обладает свойствами, аналогичными свойствам функции распределения одной СВ. Однако знание функций распределения F1(x1) и F2(x2) недостаточно для описания совместного распределения X1 и Х2, так как между ними возможно наличие стохастической зависимости — связи. При условии независимости
19 |
20 |
|
