
- •Произведением
- •16. Неупорядоченные выборки с повторениями и без повторений. Разбиение на подмножества.
- •19.Определение условной вероятности. Теоремы умножения зависимых и независимых событий.
- •38 Дискретный случайный вектор
- •Условие независимости для дискретной случайной вел-ны:
- •Условие независимости для непрерывной случайной велечины:
- •Сходимость последовательностей случайных величин
- •49. Закон больших чисел
- •55) Довер-ый интер-л для дисп-ии при неизв-ом мат-ом ожид-ии норм-о распред-ой ген-ой совоку-ти.()
- •Квантили распред-я
- •17.Геометрическое: Классическое определение вероятностей нельзя применять в случае бесконечного числа исходов. К описанию такой ситуации приспособлено геометрическое определение вер-ти.
- •Интеграл Эйлера:
- •Свойства:
- •46 Рассмотрим двумерный случайный вектор (X,y), законы распределения координат которого известны
46 Рассмотрим двумерный случайный вектор (X,y), законы распределения координат которого известны
Пусть z=g(X,Y) - некоторая функция двух переменных, тогдаZ=g(X,Y) – случайная величина. В общем случае закон распределения случайной величины Z найти сложно.
Ограничимся ситуацией, когда g(x,y)=x+y и случайный вектор является непрерывным.
Пусть
 - совместная плотность вероятностей
случайных векторов (X,Y),
Z=X+Y.
- совместная плотность вероятностей
случайных векторов (X,Y),
Z=X+Y.
Требуется найти плотность вероятностей величины Z, сначала найдем функцию распределения:
D={x,y|x+y<z}

Тогда

Аналогично
Если
случайный величины X,Y
независимы, то
 - свертка маргинальных плотностей
вероятностей случайных величин X
и Y.
- свертка маргинальных плотностей
вероятностей случайных величин X
и Y.
В теории вероятностей свертку называют композицией законов распределения.
47В одномерном случае нормальное распределение задается плотностью вероятностей

Пусть (X,Y) – случайный вектор с невырожденной корреляционной матрицей

Тогда обратная матрица к матрице R имеет вид:

Опр. Говорят, что случайный вектор (X,Y) имеет двумерное нормальное (Гауссовское) распределение, если его совместное плотность вероятностей имеет вид:

Свойства нормального вектора (X,Y):
-
Максимальное значение плотности вероятности f(x,y) достигается в точке

-
Маргинальные плотности нормального случайного вектора являются нормальными
-
Условие плотности вероятностей нормального случайного вектора являются нормальными
-
Если случайные величины X и Y нормального случайного вектора (X,Y) не коррелированны (r=0), то они независимы
-
Линейная комбинация нормально распределенных случайных величин является нормально распределенной случайной величиной.

44.Т.1(матожид
ф-ии сл вектора):пусть (Х,У) сл вектор,
Z= -неслуч
ф-я: 1)если (Х,У)-дискрет сл вектор,то
-неслуч
ф-я: 1)если (Х,У)-дискрет сл вектор,то
 (в
предполож что ряд сх-ся абс-но);2)если
(Х,У)-непрер сл вектор,то:
(в
предполож что ряд сх-ся абс-но);2)если
(Х,У)-непрер сл вектор,то: предполож,что
интег-л сх-ся абс-но.
предполож,что
интег-л сх-ся абс-но.
Т.2:мат ожид суммы 2 любых сл величин=сумме их мат ожид-й:

Док-во:для
непрер сл-я:
Т.3:Матожид
произвед-я
2-х независ сл вел-н=произвед их матожид
Док-во:для непрер случая:
M[XY]=M[X]M[Y]=

Опред:Случ
вел-ны для кот кореляц-й момент=0,наз-ся
некоррелированным.Следствие из
Т.3:независ сл вел-ны всегда яв-ся
некоррелированными:
Обратное
неверно,т.е из некоррелированности не
след-ет независ-ть.Некорелир-ть означает
отсутствие линейной связи м/у Х и
У.Другой вид завис-ти может.Можно лишь
утверждать,что из коррелирован-ти = завис-ть случ вел-н,т.е
завис-ть случ вел-н,т.е
 завис-мы
завис-мы
Понятие некоррелированности означает слабую зависимость между х и у и играет важную роль в теории вероятностей.
Т.4(сложение
дисперсий)Если Х,У-любые случ вел-ны,
α, ßєR,
то
 Если
Х,У- некоррелированные, то
Если
Х,У- некоррелированные, то

Док-тво: чтд
чтд
Т.5(Свойства коэффициента корреляции)

Док-тво: ; Положим, что
; Положим, что
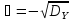 ,
,
 ,
тогда
,
тогда
 ;
;
Полагая
 ,
,
 , то
, то
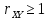 ,
то есть
,
то есть
 чтд
чтд
Т.6:
 верно тогда и только тогда, когда случ
вел-ны X,Y
связаны линейной завис-тью, то есть
верно тогда и только тогда, когда случ
вел-ны X,Y
связаны линейной завис-тью, то есть
 числа А и В, для кот вып-ся
числа А и В, для кот вып-ся

Док-во:
пусть
 ⇒
⇒


Полагая,
что
 ,
,
 ,
получим
,
получим
 при указанных α и ß
при указанных α и ß
Отсюда
получим

Случай
 рассматривается аналогично
чтд
рассматривается аналогично
чтд
Следствие.
Так как
 для независимых случайных величин и
для независимых случайных величин и
 для линейно (сильно) зависимых случайных
величин, то коэффициент корреляции
можно рассматривать как степень
зависимости случайных величин.
Геометрический смысл: чем больше
для линейно (сильно) зависимых случайных
величин, то коэффициент корреляции
можно рассматривать как степень
зависимости случайных величин.
Геометрический смысл: чем больше
 , тем ближе расположены значения
случайных величин X,
Y
к некоторой прямой.
, тем ближе расположены значения
случайных величин X,
Y
к некоторой прямой.
