Условие независимости для дискретной случайной вел-ны:

Если (Х,У) – дискретный случ вектор, то случ вел-ны Х и У независимы.

Доказательство:

Необходимость: Пусть Х и У независимы, Рассмотрим прямоугольник D,содержащий т. (x_i,y_j) и не содержащий других т. случайного вектора.

D: .

P(X=x_i, Y=y_j) = P((X,Y)𝝐D)= F(a2,b2)-F(a1,b2)-F(a2,b1)+F(a1,b1) = [т.к. Х и У независимы то F(a2,b2)=F(a2)F(b2)] = (F(a2)-F(a1)) (F(b2)-F(b1)) = P (a1<X<a2) P(b1<Y<b2) = P(X=x_i) P(Y=y_j)

Достаточность: пусть P(X=x_i, Y=y_j)= P(X=x_i) P(Y=y_j), докажем что в этом случае Х и У независимы:

F(x,y)= = = F(x)F(y) → Х и У независимы по определению.

Условие независимости для непрерывной случайной велечины:

Если (Х,У)- непрерывный случайный вектор, то случ величины Х и У независимы, совместная плотность вероятностей равна произведению маргин. плотностей:

f(x,y) = f(x)f(y)

Доказательство: необходимость: пусть Х и У – независимы, т.е. F(x,y)=F(x)F(y), найдем f(x,y)=

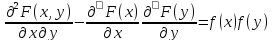
достаточность: Пусть f(x,y)=f(x)f(y) найдем

F(x,y) = → X и У независимы.

Вывод: зная маргин. законы распределения для независимой случайной величины Х и У можно найт совместный закон распределения

43.Матожидание двумерной случ величины (Х,У) наз-ся вектор М[Х,У]=(m_x , m_y)

Условные матожидания: M_x(X I Y=y_j) = I Y=yj) – для дискретной случ величины.

M_x(X I Y=y_j)= I Y=y) dx – для непрерывной случ величины.

Аналогичные формулы имеют место и для случ величины У.

Дисперсией случайного вектора (Х,У) называется вектор: D(Х,У) = (D_x , D_y)

Ковариацией случ величин Х и У называется матожидание от их произведения:

соб [X,Y]=M[XY]=K_xy

Ковариационная матрица: К=

Корреляционный момент: кор момент характеризует связь между велич Х и У. Кор моментом случ велич Х и У называется матожидание от произведения их отклонений

R_xy = M[(X-m_x)(Y-m_y )] (если ковариация центрированных случайных величин)

Вычисление корреляционного момента:

Для дискретных случ величин: R_xy = 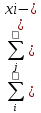m_x)(y_j – m_y)p_ij = p_ij – m_xm_y= M[XY]-M[X]M[Y]

для непрер случ величин:

R_xy = (x-m_x)(y_j – m_y)f(x,y)dxdy = xyf(x,y)dxdy - m_xm_y

Свойства корреляционного момента:

1. Rxx=Dx, Ryy=Dy

2. Ryy=Rxy

Учитывая эти свойства вектор дисперсии можно не рассматривать как отдельную числовую характеристику, а использовать корреляционную матрицу.

R=

Коэффициент корреляции: Корреляционный момент зависит от единиц измерения Х и У. Безразмерным аналогом корреляционного момента является коэф корреляции

r_xy==

Безразмерная корреляционная матрица имеет вид: r==

48. Неравенство Чебышева

Нер-во Чебышева позволяет оценить нер-во для сл.вел. Х , где - заданное положительное число.

Для центриров. а вел-ны нер-во выглядит:

В частности, если , получим:

Таким образом для произвольной а величины правило 36 выполняется в вероятностью не менее, чем 0,(8).