
ФЭУ з/о 0802 менеджмент
Экзаменационные вопросы за первый курс (первая сессия у ускоренников)
-
Определители второго и третьего порядков.
-
Решение систем линейных уравнений по формулам Крамера.
-
Матрицы. Умножение матриц. Обратная матрица.
-
Решение систем линейных уравнений матричным методом.
-
Решение систем линейных уравнений методом Гаусса – Жордана.
-
Уравнение прямой, проходящей через данную точку в данном направлении.
-
Уравнение прямой, проходящей через две данные точки.
-
Векторы. Линейные операции над векторами. Выражение координат вектора через координаты конца и начала.
-
Декартова система координат в пространстве. Координаты вектора. Разложение вектора по базису. Длина вектора.
-
Скалярное произведение векторов.
-
Условия перпендикулярности векторов. Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору.
-
Общее уравнение плоскости.
-
Условия коллинеарности векторов. Канонические и параметрические уравнения прямой.
-
Предел. Теоремы о пределах.
-
Бесконечно малые и бесконечно большие величины. Связь между ними.
-
Замечательные пределы.
-
Непрерывность функции в точке.
-
Свойства функций, непрерывных на отрезке.
-
Производная. Производная постоянной. Производная функции
 .
Дифференциал.
.
Дифференциал. -
Геометрический смысл производной. Уравнение касательной.
-
Производные произведения и частного. Производные функций
 ,
,
 .
. -
Производные функций
 ,
,
 .
. -
Производные функций , .
-
Производная сложной функции. Производные степенной и показательной функций.
-
Теорема Ферма. Необходимое условие экстремума функции.
-
Теорема Ролля. Теорема Лагранжа.
-
Следствия из теоремы Лагранжа. Правило Лопиталя.
-
Знак первой производной и монотонность функции. Достаточное условие экстремума.
-
Знак второй производной и выпуклость функции.
-
Асимптоты функции.
-
Функция двух переменных. Частные производные.
-
Экстремум функции двух переменных. Необходимые и достаточные условия экстремума
Второй курс (вторая сессия для ускоренников)
Программа дисциплины «Математика»
Тема 4. Неопределенный и определенный интегралы
Первообразная. Свойства первообразных. Неопределённый интеграл. Замена перемен-ной в неопределённом интеграле. Линейная замена переменной. Интегрирование по частям в неопределённом интеграле. Определённый интеграл, его свойства и геомет-рический смысл. Формула Ньютона - Лейбница. Замена переменной и интегрирование по частям в определённом интеграле. Несобственные интегралы.
Тема 5. Теория вероятностей
Классическое определение вероятности. Теоремы сложения и умножения вероятностей. Формула полной вероятности. Формула Бернулли. Дискретные случайные величины. Их чис-ловые характеристики. Непрерывные случайные величины. Функция и плотность распреде-ления непрерывной случайной величины. Числовые характеристики непрерывной случайной величины. Нормальный закон распределения.
Рекомендуемая литература
-
Шипачёв В.С. Высшая математика. М., Высшая школа, 1996.
-
Гмурман В.Е. Руководство к решению задач по теории вероятностей и математичес-кой статистике. Москва, «Высшая школа», 2001.
-
Гмурман В.Е. Теория вероятностей и математическая статистика. М., «Высш. шк.», 2001.
Экзаменационные вопросы
-
Первообразная. Свойства первообразных. Неопределённый интеграл.
-
Свойства неопределённого интеграла. Таблица неопределённых интегралов.
-
Замена переменной в неопределённом интеграле. Линейная замена переменной.
-
Интегрирование по частям в неопределённом интеграле.
-
Определённый интеграл, его свойства и геометрический смысл.
-
Интеграл с переменным верхним пределом. Теорема Барроу.
-
Формула Ньютона-Лейбница.
-
Замена переменной в определённом интеграле.
-
Интегрирование по частям в определённом интеграле.
-
Несобственные интегралы первого рода.
-
Классическое определение вероятности.
-
Теорема сложения вероятностей.
-
Теорема умножения вероятностей. Независимость событий.
-
Формула полной вероятности.
-
Формула Бернулли.
-
Функция распределения случайной величины.
-
Математическое ожидание и дисперсия дискретной случайной величины.
-
Непрерывные случайные величины. Функция и плотность распределения.
-
Математическое ожидание и дисперсия непрерывной случайной величины.
-
Нормированное нормальное распределение. Функция Лапласа.
-
Нормальное распределение.
-
Биномиальное распределение.
-
Распределение Пуассона.
Контрольная работа № 2 (в основном потоке выполняется на
втором курсе, а ускоренниками – ко второй сессии первого курса)
Задачи № № 61 – 70, 71 – 80, 81 – 90 из методички для ФЭУ и задачи из общей методички 291 – 300, 301 – 310, 311 – 320, 321 – 330, 331 – 340.
1–10. Задачи на классическое определение вероятности и теоремы сложения, умножения.
1. В одной из коробок 4 белых и 8 чёрных шарика, в другой – 3 белых и 12 чёрных. Из каждой коробки наугад извлекается шарик. Какова вероятность того, что они разноцветные ?
2. Студент выучил 8 из 10 вопросов по первому разделу курса и 9 из 12 – по второму. В билете содержится по одному вопросу из каждого раздела. Какова вероятность получения зачёта для этого студента, если зачёт ставится при условии, что хотя бы на один из вопросов дан правильный ответ ?
3. Проводятся две лотереи. В одной из 100 билетов 20 выигрышных, в другой 120 билетов, среди которых 30 выигрышных. Какова вероятность того, что, имея по одному билету каждой из лотерей, получишь хотя бы один выигрыш ?
4. В одной из коробок 6 белых и 4 чёрных шарика, в другой – 8 белых и два чёрных. Из каж-
дой коробки наугад извлекается шарик. Какова вероятность того, что они оба чёрные ?
5. Студент выучил 5 из 10 вопросов по первому разделу курса и 8 из 12 вопросов – по второму. В билете содержится по одному вопросу из каждого раздела. Какова вероятность получения зачёта для этого студента, если зачёт ставится при условии, что на оба вопроса дан правильный ответ ?
6. Проводятся две лотереи. В одной из 40 билетов 10 выигрышных, в другой 30 билетов, среди которых 15 выигрышных. Какова вероятность того, что, имея по одному билету каждой из лотерей, выиграешь дважды ?
7. В одном из ящиков лежат 6 исправных и 2 неисправные детали, в другом, соответственно 8 и 4. Из каждого ящика наугад берут одну деталь. Какова вероятность того, что только одна из них окажется исправной ?
8. В одной из коробок 5 белых и 10 чёрных шариков, в другой – 3 белых и 9 чёрных. Из каждой коробки наугад извлекается шарик. Какова вероятность того, что хотя бы один из них белый ?
9. Студент выучил 6 из 18 вопросов по первому разделу курса и 4 из 16 – по второму. В билете содержится по одному вопросу из каждого раздела. Какова вероятность того, что студент не сдаст зачёт, если зачёт ставится при условии, что хотя бы на один из вопросов дан правильный ответ ?
10. Проводятся две лотереи. В одной из 20 билетов 5 выигрышных, в другой 25 билетов, среди которых 10 выигрышных. Какова вероятность того, что, имея по одному билету каждой из лотерей, ничего не выиграешь ?
11 – 20. Задачи на формулу Бернулли.
11. Игральную кость бросают 5 раз. Какова вероятность того, что тройка выпадет дважды?
12. Монету бросают 9 раз. Какова вероятность того, что цифра появится в два раза чаще, чем герб ?
13. Какова вероятность того, что в семье, имеющей четверо детей, девочек и мальчиков поровну ?
14. Вероятность попадания в цель при одном выстреле 0,8. Какова вероятность двух промахов при шести выстрелах ?
15. Монету бросают 8 раз. Какова вероятность того, что орёл и решка выпадут поровну ?
16. Игральную кость бросают 6 раз. Какова вероятность того, что чётное число очков выпадет трижды ?
17. Вероятность попадания в цель при одном выстреле 0,7. Какова вероятность только одного попадания при трёх выстрелах ?
18. Игральную кость бросают 6 раз. Какова вероятность того, что дважды выпадет число очков, делящееся на три ?
19. Бросают 5 монет. Какова вероятность того, что только на одной из них выпадет герб ?
20. Игральную кость бросают 6 раз. Какова вероятность того, что нечётное число очков выпадет в два раза чаще, чем чётное ?
21 – 30. Дискретная случайная величина задана своим законом распределения. Заполнить пу-стую клетку таблицы и найти математическое ожидание, дисперсию и среднее квадратичес-кое отклонение данной случайной величины. Построить график её функции распределения.
|
21. |
X |
– 4 |
0 |
5 |
22. |
X |
0 |
2 |
6 |
|
|
P |
0,1 |
0,8 |
|
P |
0,7 |
|
0,1 |
|
23. |
X |
–3 |
–1 |
0 |
24. |
X |
–1 |
0 |
5 |
|
|
P |
|
0,2 |
0,6 |
P |
0,4 |
0,5 |
|
|
25. |
X |
0 |
3 |
4 |
26. |
X |
– 4 |
–2 |
0 |
|
|
P |
0,8 |
|
0,1 |
P |
|
0,2 |
0,7 |
|
27. |
X |
–2 |
0 |
4 |
28. |
X |
0 |
1 |
3 |
|
|
P |
0,3 |
0,6 |
|
P |
0,5 |
|
0,2 |
|
29. |
X |
–2 |
–1 |
0 |
30. |
X |
–2 |
0 |
1 |
|
|
P |
|
0,3 |
0,4 |
P |
0,2 |
0,3 |
|
31– 40. Непрерывная случайная величина задана функцией распределения F(x). Найти математическое ожидание, дисперсию и среднее квадратическое отклонение этой случайной величины. Построить графики функции и плотности распределения.
31.
 32.
32.
 33.
33.
 34.
34. 35.
35. 36.
36.
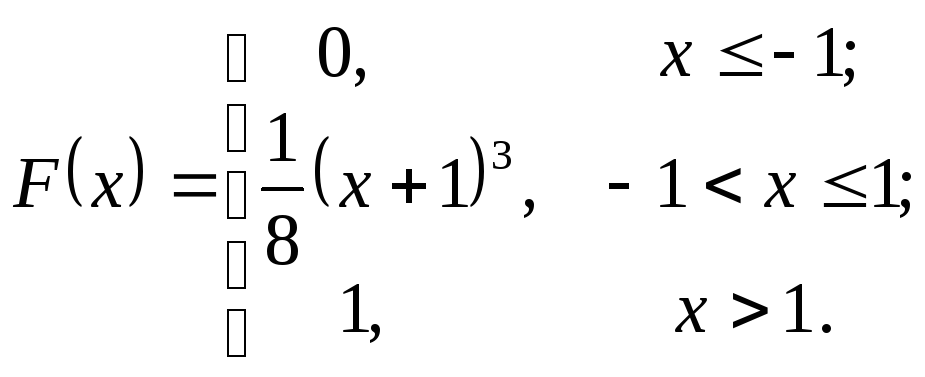
37.
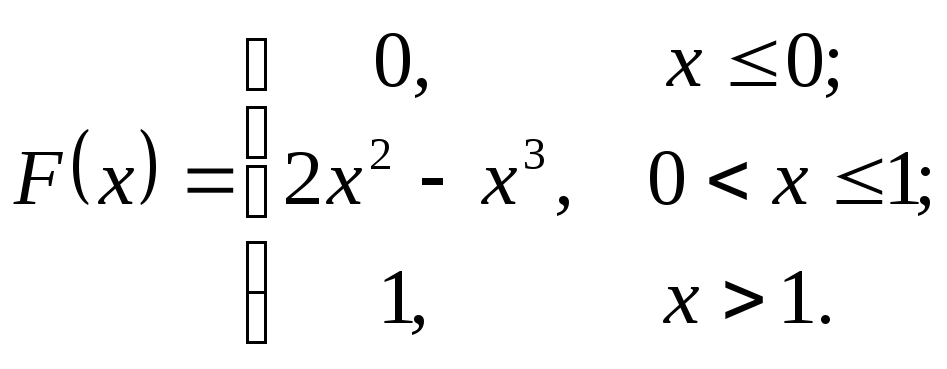 38.
38.

39.
 40.
40.

41– 50. Случайная величина X имеет нормальное распределение с математическим ожи-данием a и средним квадратическим отклонением s. Найти вероятность попадания этой случайной величины в интервал (a, b ).
41. a =42, s =12, a =36, b =54. 42. a =12, s =4, a =6, b =16. 43. a =25, s =5, a =15, b =30. 44. a =15, s = 6, a = 6, b =18. 45. a = 40, s =10, a = 35, b =55. 46. a = 7, s = 2, a = 2, b = 10. 47. a = 17, s = 3, a = 14, b = 23. 48. a = 9, s = 2, a =11, b = 14. 49. a = 10, s = 4, a = 8, b = 18. 50. a = 37, s = 7, a = 30, b = 44.
Комментарии
1–10.
Если
элементарные исходы испытания
равновозможны, а число их конечно,
вероят-ность события A
вычисляется
по формуле
![]() ,
где n
–
число всех элементарных исхо-дов
испытания,
m
–
число элементарных исходов испытания,
благоприятствующих появле-нию события
A
(классическое определение вероятности).
,
где n
–
число всех элементарных исхо-дов
испытания,
m
–
число элементарных исходов испытания,
благоприятствующих появле-нию события
A
(классическое определение вероятности).
Например, вероятность выпадения двойки при бросании игральной ости (кубика, на гра-нях которого нанесены числа очков от 1 до 6) равна 1/6, а вероятность наугад вытащить из урны красный шарик при условии, что в ней находится 3 красных и 4 синих, равна 3/7.
Вероятность того, что происходит хотя бы одно из событий A и B, то есть вероятность по-явления события A + B, можно вычислить по формуле P ( A + B ) = P ( A ) + P ( B ) – P ( A B ).
Вероятность того, что происходят оба события (и событие A, и событие B), то есть вероят-ность произведения этих событий P ( A B), можно вычислить, при условии, что A и B независимы, по формуле P ( A B ) = P ( A ) P ( B ).
Вероятность
события
![]() ,
противоположного событию A,
то есть события, состоящего в том,
что A
не
происходит, находится по формуле P
(
,
противоположного событию A,
то есть события, состоящего в том,
что A
не
происходит, находится по формуле P
(![]() )
=1 –
P
(
A
).
)
=1 –
P
(
A
).
В
некоторых задачах этой серии событие,
вероятность которого нужно определить,
можно представить как
![]() .
.
11
– 20.
Пусть проводится серия из n
независимых испытаний, в каждом из
которых ве-роятность появления события
A
равна
p.
Тогда вероятность того, что в этой серии
событие A
наступит ровно k
раз,
![]() ,
вычисляется по формуле Бернулли.
,
вычисляется по формуле Бернулли.
![]() =
=![]() ,
где
,
где
![]() ,
а q
=
1 – p.
Вычисляя p,
если оно неизвестно, следует помнить,
что p
=
P
(
A
);
а P
(
A
)
– это вероятность появления A
при одном (отдельно взятом) испытании,
так что числа n
и
k
при
вычислении p
заведомо не следует использовать.
,
а q
=
1 – p.
Вычисляя p,
если оно неизвестно, следует помнить,
что p
=
P
(
A
);
а P
(
A
)
– это вероятность появления A
при одном (отдельно взятом) испытании,
так что числа n
и
k
при
вычислении p
заведомо не следует использовать.
|
X |
x1 |
x2 |
... |
xi |
... |
xn |
|
P |
p1 |
p2 |
... |
pi |
... |
pn |
31–
40.
Математическое ожидание и дисперсия
непрерывной случайной величины X
вычисляются
по формулам
![]() =
=![]() ,
где плотность распределения
,
где плотность распределения
![]() ;
;
![]() =
=![]() –
–![]() ,
где
,
где
![]() =
=![]() .
Рассмотрим пример. Пусть
.
Рассмотрим пример. Пусть
![]()
 Тогда
Тогда

![]()
![]()
![]() .
.![]() .
Среднее квадратическое отклонение
вычис-ляется по формуле
.
Среднее квадратическое отклонение
вычис-ляется по формуле
![]() .
В нашем случае
.
В нашем случае
![]() .
Построим графики функции и плотности
распределения.
.
Построим графики функции и плотности
распределения.


41
– 50.
Вероятность попадания нормально
распределённой случайной величины в
заданный интервал вычисляется по формуле
![]() ,
где
,
где
![]() – функция Лапласа, задаваемая формулой
– функция Лапласа, задаваемая формулой
 .
Приближённые значения функции Лапла-са
можно найти по таблицам, имеющимся в
любом учебнике по теории вероятностей.
Вот некоторые значения функции Лапласа.
F(0,5)
@
0,1915; F(1)
@
0,3413; F(1,5)
@
0,4332; F(2)
@
0,4772; F(2,5)
@
0,4938. Отметим, что функция Лапласа
нечётная, то есть
.
Приближённые значения функции Лапла-са
можно найти по таблицам, имеющимся в
любом учебнике по теории вероятностей.
Вот некоторые значения функции Лапласа.
F(0,5)
@
0,1915; F(1)
@
0,3413; F(1,5)
@
0,4332; F(2)
@
0,4772; F(2,5)
@
0,4938. Отметим, что функция Лапласа
нечётная, то есть
![]() =
–
=
–![]() .
.
