
metod_k5_2011_v2
.pdfФедеральное государственное образовательное |
. |
|
|
бюджетное учреждение высшего профессионального |
|
образования |
|
«ФИНАНСОВЫЙ УНИВЕРСИТЕТ |
|
ПРИ ПРАВИТЕЛЬСТВЕ РОССИЙСКОЙ ФЕДЕРАЦИИ» |
|
(ФИНУНИВЕРСИТЕТ) |
|
Кафедра |
|
«Теория вероятностей и математическая статистика» |
|
A.В. Браилов П.Е. Рябов
Теория вероятностей и математическая статистика
Методические рекомендации по самостоятельной работе
Часть 5
Для студентов, обучающихся по направлению 080100.62 «Экономика»
(программа подготовки бакалавра)
Москва 2011

Федеральное государственное образовательное бюджетное учреждение высшего профессионального образования
«ФИНАНСОВЫЙ УНИВЕРСИТЕТ ПРИ ПРАВИТЕЛЬСТВЕ РОССИЙСКОЙ ФЕДЕРАЦИИ»
(ФИНУНИВЕРСИТЕТ)
Кафедра «Теория вероятностей и математическая статистика»
УТВЕРЖДАЮ
Ректор М.A. Эскиндаров
« |
|
» |
|
2011 г. |
A.В. Браилов П.Е. Рябов
Теория вероятностей и математическая статистика
Методические рекомендации по самостоятельной работе
Часть 5
Для студентов, обучающихся по направлению 080100.62 «Экономика»
(программа подготовки бакалавра)
Рекомендовано Ученым советом факультета математических методов и анализа рисков (протокол № 13 от 22 февраля 2011 г.)
Одобрено кафедрой «Теория вероятностей и математическая
статистика» (протокол № 6 от 3 февраля 2011 г.)
Москва 2011
УДК |
519.2(072) |
|
|
XXXX |
ББК |
22.17я 73 |
|
|
|
Б 87 |
|
|
|
|
|
Рецензент: |
В.Б. Горяинов – |
к.ф.-м.н., доцент |
|
|
|
кафедры «Математическое моделиро- |
||
|
|
вание», МГТУ им. Н.Э. Баумана |
||
Б 87 |
Браилов А.В., Рябов П.Е. Теория вероятно- |
|||
|
стей и математическая статистика. Методиче- |
|||
|
ские рекомендации по самостоятельной работе. |
|||
|
Часть 5. – М.: Финуниверситет, кафедра «Тео- |
|||
|
рия вероятностей и математическая статисти- |
|||
|
ка», 2011. – 72 с. |
|
|
|
|
Методические рекомендации предназначены для |
|||
|
организации |
самостоятельной |
работы |
студентов, |
|
изучающих дисциплину «Теория вероятностей и ма- |
|||
|
тематическая статистика». В теоретической справке |
|||
|
приведены решения типовых задач, которые вошли |
|||
|
в варианты контрольных работ. Учебное издание |
|||
|
содержит 30 вариантов контрольных заданий, требо- |
|||
|
вания к оформлению домашней контрольной работы. |
|||
|
В конце учебного издания приведена рекомендуемая |
|||
|
литература. |
|
|
|
|
|
|
УДК |
519.2(072) |
|
|
|
ББК |
22.17я 73 |
Учебное издание
Браилов Андрей Владимирович Рябов Павел Евгеньевич
Теория вероятностей и математическая статистика Методические рекомендации
по самостоятельной работе Часть 5
Компьютерный набор, верстка Рябов П.Е. Формат 60× 90/16. Гарнитура Times New Roman Усл. 4,4 п.л. Изд. № 34.11 – 2011. Тираж – 206 экз.
Заказ № Отпечатано в Финуниверситете
c Браилов Андрей Владимирович, 2011c Рябов Павел Евгеньевич, 2011
c Финуниверситет, 2011
Содержание
§1. Эмпирические характеристики признаков .......... 5 §2. Межгрупповая дисперсия...........................10 §3. Интервальные характеристики признака .......... 12 §4. Повторные и бесповторные выборки ............... 13 §5. Выборки из распределения ......................... 26 §6. Точечные статистические оценки .................. 29 §7. Доверительные интервалы.......................... 34 Требования к оформлению домашней контрольной работы .................................... 38
Вариант № 5-01.........................................39 Вариант № 5-02.........................................40 Вариант № 5-03.........................................41 Вариант № 5-04.........................................42 Вариант № 5-05.........................................43 Вариант № 5-06.........................................44 Вариант № 5-07.........................................45 Вариант № 5-08.........................................46 Вариант № 5-09.........................................47 Вариант № 5-10.........................................48 Вариант № 5-11.........................................49 Вариант № 5-12.........................................50 Вариант № 5-13.........................................51 Вариант № 5-14.........................................52 Вариант № 5-15.........................................53 Вариант № 5-16.........................................54 Вариант № 5-17.........................................55 Вариант № 5-18.........................................56 Вариант № 5-19.........................................57 Вариант № 5-20.........................................58 Вариант № 5-21.........................................59 Вариант № 5-22.........................................60 Вариант № 5-23.........................................61 Вариант № 5-24.........................................62
Вариант № 5-25.........................................63 Вариант № 5-26.........................................64 Вариант № 5-27.........................................65 Вариант № 5-28.........................................66 Вариант № 5-29.........................................67 Вариант № 5-30.........................................68 Рекомендуемая литература ............................ 69
3 |
4 |

§1. Эмпирические характеристики признаков
Одним из первых понятий, с которых начинается изложение математической статистики, является понятие признака. В сущности, признак – это то же самое, что функция, только без явной привязки к некоторой области определения. Вместо термина признак иногда используется равнозначный термин переменная. Признаки обозначаются так же, как и случайные величины – большими латинскими буквами: X ,Y и т.д.
Рассмотрим признак X , заданный на некотором множестве (статистической совокупности) Ω = {ω1 ,...,ωn }. Пусть x1 = X (ω1 ), . . . , xn = X (ωn ) – его значения.
Определение. Эмпирическим средним или средним значением признака в совокупности Ω называется сред-
нее арифметическое всех его значений в этой совокуп-
ности
x¯ = x1 + x2 + ... + xn . n
Определение. Эмпирической дисперсией или дисперсией признака X в совокупности Ω называется среднее
арифметическое квадратов отклонений его значений от эмпирического среднего
D (X ) = (x1 − x¯)2 + (x2 − x¯)2 + ... + (xn − x¯)2 , n
√
при этом корень σ = D (X ) называется стандартным отклонением признака X в совокупности Ω .
Эмпирические начальные и центральные моменты k- го порядка признака X определяются соотношениями:
|
xk |
+ xk |
+ ... + xk |
|
ν (X ) = |
1 |
2 |
n |
– начальный момент и |
|
|
|
||
k |
|
|
n |
|
|
|
|
||
µk (X ) = |
(x1 − x¯)k + (x2 − x¯)k + ... + (xn − x¯)k |
|||
|
|
|
|
n |
– центральный момент.
5
В этих формулах k = 1, 2, ... – порядок эмпирического момента.
Наконец, эмпирическая функция распределения F (x)
определяется так:
F (x) = {число элементов ω Ω , для которых X (ω ) < x}. n
Обозначения эмпирических моментов и функции распределения зависят от обозначения статистической совокупности. Если, например, признак X определен на совокупности Ωˆ , эмпирические моменты обозначаются νˆk
и µ , а функция распределения – ˆ .
ˆ k F (x)
Введенные эмпирические понятия обладают всеми свойствами своих теоретико-вероятностных аналогов. Например, хорошо известное в теории вероятностей
тождество
D (X ) = E (X 2) − E 2(X )
применительно к признаку X со значениями x1 , ..., xn на
ˆ |
|
|
|
|
совокупности Ω , дает следующее соотношение для эмпи- |
||||
рической дисперсии: |
|
|
|
|
ˆ |
− νˆ |
2 |
2 |
2 |
D (X ) = νˆ2 |
1 |
= x |
− x¯ . |
|
Упорядочив значения x1 , ..., xn по неубыванию, получим вариационный ряд признака
x(1) 6 x(2) 6 ... 6 x(n−1) 6 x(n) .
Разность между наибольшим и наименьшим значением x(n) − x(1) называется размахом признака.
Порядковый центр (середина) вариационного ряда называется эмпирической медианой и определяется формулой
x(k+1) , если n = 2k + 1,
M e = 1
2 x(k) + x(k+1) , если n = 2k.
6
Эмпирические квантили порядка p определяются как приближенные решения уравнения F (x) = p, где F (x) – эмпирическая функция распределения.
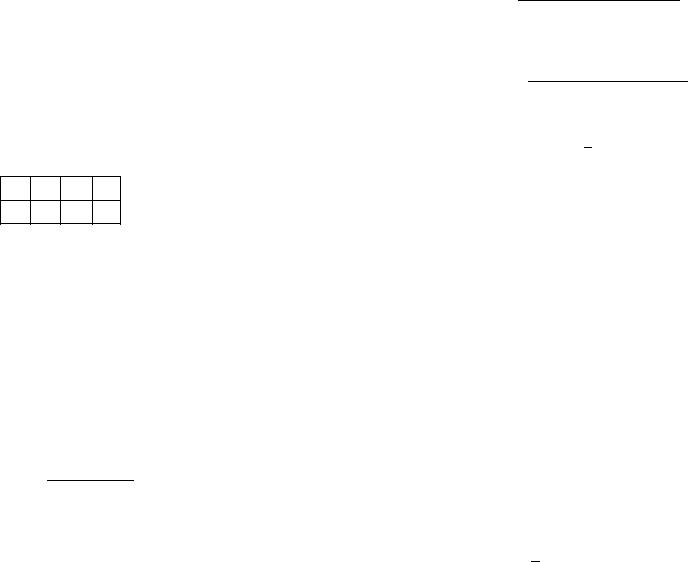
Пусть X – признак в совокупности Ω объема n. Список всех его значений образует ряд из n чисел. Удалив из него одинаковые числа и пронумеровав заново то, что осталось, получим последовательность x1 ,... ,xs, s 6 n.
Определение. Количество ni элементов ω Ω , для которых X (ω ) = xi называется частотой значения xi . Отно-
шение ni называется относительной частотой xi . При |
||
n |
|
|
этом таблица частот значений |
|
|
x1 |
x2 ... |
xs |
n1 |
n2 ... |
ns |
называется частотным (или статистическим) рас-
пределением, а таблица относительных частот
x1 |
x2 |
... |
xs |
|
n1 |
n2 |
... |
ns |
|
n |
n |
n |
||
|
называется эмпирическим распределением признака.
Эмпирические характеристики признака находятся по таблицам частот следующим образом:
• эмпирическое среднее
x¯ = x1n1 + ... + xsns , n
• эмпирический начальный момент порядка k
|
xk n1 |
+ ... + xk ns |
|
vk = |
1 |
s |
, |
|
n |
||
|
|
|
|
|
7 |
|
|
• эмпирический центральный момент порядка k
µk = (x1 − x¯)k n1 + ... + (xs − x¯)k ns , n
• эмпирическая дисперсия
D (X ) = (x1 − x¯)2 n1 + ... + (xs − x¯)2 ns , n
• эмпирическая функция распределения
F (x) = 1 ∑ ni .
n xi <x
Пусть xi = X (ωi ) и yi = Y (ωi ), ωi Ω – значения признаков X и Y на совокупности Ω = {ω1 ,... ,ωn }. Эмпирическая ковариация определяется формулой
|
1 |
n |
COV(X ,Y ) = |
|
∑ (xi − x¯)(yi − y¯). |
n |
||
|
|
i=1 |
Таблицей сопряженности или совместным частотным распределением признаков X и Y называется следующая таблица:
|
Y = y1 |
Y = y2 |
... |
Y = ys |
|
|
|
|
|
X = x1 |
n11 |
n12 |
... |
n1s |
... |
... |
... |
... |
... |
|
|
|
|
|
X = xr |
nr1 |
nr2 |
... |
nrs |
где ni j – частота пары (xi ,y j ), т.е. число элементов ω Ω , для которых X (ω ) = xi , а Y (ω ) = y j .
На основе таблицы сопряженности эмпирическая ковариация находится по формуле:
1 r s
COV(X ,Y ) = ∑ ∑ (xi − x¯)(y j − y¯)ni j .
n i=1 j=1
8

Эмпирический коэффициент корреляции признаков определяется тем же соотношением, что и коэффициент корреляции случайных величин:
COV(X ,Y )
ρ (X ,Y ) = √ .
D (X )D (Y )
Пример 1. В совокупности 16 студентов определены два признака: X – оценка по математике и Y – оценка по
иностранному языку. Совместное частотное распределение оценок задано таблицей:
|
X = 2 |
X = 3 |
X = 4 |
X = 5 |
|
|
|
|
|
Y = 3 |
1 |
0 |
1 |
0 |
|
|
|
|
|
Y = 4 |
2 |
4 |
4 |
2 |
|
|
|
|
|
Y = 5 |
0 |
1 |
0 |
1 |
|
|
|
|
|
Требуется найти эмпирический коэффициент корреляции ρ (X ,Y ).
Решение. Сначала находим частотные распределения при-
знаков:
Значение X |
2 |
3 |
4 |
5 |
|
|
|
|
|
Частота |
3 |
5 |
5 |
3 |
|
|
|
|
|
и |
Значение Y |
3 |
4 |
5 |
|
|
|
|
|
||
Частота |
2 |
12 |
2 |
||
|
|||||
|
|
|
|
|
Затем последовательно вычисляем |
|
|
|
||||||
x¯ = |
1 |
(2 × 3 + 3 × 5 + 4 × 5 + 5 |
× 3) = 3,5; |
||||||
|
|||||||||
16 |
|||||||||
|
1 |
|
(2 − 3,5)2 × 3 + (3 |
− 3,5)2 × 5+ |
|||||
D (X ) = |
|
|
|||||||
16 |
|||||||||
+(4 |
3 5)2 |
5 + (5 |
3 5)2 |
× |
3 = 1; |
||||
|
− , |
× |
− , |
|
|
||||
y¯ = 161 (3 × 2 + 4 × 12 + 5 × 2) = 4;
9
( |
) = |
1 |
|
|
(3 |
|
4)2 |
|
2 + (4 |
|
4)2 |
|
12 + (5 |
|
4)2 |
|
2 |
= |
1 |
; |
||
|
|
|
|
|
|
|
|
|||||||||||||||
D Y |
|
16 |
|
1− |
|
× |
|
− |
|
× |
|
− |
|
×1 |
|
|
4 |
|
||||
COV(X ,Y ) = |
|
|
((1,5) + (−0,5) + (−0,5) + (1,5)) = |
|
; |
|
|
|||||||||||||||
|
16 |
8 |
|
|
||||||||||||||||||
ρ (X Y ) = |
|
1/8 |
|
= 0 25 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Ответ: 0, |
,25. |
|
p1/4 |
|
, . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
§2. Межгрупповая дисперсия
Пусть X – признак в совокупности Ω объема n, разбитой на s групп:
Ω i = {ωi1 , ωi2 , ... , ωini }, i = 1,...,s.
Введем следующие обозначения:
xi j = X (ωi j )
– значение признака на j-м элементе i-ой группы;
|
1 |
ni |
|
|
x¯i = |
∑ xi j |
(1) |
||
n |
||||
|
i j=1 |
|
||
– эмпирическое среднее в i-ой группе или i − групповое среднее;
|
1 |
ni |
|
|
σi2 = |
∑ (xi j − x¯i)2 |
(2) |
||
|
||||
ni |
||||
|
|
j=1 |
|
– эмпирическая дисперсия в i-й группе или i − групповая дисперсия;
1 |
k |
|
1 |
k ni |
|
|
|
x¯ = |
|
∑ |
x¯i ni = |
|
∑ ∑ |
xi j |
(3) |
n |
n |
||||||
|
i=1 |
|
i=1 j=1 |
||||
|
|
|
|
|
|
||
– эмпирическое среднее во всей совокупности Ω или общее среднее;
|
1 |
k |
|
||
σ¯ 2 |
= |
|
∑ σi2ni |
(4) |
|
n |
|||||
|
|
i=1 |
|
||
|
|
|
|
||
10

– средняя групповая дисперсия; |
|
||||
|
|
1 |
k |
|
|
δ 2 = |
|
∑ (x¯i − x¯)2 ni |
(5) |
||
n |
|||||
|
|
|
|
i=1 |
|
– межгрупповая дисперсия. |
|
||||
1 |
|
k ni |
|
||
σ 2 = |
|
|
∑ ∑ (xi j − x¯)2 |
(6) |
|
|
|
||||
ni=1 j=1
–эмпирическая дисперсия признака в Ω или общая дисперсия.
Общую дисперсию σ 2 можно представить в виде сум-
мы
σ 2 = σ¯ 2 + δ 2 , |
(7) |
где первое слагаемое σ¯ 2 характеризует среднюю изменчивость признака в каждой группе Ω 1, ... , Ω k , а второе слагаемое δ 2 характеризует разброс групповых средних x¯1 , ... , x¯k .
Пример 2. Пусть некоторая совокупность разбита на две равные по объему группы. Предположим, что в первой группе среднее значение признака x¯1 = 10, дисперсия σ12 = 15, а во второй группе x¯2 = 20, σ22 = 25. Найдите сред-
нее значение и дисперсию признака во всей совокупности.
Решение. Сначала находим среднее, затем дисперсию:
x¯ = x¯1 |
n1 |
+ x¯2 |
n2 |
= 10 · |
1 |
+ 20 · |
1 |
= 15, |
|
|
|
||||||||
|
n |
|
n |
|
2 |
2 |
|
|
|
||||||||||
σ 2 = σ¯ 2 + δ 2 = |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
n1 |
|
|
n2 |
|
|
|
|
n1 |
|
|
n2 |
|
|||||
= σ12 |
|
+ σ22 |
|
|
+ |
(x¯1 − x¯)2 |
|
+ (x¯2 |
− x¯)2 |
|
= 20 + 25 = 45. |
||||||||
n |
n |
|
n |
n |
|||||||||||||||
Ответ: x¯ = 15, σ 2 = 45.
§3. Интервальные характеристики признака
Пусть (a1 , b1 ), ... , (as , bs) – набор попарно непересекающихся интервалов, покрывающих все значения признака X в совокупности Ω объема n.
Определение. Частотой интервала (ai , bi ) называется число тех элементов ω Ω , для которых X (ω ) (ai ,bi ); интервал (ai ,bi ) при этом называется i-м интервалом
группировки.
Таблицей интервальных частот называется табли-
ца
a1 |
b1 |
n1 |
|
|
|
a2 |
b2 |
n2 |
|
|
|
... |
... |
... |
|
|
|
as |
bs |
ns |
|
|
|
в которой ni – частота интервала (ai ,bi ), i = 1, 2, ..., s. Поскольку интервалы группировки не пересекаются и покрывают все значения признака, сумма интервальных частот равна объему совокупности, ∑si=1 ni = n. Обозначим середину i-го интервала группировки через xi =
К эмпирическим интервальным характеристикам относятся:
интервальное среднее x¯ = 1n ∑si=1 xi ni ,
интервальная дисперсия D (X ) = 1n ∑si=1 (xi − x¯ )2ni ,
интервальное стандартное отклонение σ (X ) = √D (X ).
Отметим, что эти и другие эмпирические интервальные характеристики вычисляются как характеристики
интервального распределения
11 |
12 |

X |
x1 |
x2 |
... |
xs |
|
P |
n1 |
n2 |
... |
ns |
|
n |
n |
n |
|||
|
|
В типичном случае, когда концы интервалов группировки i = (ai ,bi ) образуют арифметическую прогрессию с шагом h,
1 = (a1 , a1 + h), 2 = (a1 + h, a1 + 2h), ...
для приближенного вычисления эмпирической дисперсии σ 2 по интервальному распределению применяется поправка Шеппарда:
σ 2 ≈ σ 2 − 1 h2 .
12
§4. Повторные и бесповторные выборки
Определение. Совокупность, из которой извлекаются элементы, называется генеральной, тогда как совокупность, образованная отобранными элементами, называется выборочной.
Повторной выборкой называется совокупность, образованная по следующей схеме: сначала из генеральной совокупности случайным равновероятным образом извлекается один элемент; затем этот элемент возвращается в генеральную совокупность и все повторяется, пока не будет отобрано необходимое число элементов. Бесповторной выборкой называется совокупность, образованная по аналогичной схеме, но с одним отличием – отобранные элементы в генеральную совокупность не возвращаются.
Характерной особенностью бесповторной выборки является то, что она состоит из различных элементов. Напротив, в состав повторной выборки могут входить одинаковые элементы генеральной совокупности.
Предположим, что из генеральной совокупности Ω объема N извлекается выборка Ωˆ объема n. Пусть X – некоторый признак на Ω . Поскольку все элементы Ωˆ , независимо от вида выборки, являются также элементами Ω , признак X определен и на совокупности Ωˆ .
Обозначим x01 , x02 , ..., x0N значения признака X в генеральной совокупности и X1 , X2 , ..., Xn – значения X в выборке. Далее значения x01, ..., x0N рассматриваются как числа, а X1, ..., Xn – как случайные величины.
Определение. Генеральными (соответственно выборочными) характеристиками признака X называют эмпирические характеристики признака X в генеральной (соответственно выборочной) совокупности.
Например:
x¯0 = |
1 |
(x01 |
+ ... + x0N )– генеральное среднее (число); |
|||||
|
|
|||||||
N |
||||||||
¯ |
1 |
(X1 + ... + Xn)– выборочное среднее (случайная |
||||||
X = |
|
|||||||
|
n |
|
||||||
величина); |
||||||||
|
|
|
|
1 |
|
N |
||
D (X ) = |
|
∑ (x0i − x¯0)2– генеральная дисперсия (число); |
||||||
N |
||||||||
|
|
|
|
|
|
|
i=1 |
|
|
1 |
|
|
n |
||||
ˆ |
|
|
|
|
|
|
¯ 2 |
|
D (X ) = n ∑i=1 (Xi − X ) – выборочная дисперсия (случайная величина).
Теорема. Пусть X1, ..., Xn – значения признака X в выборке, x¯0 – генеральное среднее, а D (X ) – генеральная дис-
¯ |
имеем: |
персия. Тогда для выборочного среднего X |
|
• в случае повторной или бесповторной выборки |
|
¯ |
(8) |
E (X ) = x¯0 ; |
|
13 |
14 |
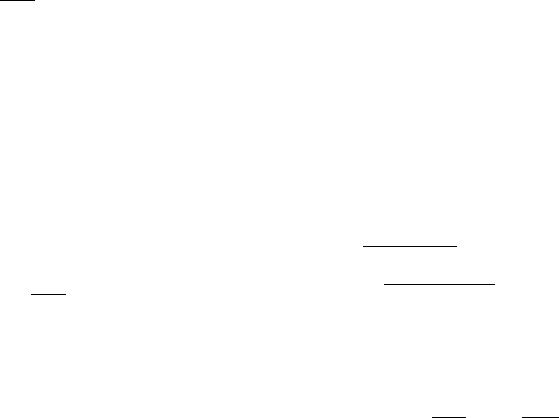
• в случае повторной выборки |
|
|
||||||
¯ |
|
D (X ) |
|
(9) |
||||
D (X ) = |
|
|
|
|
; |
|
||
|
|
|
|
|
||||
|
|
|
n |
|
|
|||
• в случае бесповторной выборки |
|
|
||||||
D (X¯ ) = |
D (X ) |
|
N − n |
, |
(10) |
|||
|
N − 1 |
|||||||
|
n |
|
|
|
|
|||
где N – объем генеральной совокупности.
Из теоремы нетрудно получить следующее следствие:
Следствие. Пусть X1 ,... Xn ; Y1 ,... ,Yn – значения признаков X и Y в выборочной совокупности объема n, COV(X ,Y )
– ковариация признаков X и Y в генеральной совокупности объема N . Тогда для ковариации выборочных сред-
них справедливы соотношения: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
• в случае повторной выборки |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
¯ |
¯ |
|
|
COV(X ,Y ) |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
COV(X ,Y ) = |
|
|
|
|
|
|
|
|
; |
|
|
|
|
(11) |
||||||
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
• в случае бесповторной выборки |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
COV(X¯ ,Y¯ ) = |
COV(X ,Y ) |
|
· |
|
N − n |
. |
|
|
(12) |
||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
N |
− |
1 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Доказательство. Действительно, |
с |
|
учетом |
равенства |
|||||||||||||||||||||||
|
¯ |
¯ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
X ±Y = X |
±Y в случае повторной выборки имеем |
||||||||||||||||||||||||||
|
|
|
OV( ¯ ¯ ) = |
1 |
|
¯ ¯ |
|
|
|
|
¯ |
|
¯ |
|
= |
||||||||||||
|
|
C |
1 |
|
X ,Y |
4 |
D |
X + Y − D X |
−Y |
|
|
|
|||||||||||||||
|
|
|
|
1 |
|
|
− |
|
|
|
− |
|
|
|
|
|
COV(X ,Y ) |
|
|||||||||
|
|
= |
|
4 |
|
D X + Y |
D X |
|
Y |
|
|
= |
|
|
|
|
|
|
|
||||||||
|
|
= |
|
(D (X + Y ) − D (X −Y )) = |
|
|
|
|
|
|
|
. |
|||||||||||||||
|
|
4n |
|
|
|
|
n |
|
|
||||||||||||||||||
Для бесповторной выборки доказательство аналогично. 
Пример 3. Признак X (k) задан на множестве Ω = {1,2,... ,10} следующей таблицей:
k |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
|
|
|
|
|
|
|
|
|
X (k) |
2 |
1 |
1 |
2 |
1 |
2 |
2 |
3 |
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
Из Ω извлекается случайная бесповторная выборка объема 5. Найдите математическое ожидание и диспер-
сию среднего значения ¯ признака в выборке.
X X
Решение. Распределение частот признака X имеет следующий вид
xi |
1 |
2 |
3 |
|
|
|
|
ni |
3 |
6 |
1 |
|
|
|
|
Объем генеральной совокупности N = 10. Найдем генеральное среднее и генеральную дисперсию признака X
x¯0 = |
1 · 3 + 2 · 6 + 3 · 1 |
= |
9 |
= 1,8; |
|
|
|
|||
|
5 |
|
|
|
||||||
|
|
10 |
|
|
|
|
|
|
|
|
D (X ) = |
12 · 3 + 22 · 6 + 32 · 1 |
− |
(x¯ )2 |
= |
9 |
= 0,36. |
||||
|
25 |
|||||||||
|
|
10 |
|
|
|
0 |
|
|
||
Используя формулы (8) и (10) в случае бесповторной выборки объема n = 5, находим математическое ожидание и
|
|
|
|
|
|
|
¯ |
признака X в выборке |
||||||
дисперсию среднего значения X |
||||||||||||||
¯ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E (X ) = x¯0 = 1,8; |
|
|
|
|
|
|
|
|
|
|
|
|||
D (X¯ ) = |
D (X ) |
|
N − n |
= |
|
0,36 |
|
10 − 5 |
= 0,04. |
|||||
|
|
|
|
|||||||||||
|
n N |
− |
1 |
|
|
|
5 · 10 |
− |
1 |
|
||||
|
|
|
|
|
|
|
||||||||
Ответ: 1,8; 0,04.
Пример 4. Признак X (k) задан на множестве Ω = {1,2,... ,10} следующей таблицей:
15 |
16 |

k |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
|
|
|
|
|
|
|
|
|
X (k) |
3 |
3 |
3 |
3 |
1 |
3 |
3 |
2 |
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
Из Ω извлекается случайная повторная выборка объема 5. Найдите математическое ожидание и диспер-
сию среднего значения ¯ признака в выборке.
X X
Решение. Отличие от предыдущего примера состоит в том, что теперь извлекается повторная выборка. Здесь N = 10, n = 5. Генеральные характеристики признака X соответственно равны x¯0 = 2,4, D (X ) = 0,64. Используя формулы
(8) и (9) в случае повторной выборки, находим
¯ |
= 2,4; |
¯ |
D (X ) |
|
0,64 |
= 0,128. |
E (X ) = x¯0 |
D (X ) = |
n |
= |
5 |
||
|
|
|
|
|
Ответ: 2,4; 0,128.
Пример 5. Итоговое распределение баллов на некотором письменном экзамене задано таблицей
Оценка работы |
2 |
3 |
4 |
5 |
|
|
|
|
|
Число работ |
16 |
16 |
24 |
40 |
|
|
|
|
|
Работы проверяли 8 преподавателей, которые раздели-
ли все работы между собой поровну случайным образом. Предполагая независимость оценки от личности проверяющего, найдите математическое ожидание и дисперсию среднего балла по результатам одного преподавателя.
Решение. Объем генеральной совокупности составляет N = 16 + 16 + 24 + 40 = 96 работ. Найдем генеральные характеристики (генеральное среднее x¯0 и генеральную диспер-
17
сию D (X )) признака X (в данном случае оценки): |
|
|||||||||||||||
x¯ |
= |
2 · 16 + 3 · 16 + 4 · 24 + 5 · 40 |
= |
47 |
≈ |
3,917; |
|
|||||||||
|
|
|||||||||||||||
0 |
|
|
|
|
|
|
|
96 |
12 |
|
|
|
||||
D (X ) = |
22 · 16 + 32 · 16 + 42 · 24 + 52 · 40 |
− |
(x¯0 )2 |
= |
||||||||||||
|
|
|
|
|
|
|
|
96 |
|
|
|
|
|
|||
= |
12 |
− |
12 |
|
2 |
= 144 |
≈ 1,243. |
|
|
|
|
|||||
|
|
|
|
|
||||||||||||
|
199 |
|
|
47 |
|
|
|
179 |
|
|
|
|
|
|
|
|
Каждому преподавателю досталось 12 работ. Используя формулы (8) и (10) в случае бесповторной выборки объема n = 12, находим математическое ожидание и дисперсию среднего бала по результатам одного преподавателя
¯ |
47 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E (X ) = x¯0 = 12 ≈ 3,917; |
|
|
|
|
|
|
|
|
|
|
|||||||||
D (X¯ ) = |
D (X ) |
|
N − n |
= |
179 |
· |
96 − 12 |
= |
1 253 |
≈ |
0,0916. |
||||||||
|
|
|
· |
|
|
|
|||||||||||||
|
n N |
− |
1 |
|
144 |
12 |
96 |
− |
1 |
|
13 680 |
|
|||||||
|
|
|
|
|
|
|
|||||||||||||
Ответ: 3,917; 0,01916.
Пример 6. Две игральные кости, красная и синяя, подбрасываются до тех пор, пока не выпадет 19 различных с учетом цвета комбинаций очков. Пусть Si – сумма оч-
ков на красной и синей кости в -той комбинации, ¯ – i S
среднее арифметическое всех этих сумм, i = 1,... ,19. Най-
дите математическое ожидание и дисперсию среднего
значения ¯.
S
Решение. Генеральную совокупность объема N = 36 можно представить как пространство элементарных исходов в опыте по подбрасыванию двух игральных костей, выборочную – объема n = 19 – как результат бесповторной выборки из этой генеральной совокупности. В обеих совокупностях определены признаки: X1 – число очков на красной, X2 – число очков на синей игральной кости и
18
