
Образцы решения экзаменационных задач III
.docТрехмерные задачи оптимизации портфелей в моделях Тобина
Рынок состоит из двух рисковых активов A1, A2 и одного безрискового A0. Параметры рынка
Безрисковая доходность m0,
вектор ожидаемых доходностей рисковых
активов - m =![]() (m1
m2) и матрица
ковариации рисковых активов C
=
(m1
m2) и матрица
ковариации рисковых активов C
=
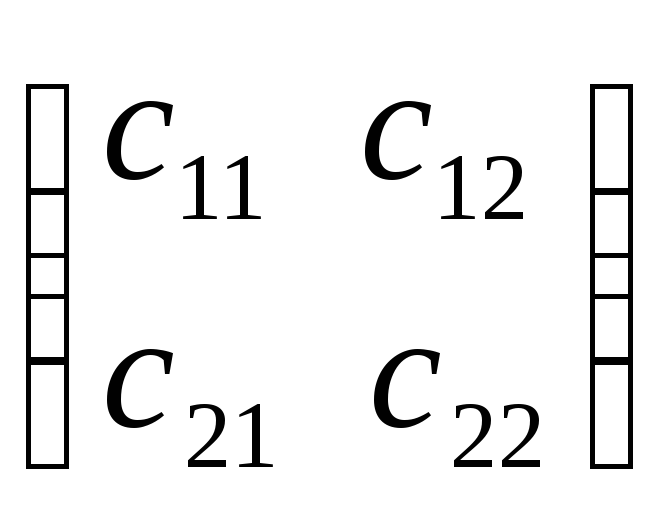 .
.
где веса x1 и x2 любые вещественные числа. Полный вектор m ожидаемых доходностей
m =
Полная матрица ковариаций С:

Портфель и его характеристики. Портфель задается полным вектором весов х:
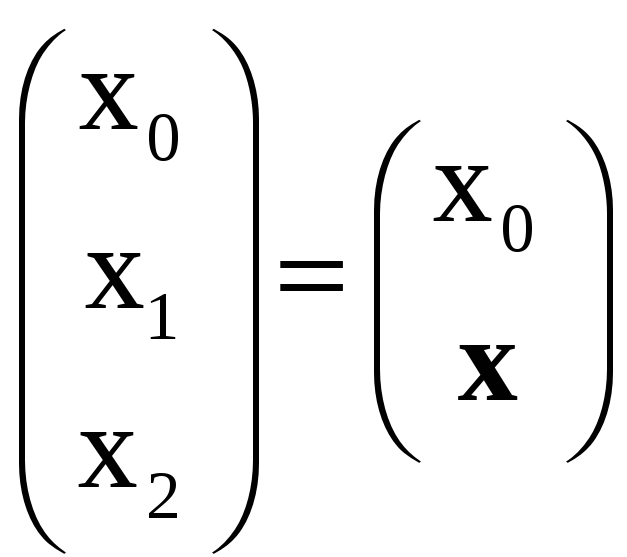
x0 +x1 + x2 = 1
где
x =![]()
- рисковая часть портфеля.
Ожидаемая доходность портфеля есть (учитывая, что х0 =1- x1 - x2)
E[x] = (m, x) = m0x0 + m1x1 + m2x2 = m0 +(m1-m0)x1+(m2-m0)x2 = m0+(m0,x)
где
m0=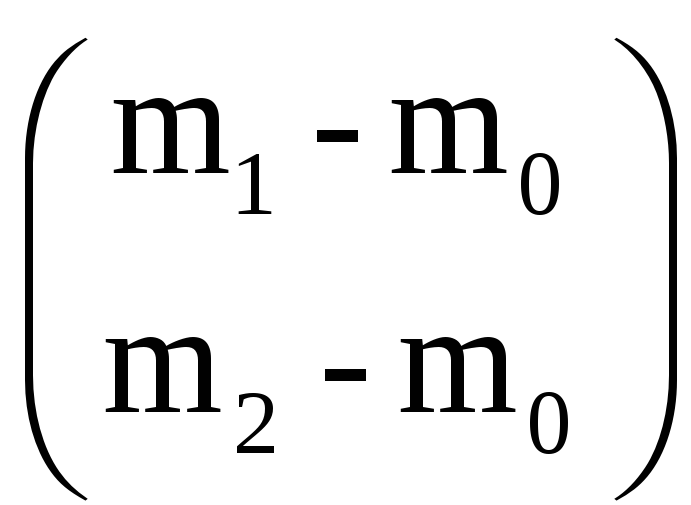
Риск (вариация) есть
V[x] = (Сx, x) = (Сx, x) = c11 (x1)2 + c22 (x2)2 + 2c12x1x2,
Полезность портфеля
U[x] = E[x] – (/2)V[x] = (m0,x) - (/2)(Сx, x) =
= m0 +(m1-m0)x1+(m2-m0)x2 -(/2)(c11∙x12 + c22 ∙ x2 2 +2c12 x1x2)
Таким образом, характеристики портфеля зависят только от рисковой части портфеля, что существенно упрощает задачи оптимизации портфелей, поскольку эти задачи становятся задачами безусловной оптимизации.
Задача 1.
Заданы следующие параметры рынка из трех активов А0 , А1, А2.
|
m0 = |
1 |
c11 = |
2 |
|
m1 = |
2 |
c22 = |
4 |
|
m2 = |
3 |
c12 = |
-1 |
Найти портфель с максимальной полезностью в модели Тобина, для инвестора с
коэффициентом неприятия риска равным = 2.
Решение. Задача состоит в нахождении безусловного максимума функции полезности
U[x] = E[x] – (/2)V[x] = (m0,x) - (/2)(Сx, x) =
= m0 + (m1-m0)x1+(m2-m0)x2 -(/2)(c11∙x12 + c22 ∙ x2 2 +2c12 x1x2)= x1-2x2-(2x12 + 4 x2 2-2x1x2).
Дифференцируя и приравнивая частные производные по x1 и x2 нулю получим систему уравнений
|
4х1 - 2х2 =1 |
|
-1х1 + 4х2 =1 |
Решая ее получим
х1 = 0,4286; х2 = 0,3571 и х0 =1- x1 - x2 = 0,2143.
Задача 2.
Заданы следующие параметры рынка из трех активов А0, А1, А2.
|
m0 = |
1 |
c11 = |
2 |
|
m1 = |
2 |
c22 = |
4 |
|
m2 = |
3 |
c12 = |
-1 |
Найти касательный портфель в модели Тобина:
Решение. Касательный портфель = (0;1;2) – эффективный чисто рисковый (0= 0) портфель,
который получается из рисковой части х = (х1; х2) любого оптимального (эффективного) портфеля х = (х0;х1;х2) путем ее нормирования, чтобы рисковая часть стала портфелем:
0 = 0; 1 = х1/(x1+х2) = х1/(1-х0); 2 = х2/(x1+х2) = х2/(1-х0);
Взяв в качестве исходного например портфель из предыдущей задачи получим касательный портфель:
0 = 0; 1 = х1/(1-х0) = 0,4286/0,2143= 0,545; 2 = х2/(1-х0) = 0,3571/0,2143= 0,455;
Задача 3.
Заданы следующие параметры рынка из трех активов А0 , А1, А2.
|
m0 = |
1 |
c11 = |
2 |
|
m1 = |
2 |
c22 = |
4 |
|
m2 = |
3 |
c12 = |
-1 |
Найдите уравнение эффективной границы - прямой E = a1 +a0 на плоскости
риск-доходность (E) в модели Тобина
Решение. Для решения этой задачи необходимо знать характеристики касательного портфеля.
Из предыдущей задачи имеем
m = m11 +m22 =1·0,545 + 2·0,455 = 2,45
V =212 + 422 - 212 =2·0,5452 + 4·0,4552 _ 2·0,545·0,455 = 0,9256
σ =0,9621.
Тогда в уравнении E = a1 +a0 коэффициенты имеют вид
a0 = m0 = 1; a1m - m0)/σ = 1,51
Задача 4.
Заданы следующие параметры рынка из трех активов А0 , А1, А2.
|
m0 = |
1 |
c11 = |
2 |
|
m1 = |
2 |
c22 = |
4 |
|
m2 = |
3 |
c12 = |
-1 |
Найти портфель с минимальным риском, доходность которого не меньше Е0 = 2,00
в модели Тобина.
Решение. Задача сводится к минимизации риска
V[x] = (Сx, x) = c11 (x1)2 + c22 (x2)2 + 2c12x1x2 = 2x12 + 4x2 2-2x1x2
при условии
E[x] = (m0,x) =(m1-m0)x1 + (m2-m0)x2 = 1+x1 + 2x2 ≥ 2
Поскольку требуемая доходность Е0 = 2,00 больше безрисковой m0 =1, то неравенство
можно заменить на равенство и задача примет вид
V[x] = (Сx, x) = 2x12 + 4x2 2 - 2x1x2→ min
при условии
(m0,x) = x1 + 2x2 = 1
Выражая
x1 = 1-2x2=1- 2x2
и подставляя в выражение для риска получим
V[x]= 2·(1- 2x2)2 + 4x22- 2(1-2x2)x2 = 2-8x2+8x22 +4x22 -2x2 + 4x22 =16x22 -10x2 +2.
Дифференцируя V[x]= V[x2] по x2 и приравнивая производную V´[x2] к нулю получим
V´[x2] = 32x2 -10 = 0,
откуда x2 =5/16; x1 = 1-2x2 = 6/16; х0 =1- x1 - x2 = 5/16.
Задача 5.
Заданы следующие параметры рынка из трех активов А0 , А1, А2.
|
m0 = |
1 |
c11 = |
2 |
|
m1 = |
2 |
c22 = |
4 |
|
m2 = |
3 |
c12 = |
-1 |
Найти портфель с максимальной доходностью риск (стандартное отклонение) которого не
больше заданного 0 = 2 в модели Тобина.
Решение. Задача сводится к максимизации доходности
E[x] = m0 +(m0,x) = m0 + (m1-m0)x1 + (m2-m0)x2 = 1+x1 + 2x2
при условии
V[x] = (Сx, x) = c11 (x1)2 + c22 (x2)2 + 2c12x1x2 ≤ 02 или
2x12 + 4x2 2-2x1x2 ≤
Поскольку предельный риск положителен, то неравенство можно заменить на равенство
и задача примет вид
1+x1 + 2x2 → max
при условии
2x12 + 4x2 2-2x1x2 =
Лучше всего решать эту задачу методом множителей Лагранжа. Функция Лагранжа имеет вид
L[x] = m0 +(m0,x) - μ(Сx, x)
Тогда соответствующая система уравнений будет иметь вид:
m0 - μСx= 0, (Сx, x)=4
Откуда получаем
x=(1/μ)С-1m0
Тогда из второго равенства получим
(Сx, x)= (1/μ2)(С-1m0,m0) = 4
Поскольку

то
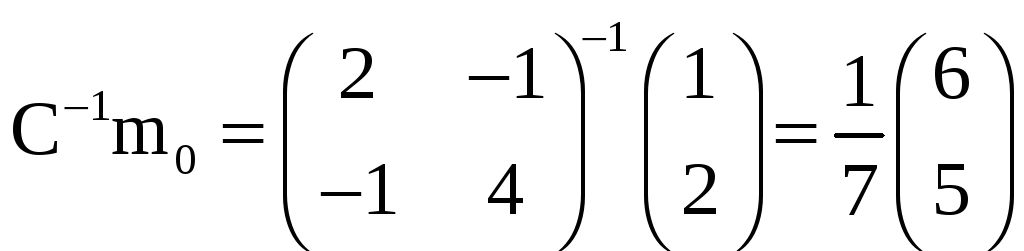
и
(С-1m0,m0) = 16/7
Тогда из уравнения
(1/μ2)(С-1m0,m0) = 4
получим
1/μ2 = 4/(16/7)=7/4 и 1/μ = 7/2
и
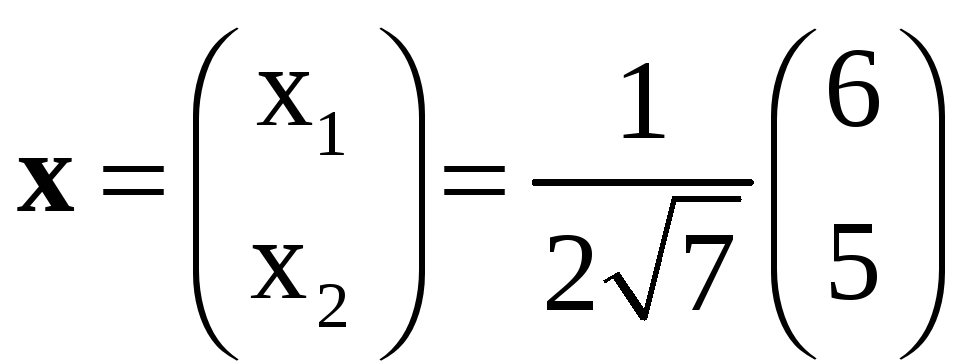
|
x0=0,703028 |
|
x1=0,161985 |
|
x2=0,134987 |
