
- •Федеральное государственное образовательное бюджетное
- •1 Линейное программирование
- •Контрольные вопросы и упражнения
- •2 Различные формы записи задач линейного программирования. Приведение задачи к каноническому виду
- •3 Графический метод решения злп
- •Контрольные вопросы и упражнения
- •4 Симплекс-метод решения задач линейного программирования с естественным базисом
- •Контрольные вопросы и упражнения
- •5 Симплекс-метод с искусственным базисом
- •Контрольные вопросы и упражнения
- •6 Двойственность в линейном программировании
- •Контрольные вопросы и упражнения
- •7 Технология решения задач линейного программирования с помощью надстройки поиск решения в среде excel
- •Список литературы
- •Задания для самостоятельной работы
Контрольные вопросы и упражнения
1. В какой из точек
построенной области допустимых решений
на рисунке 5 функция
![]() достигает максимального и минимального
значения?
достигает максимального и минимального
значения?

Рисунок 5
2. В какой из точек
области
![]() допустимых решений на рисунке 6 функция
допустимых решений на рисунке 6 функция![]() достигает максимального и минимального
значения?
достигает максимального и минимального
значения?

Рисунок 6
3. Построить область
допустимых решений неравенства
![]() .
.
4. Каковы координаты
градиента функции (вектора
![]() )
в следующей задаче линейного
программирования:
)
в следующей задаче линейного
программирования:

5. При решении
задачи линейного программирования
получили область допустимых решений
(рис.7). Найти максимальное значение
функции
![]() .
.

Рисунок 7
6. Построить линию
нулевого уровня
![]() ,
соответствующую целевой функции
,
соответствующую целевой функции![]() .
.
7 .
Построить область допустимых решений
задачи линейного программирования:
.
Построить область допустимых решений
задачи линейного программирования:
8.Решить графическим методом задачи N№ 2, 3 из пункта 1.
9. Решить графическим методом задачи ЛП:


4 Симплекс-метод решения задач линейного программирования с естественным базисом
Для решения задач
ЛП существует универсальный метод –
метод последовательного улучшения
плана или симплекс-метод, который состоит
из двух вычислительных процедур:
симплекс-метода с естественным базисом
и симплекс-метода с искусственным
базисом. Выбор конкретной процедуры
осуществляется после приведения исходной
задачи линейного программирования к
каноническому виду. В теории линейного
программирования показано, что оптимальное
решение связано с угловыми точками
многогранника решений, которым отвечают
опорные планы (неотрицательные базисные
решения системы уравнений канонической
задачи ЛП). Каждый из опорных планов
определяется системой m
линейно независимых векторов, содержащихся
в данной системе из n
векторов. Верхняя граница количества
опорных планов, содержащихся в данной
задаче, определяется числом сочетаний
![]() .
.
Пример. Решить задачу линейного программирования.

Решение: Приведем задачу к каноническому виду путем введения дополнительных переменных

Найдем все базисные решения, исходя из того, что система ограничений состоит из двух уравнений с четырьмя переменными. Последовательно придавая двум переменным значения, равные нулю, получаем:

Среди этих базисных решений четыре опорных, удовлетворяющих условию неотрицательности:

Согласно теории линейного программирования оптимальное решение содержится среди опорных планов, значит:

Максимальное
значение, равное 375, достигается на
опорном плане
![]() ,
т.е. оптимальное решение
,
т.е. оптимальное решение![]() .
.
Очевидно, что при больших m и n найти оптимальный план, перебирая указанным способом все опорные планы, весьма затруднительно, поэтому применяют определенную схему, называемую симплекс-методом.
Алгоритм симплекс-метода с естественным базисом:
ШАГ 1. Приведение задачи к каноническому виду, притом все элементы столбца свободных членов должны быть не отрицательны.
ШАГ 2. Нахождение начального опорного решения. Путем элементарных алгебраических преобразований, включающих умножение правой и левой частей уравнений на одно и то же число и их сложение задача (1) приобретает предпочтительный вид
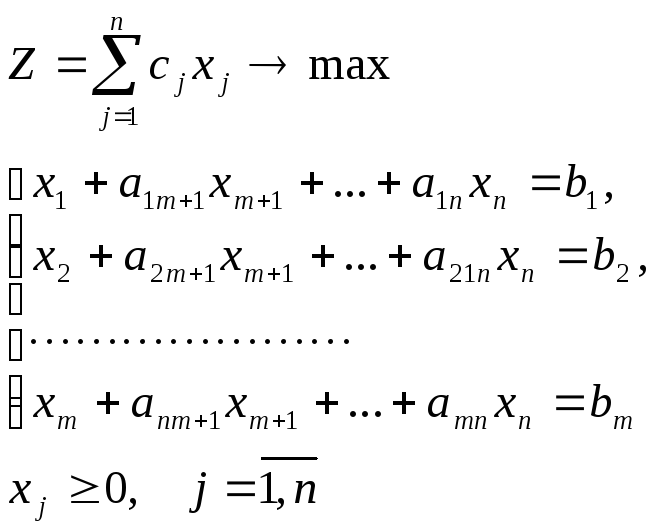 (3)
(3)
Выбираем m
переменных,
называемых базисными (БП) и обладающих
свойством: они входят с коэффициентом
1
только в одно уравнение и с коэффициентом
0
в остальные уравнения системы (3).
Остальные n-m
переменных называются свободными. Все
свободные переменные полагаются равными
0,
а базисные переменные – равным правым
частям соответствующих ограничений
системы. Пусть m
базисных
переменных – это переменные
![]() .
Тогда начальное решение
.
Тогда начальное решение![]() имеет вид:
имеет вид:
![]()
ШАГ 3.
Целевая функция выражается через
свободные переменные и максимизируется.
Для этого базисные переменные выразим
из системы ограничений через свободные
![]() и подставим в выражение функцииZ
. Получим приведенные коэффициенты
целевой функции
и подставим в выражение функцииZ
. Получим приведенные коэффициенты
целевой функции
![]() .
.
ШАГ 4.
Проверка плана на оптимальность. Составим
исходную симплекс-таблицу, записывая
приведенные коэффициенты целевой
функции в Z-строку
с противоположными знаками, а константу
![]() со своим знаком.
со своим знаком.
Таблица 4 – Исходный вид симплекс-таблиц
|
БП |
СП |
Коэффициенты при переменных |
Q | ||||||||
|
x1 |
x2 |
… |
xm |
xm+1 |
… |
xm+k |
… |
xn | |||
|
x1 |
b1 |
1 |
0 |
… |
0 |
a1,m+1 |
… |
a1,m+k |
… |
a1n |
|
|
x2 |
b2 |
0 |
1 |
… |
0 |
a2,m+1 |
… |
a2,m+k |
… |
a2n |
|
|
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
|
|
xq |
bq |
0 |
0 |
… |
0 |
aq,m+1 |
… |
aq,m+k |
… |
aqn |
|
|
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
|
|
xm |
bm |
0 |
0 |
… |
1 |
am,m+1 |
… |
am,m+k |
… |
amn |
|
|
Z |
Z0 |
0 |
0 |
… |
0 |
|
… |
|
… |
|
|
1. Если в Z-
строке симплекс-таблицы, содержащей
некоторый опорный план, нет отрицательных
элементов (не считая
![]() ),
то данный план оптимален и задача решена.
К тому же, если вZ-
строке симплексной таблицы, содержащей
оптимальный план, нет нулевых элементов
(не считая
),
то данный план оптимален и задача решена.
К тому же, если вZ-
строке симплексной таблицы, содержащей
оптимальный план, нет нулевых элементов
(не считая
![]() и элементов, соответствующих базису),
то оптимальный план единственный. Если
же вZ-
строке последней симплексной таблицы,
содержащей оптимальный план, есть хотя
один нулевой элемент, соответствующий
свободной переменной, то ЗЛП имеет
бесконечное множество решений.
и элементов, соответствующих базису),
то оптимальный план единственный. Если
же вZ-
строке последней симплексной таблицы,
содержащей оптимальный план, есть хотя
один нулевой элемент, соответствующий
свободной переменной, то ЗЛП имеет
бесконечное множество решений.
2. Если в Z-
строке есть хотя бы один отрицательный
элемент (не считая
![]() ),
а в любом столбце с таким элементом есть
хотя бы один положительный, то можно
перейти к новому опорному плану, более
близкому к оптимальному. Для этого
столбец с отрицательным элементом
),
а в любом столбце с таким элементом есть
хотя бы один положительный, то можно
перейти к новому опорному плану, более
близкому к оптимальному. Для этого
столбец с отрицательным элементом![]() вZ-
строке берут за разрешающий (если в Z-
строке отрицательных элементов несколько,
то за разрешающий выбирают столбец с
наименьшим элементом). Следовательно,
столбец с номером m+
k
станет ведущим
или разрешающим
и переменная
вZ-
строке берут за разрешающий (если в Z-
строке отрицательных элементов несколько,
то за разрешающий выбирают столбец с
наименьшим элементом). Следовательно,
столбец с номером m+
k
станет ведущим
или разрешающим
и переменная
![]() будет включена в базис.
будет включена в базис.
3. Среди элементов
ведущего столбца находят положительные.
Если таковых нет, то задача не имеет
решений в силу неограниченности целевой
функции (![]() ).
).
4. Для положительных
элементов аi,m+k
подсчитывают
симплексные отношения (отношения
свободных членов к соответствующим
положительным элементам ведущего
столбца)
![]() ,
и выбирают среди них наименьшее. Пусть
минимальное симплексное отношение
будет в строкеq.
Строка с
номером q
станет ведущей (разрешающей), а элемент
аq,m+k
– ведущим.
Переменная xq
выйдет
из базиса.
,
и выбирают среди них наименьшее. Пусть
минимальное симплексное отношение
будет в строкеq.
Строка с
номером q
станет ведущей (разрешающей), а элемент
аq,m+k
– ведущим.
Переменная xq
выйдет
из базиса.
5. Выполнят одну итерацию по замещению базисной переменной методом Жордана - Гаусса. Строят новую симплексную таблицу и переходят к первому пункту.
Рассмотрим симплекс-метод и метод замещения Жордана – Гаусса на примере.
Пример. Предприятие изготавливает три вида продукции, при этом используется три вида сырья. Нормы расхода каждого сырья на 1 ед. продукции определенного вида приведены в таблице 5. Известны запасы этого сырья, а также прибыль, получаемая при реализации единицы продукции каждого вида.
Таблица 5 – Нормы расходы сырья и получаемая прибыль
|
|
А |
В |
С |
Запасы сырья, ед. |
|
І |
- |
1 |
1 |
12 |
|
ІІ |
1 |
3 |
2 |
18 |
|
ІІІ |
- |
1 |
2 |
16 |
|
Прибыль, ден.ед. |
2 |
7 |
6 |
|
Сколько единиц продукции каждого вида следует выпускать предприятию для получения максимальной прибыли при условии, что сырье второго вида будет израсходовано полностью.
Решение:
Составим математическую модель задачи.
Обозначим через
![]() -
количество выпускаемой продукции.
Область допустимых решений имеет вид
-
количество выпускаемой продукции.
Область допустимых решений имеет вид

Согласно условиям задачи предприятие должно получить максимальную прибыль, следовательно, целевая функция выразится формулой
![]()
Приведем задачу к каноническому виду
![]()

В
 ыразим
базисные переменные
ыразим
базисные переменные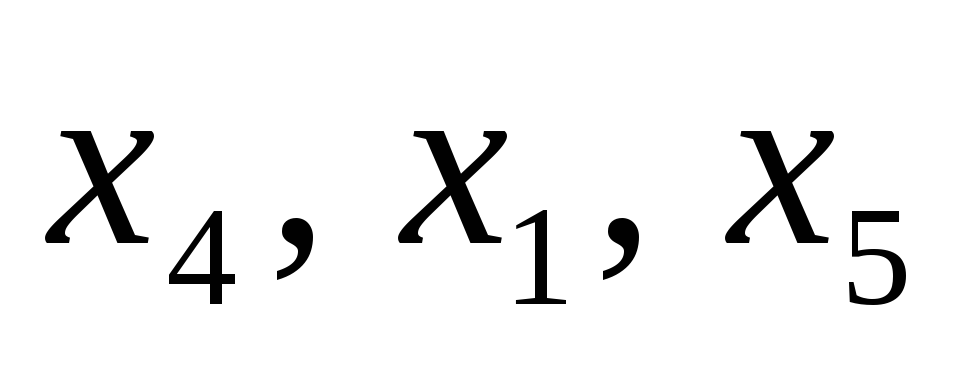 и целевую функцию через свободные
переменные:
и целевую функцию через свободные
переменные:
![]()
Найдем начальный опорный план задачи
![]()
Занесем коэффициенты целевой функции и системы ограничений в симплексную таблицу
Таблица 6 – Исходная симплекс-таблица
|
БП |
СЧ |
х1 |
х2 |
х3 |
х4 |
х5 |
Q |
|
х4 |
12 |
0 |
1 |
1 |
1 |
0 |
12 |
|
х1 |
18 |
1 |
3 |
2 |
0 |
0 |
9 |
|
х5 |
16 |
0 |
1 |
2 |
0 |
1 |
8 |
|
Z |
36 |
0 |
-1 |
-2 |
0 |
0 |
|
В Z- строке есть отрицательные элементы. Следовательно, начальный опорный план не является оптимальным. Найдем минимальный отрицательный элемент Z- строки: (-2) в столбце «х3». За ведущий столбец выбираем «х3», значит, переменная х3 будет включена в базис.
Так как среди
элементов ведущего столбца есть
положительные, то существует новый
опорный план, более близкий к оптимальному.
Подсчитаем симплексные отношения
(отношения свободных членов к
соответствующим положительным элементам
ведущего столбца) и найдем среди них
минимальное:
![]() .
Значит, 3-я строка является ведущей, а
элемента33
= 2 – разрешающим. Следовательно,
переменная х5
выйдет из базиса.
.
Значит, 3-я строка является ведущей, а
элемента33
= 2 – разрешающим. Следовательно,
переменная х5
выйдет из базиса.
Методом Жордана – Гаусса проведем одну итерацию замещения.
Таблица 7 – Одно из оптимальных решений
|
БП |
СЧ |
х1 |
х2 |
х3 |
х4 |
х5 |
Q |
|
х4 |
4 |
0 |
½ |
0 |
1 |
-½ |
8 |
|
х1 |
2 |
1 |
2 |
0 |
0 |
0 |
1 |
|
х3 |
8 |
0 |
½ |
1 |
0 |
½ |
16 |
|
Z |
52 |
0 |
0 |
0 |
0 |
1 |
|
Так как в Z-
строке все элементы больше или равны
нулю, то найден оптимальный план:
![]() .
.
Он не единственный, так как существует нулевой элемент Z- строки, соответствующий свободной переменной х2.
Найдем второе оптимальное решение. Столбец «х2» принимаем за ведущий и находим минимальное симплексное отношение:
 .
Тогда вторая строка станет ведущей.
.
Тогда вторая строка станет ведущей.
Таблица 8 – Второе оптимальное решение
|
БП |
СЧ |
х1 |
х2 |
х3 |
х4 |
х5 |
Q |
|
х4 |
3,5 |
-½ |
0 |
0 |
1 |
-½ |
|
|
х2 |
1 |
½ |
1 |
0 |
0 |
0 |
|
|
х3 |
7,5 |
-½ |
0 |
1 |
0 |
½ |
|
|
Z |
52 |
0 |
0 |
0 |
0 |
1 |
|
Из последней таблицы
![]() ,
,
но данное решение не отвечает условию целочисленности.
