Физика_Л_3-4

Семестр 4. Лекции 3-4.

Лекции 3 - 4. Волновые свойства микрочастиц.

Гипотеза де Бройля. Дифракция микрочастиц. Принцип неопределённости Гейзенберга. Задание состояния микрочастицы. Волновая функция, ее статистический смысл и условия, которым она должна удовлетворять. Принцип суперпозиции квантовых состояний. Общее уравнение Шредингера. Уравнение Шредингера для стационарных состояний.

Гипотеза де Бройля

В 1924 году французский физик Луи де Бройль высказал гипотезу о том, что все мате-

риальные объекты в природе обладают как корпускулярными, так и волновыми свойства-

ми. По гипотезе де Бройля корпускулярно-волновой дуализм является всеобщим свойством материи, и поэтому любая частица (электрон, протон, нейтрон и др.) обладает волновыми свой-

ствами. При этом наличие у частицы волновых свойств принципиально изменяет характер её движения и способ описания такого движения.

По гипотезе де Бройля волновые свойства свободной частицы, движущейся по инер-

ции в отсутствие внешних силовых полей, описывает плоская волна де Бройля, частота и

Направление распространения волны де Бройля совпадает с направлением движения частицы, и можно показать, что групповая скорость волны uгр и скорость частицы одинаковы.

В теории волновых процессов уравнение плоской монохроматической волны, распространяющейся в направлении оси x , имеет вид:

(x,t) Acos( t kx) .

Его часто записывают в комплексной форме:

(x,t) Aexp i( t kx) ,

Бройля можно записать в виде:

(x, t) Aexp i (Et px) .



Плоская волна де Бройля описывает волновые свойства свободной частицы, имею-

щей энергию E и импульс p . Сравнивая квадраты амплитуд волн де Бройля в различных об-

ластях пространства, можно оценить вероятности нахождения частицы в этих областях. Вероятность обнаружения частицы в данной области пространства тем больше, чем больше квадрат амплитуды волны де Бройля, т.е. её интенсивность.

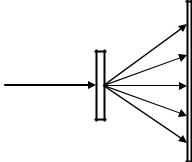
Волны де Бройля, которые часто называют волнами материи, как и волны любой природы, могут отражаться, преломляться, интерферировать друг с другом, испытывать дифракцию при взаимодействии с неоднородностями. Тогда можно говорить, например, о дифракции частиц и наблюдать дифракционные эффекты в различных экспериментах с неоднородными средами. Один из первых опытов по дифракции электронов на кристалле был выполнен в 1927 году американскими учёными Клинтоном Дэвиссоном и Лестером Джермером .

1

Семестр 4. Лекции 3-4.

Опыт Дэвиссона-Джермера.

В опыте Дэвиссона-Джермера ускоренные в электронной пушке электроны попадали на кристалл никеля под некоторым углом скольжения . Регулировкой величины ускоряющей разности потенциалов в электронной пушке изменялись кинетическая энергия и импульс вылетающих электронов и, следовательно, их длина волны де Бройля. По току детектора в опыте измерялось число отражённых от кристалла электронов. Структура кристалла никеля была хорошо известна из данных рентгеноструктурного анализа

Было обнаружено резкое увеличение числа отражённых от кристалла электронов в тех случаях, когда для электронных волн де Бройля выполнялось условие Вульфа-Брэггов, (это условие было получено в опытах по дифракции рентгеновских лучей на кристалле никеля):

соответствующее условию усиления вторичных волн, отражённых от различных атомных слоёв (плоскостей). В этой формуле d - расстояние между атомными плоскостями, проходящими через узлы кристаллической решётки, а целое число n - порядок максимума отражения волны де Бройля. Результаты опыта полностью подтвердили гипотезу де Бройля.

В 1927 году Петр Саввич Тартаковский, а в 1928 году английский физик Дж. Томсон (сын Дж. Томсона, открывшего электрон) получили новое подтверждение гипотезы де Бройля. В своих экспериментах Тартаковский наблюдал дифракционную картину при прохождении медленных электронов через поликристаллы никеля, а Томсон наблюдал дифракционную картину, возникающую при прохождении пучка электронов через тонкую поликристаллическую фольгу из золота.

Опыт Томсона

Фольга

пучок электронов

Фотопластинка

Впоследствии дифракционные явления были обнаружены также для нейтронов, протонов, атомных и молекулярных пучков. Экспериментальное доказательство наличия волновых свойств микрочастиц привело к выводу о том, что это универсальное явление природы, общее свойство материи. Следовательно, волновые свойства должны быть присущи и макроскопическим телам. Однако вследствие большой массы макроскопических тел их волновые свойства не могут быть обнаружены экспериментально. Например, песчинке массой 0,1 г, движущейся со скоростью 0,1 м/с, соответствует волна де Бройля с длиной порядка 10–30 м, т. е. приблизительно на 20 порядков меньше размеров атомов. Такая длина волны лежит за пределами доступной наблюдению области. Этот пример показывает, что макроскопические тела могут проявлять только корпускулярные свойства.

Таким образом, учёт волновых свойств частиц необходим в случае, когда характер-

ный размер задачи сопоставим с длиной волны де Бройля.

Принцип неопределённости Гейзенберга.

Принцип неопределённости, открытый Вернером Гейзенбергом в 1927 г., является одним из фундаментальных принципов квантовой механики.

2

Семестр 4. Лекции 3-4.

В классической физике погрешности измерения параметров частицы обусловлены только точностью измерений. И если физические величины являются независимыми друг от друга, то погрешности их измерений тоже являются независимыми. При указании значений измеренной физической величины приводится доверительный интервал, в котором она принимает значения с некоторой вероятностью. Полуширина этого доверительного интервала пропорциональна среднеквадратичному отклонению.

Оказывается, что учёт волновых свойств частиц накладывает принципиальные ограничения на точность измерения физических величин. Эти ограничения не связаны с погрешностями измерений, а являются следствиями корпускулярно-волнового дуализма частиц.

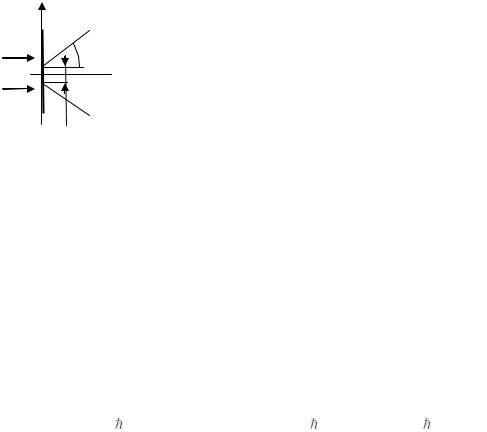
Рассмотрим дифракцию частицы на щели. Частица движется по нормали к экрану со щелью, поэтому её вектор импульса направлен перпендикулярно к экрану. Если вдоль экрана, перпендикулярно щели направить ось Х, то можно сказать, что до щели у частицы был нулевой импульс вдоль оси Х. Пусть ширина щели равна x. После дифракции на щели частицы как волны де Бройля положение первого минимума дифракционной картины задаётся величиной угла , где x sin . Т.е. можно сказать, что после щели у частицы появится дополнитель-

ный импульс вдоль оси Х: px , что приведёт к отклонению частицы от направления первона-

Этот факт отражает принцип неопределённости – в природе не су-

ществует состояния частицы с точно определёнными значениями координаты и проекции импульса на эту ось. Таким образом, понятие траектории частицы в микромире теря-

ет смысл.

Измерение величины одного параметра приводит к изменению величины какого-то другого параметра, следовательно, появляется неопределённость этого параметра. Чтобы отразить этот факт, принцип неопределённости можно сформулировать следующим образом – любое

измерение состояния системы приводит к изменению этого состояния.

Математическим выражением термина неопределённость физической величины является среднеквадратичное отклонение значения этой величины, получаемое в процессе наблюдения за частицей (системой). Это среднеквадратичное отклонение физической величины А принято обозначать А.

Две физические величины называются канонически сопряжёнными, если для них можно записать соотношение неопределённости Гейзенберга. Например, координата частицы и импульс вдоль этой координаты являются канонически сопряжёнными. Тогда для них можно за-

В любом состоянии частицы нельзя одновременно как угодно точно измерить импульс и координату частицы вдоль одной оси.

Замечание. В этих соотношениях неравенство надо понимать как оценочное, т.к. при расчётах получаются оценки по порядку величин.

Но координата и импульс вдоль другой координаты не являются сопряжёнными величинами. Например px y 0 - т.е. эти величины могут быть измерены одновременно как угодно точно.

3

Семестр 4. Лекции 3-4.

Существуют и другие сопряжённые величины. Например, энергия и время: E t 2 ,

где Е – неопределённость значения энергии, t – неопределённость интервала времени, в течение которого проводились наблюдения за значением энергии.

Отсюда, в частности, следует оценка времени пребывания системы в нестабильном со-

стоянии с «избыточным» значением энергии: ~ E .

И, наоборот, если неопределённость времени наблюдения за состоянием системы равнаt , то в этом состоянии неопределённость энергии E ~ t .

Замечание. В случае, когда длина волны де Бройля значительно меньше характерного размера задачи L, можно пользоваться законами классической физики. Действительно, ес-

В итоге, можно сказать, что при учёте волновых свойств частицы теряет смысл не

только понятие траектории, но и деление энергии частицы на потенциальную и кинетическую. Ибо потенциальная энергия зависит от координаты, а кинетическая от импульса.

Волновая функция

Состояние микрочастицы (характеристики её движения, взаимодействия с другими частицами и т.д.) полностью задаётся функцией, которую называют волновой функцией и обозначают (пси-функция).

Переходя к описанию движения частиц в квантовой механике, сформулируем ряд её постулатов, лежащих в основе теории. Первый постулат квантовой механики гласит: состоя-

ние частицы в квантовой механике описывается волновой функцией (x, y, z,t) , являю-

щейся функцией пространственных координат и времени. Физико-математический аппарат,

разработанный в квантовой механике, позволяет, проводя некоторые операции над волновой функцией , получать полную информацию о движении микрочастицы.

Статистический смысл волновой функции.

Невозможность задать состояние микрочастицы указанием в любой момент времени её координат и скорости и отказ от траекторного способа описания движения приводят к вероятностному способу описания движения микрочастицы. Это означает, что в квантовой механике,

описывая состояние микрочастицы, следует указать способ определения вероятности обнаружения частицы в различных точках пространства в данный момент времени.

В 1926г. Макс Борн предложил следующий вероятностный смысл волновой функции: квадрат модуля волновой функции (x, y, z,t) определяет плотность вероятности

обнаружения частицы в момент времени t 0 в точке пространства M M (x, y, z) с координатами x, y, z :

dVdP 2 .

Это соотношение можно преобразовать к виду:

где dP - вероятность того, что для заданного квантового состояния частицы в некоторый момент времени мы обнаружим частицу в некоторой малой области пространства, объём кото-

рой dV, - функция комплексно-сопряжённая функции . Поэтому для нахождения вероят-

4

Следовательно, если частица не может находиться в области V, то P V 2dV 0 .

стица обязательно находится в области V, то P V 2dV 1.

V

Следовательно, квадрат модуля волновой функции должен быть интегрируемой функцией по этой области.

Замечание. Вероятность того, что частица находится в какой-то определённой точке, равна нулю, т.к. в этом случае объём соответствующей области нулевой.

Свойства волновой функции.

Вероятностный смысл волновой функции накладывает определённые ограничения, или условия, на волновые функции в задачах квантовой механики. Эти стандартные условия ча-

сто называют условиями регулярности волновой функции.

1. Условие конечности волновой функции. Волновая функция не может принимать

интеграл выражает условие нормировки волновой функции; волновую функцию,

удовлетворяющую этому условию, называют нормированной волновой функцией. К условию нормировки мы ещё вернёмся. В задачах с нормированной волновой функцией квадрат модуля волновой функции должен стремиться к нулю на бесконечности.

2.Условие однозначности волновой функции. Волновая функция должна быть одно-

значной функцией координат и времени, так как плотность вероятности обнаружения частицы должна определяться в каждой задаче однозначно.

3.Условие непрерывности волновой функции. В любой момент времени волновая функция должна быть непрерывной функцией пространственных координат. Кроме того, непрерывными должны быть также частные производные волновой функции

x , y , z .

Эти условия часто называют для краткости условиями КОН.

Принцип суперпозиции состояний.

Если частица может находиться в одном состоянии и может находиться в другом состоянии, то она может находиться и в состоянии, являющимся суперпозицией этих состояний. Это означает, что если первое состояние описывается волновой функцией 1, а второе - 2, то

состояние, являющееся суперпозицией состояний, описывается волновой функцией, являющейся их линейной комбинацией: 3 = с1 1+с2 2, где с1 и с2 – некоторые константы.

Суперпозиция состояний в квантовой механике отличается от суперпозиции состояний в классической физике. Например, в классической физике суперпозиция колебаний приводит к новому колебанию с большей или меньшей амплитудой. Возможен даже случай нулевой амплитуды. В квантовой механике же нулевая амплитуда соответствует отсутствию частицы в данном состоянии.

5

Семестр 4. Лекции 3-4.

Для того чтобы определить какую-то физическую величину, описывающую состояние частицы, надо осуществить некие математические операции над волновой функцией, соответствующей данному состоянию, и проанализировать полученные результаты.

Процесс определения значения какой-то физической величины А в соответствующем состоянии частицы, по своей сути является процессом измерения данной физической величины, меняющим состояние частицы. Поэтому в результате измерения должна измениться волновая функция данного состояния. Таким образом, процесс измерения следует описывать правилом, по которому меняется волновая функция, т.е. следует задать соответствующую «функцию от

функции» или оператор физической величины ˆ , сопоставляющий волновой функции одного

A

состояния волновую функцию другого состояния . Математически процесс измерения

Допустим, что при измерении некоторой физической величины в состоянии с волновой функцией 1 получается одно значение А1, а в состоянии с 2 – другое: А2. Какое значение получится при измерении физической величины в состоянии, являющимся суперпозицией этих

состояний: 3=с1 1+с2 2?

Процесс измерения любой физической величины носит вероятностный характер. Т.е. тот или иной результат измерения можно получить с какой-то определённой вероятностью. Это означает, что при однократных измерениях мы будем получать значения А1 или А2 с некоторыми, вообще говоря, разными вероятностями р1 и р2 .

Замечание. Состояние, в котором при однократных измерениях физических величин всегда получаются одни и те же значения, принято называть чистым состоянием. В обратном случае, состояние называют смешанным.

Требования, чтобы измерения сводились к операциям над волновыми функциями, приводят к условию, налагаемому на математическое выражение для волновой функции: она должна быть функцией, принимающей значения в комплексном пространстве. Поэтому для неё справедливы все операции над комплексными числами.

Математическое отступление.

Напомним, что символом i обозначается такое комплексное число, что i2 1 .

Любое комплексное число z может представлено в виде z x i y , где x и y – вещественные числа. При этом число x называется вещественной частью числа z и обозначается x Re z , а

надо знаменатель и числитель дроби умножить на комплексно сопряжённое число к знаменателю:

6

f ei , поэтому ei cos i sin . Это соотношение позволяет привести ещё более корот-

Замечание. ei cos2 sin2 1 .

Уравнение Шрёдингера.

Волновая функция должна являться решением уравнения Шрёдингера:

где m – масса частицы, i2 1, U – действительная функция координат и времени, такая, что вектор gradU является классическим аналогом силы, действующей на частицу. В случае, когда U не зависит от времени, она совпадает с потенциальной энергией.

Следовательно, волновая функция должна быть непрерывно-дифференцируемой один раз по

времени и два раза по пространственным координатам.

гера (по имени немецкого физика Эрвина Шрёдингера, предложившего его в 1926 году). Уравнение Шрёдингера является одним из постулатов (аксиом) квантовой механики и

играет в квантовой физике такую же фундаментальную роль, как уравнения Ньютона в классической механике и уравнения Максвелла в классической электродинамике.

Уравнение Шрёдингера является линейным, т.е. линейная комбинация решений тоже является решением. Действительно, если каждая из функций 1 и 2 является решением, то их линейная комбинация 3=с1 1+с2 2 (где с1 и с2 – некоторые константы) тоже является реше-

7

Семестр 4. Лекции 3-4.

Следовательно, принцип суперпозиции состояний не противоречит уравнению Шрёдингера.

Замечание. Сопряжённое уравнение Шрёдингера для волновой функции имеет вид:

Пример. Найдем волновую функцию для свободно движущейся частицы в одномерной области (волны де Бройля). В этом случае U = 0, поэтому уравнение Шрёдингера принимает вид:

Решение этого уравнения ищем в виде плоской волны (С=const):

C ei kx t C cos kx t i sin kx t .

После подстановки в уравнение выражений для производных

ской энергии в классической физике E EK U .

Замечание. Для свободной частицы квадрат модуля волновой функции равен:

2 Cei kx t 2 C 2 cos2 kx t sin2 kx t C 2 .

8

Семестр 4. Лекции 3-4.

b

Поэтому интеграл P a x b 2 dx C 2 b a имеет смысл только для ограниченной

a

области.

Условие нормировки.

Уравнение Шрёдингера линейное, поэтому если решением является функция , то решением является также и функция 1 с , где n =const. В этом смысле говорят, что волно-

вая функция определяется с точностью до константы.

Из физического смысла следует, что для всей области определения волновой функции V справедливо утверждение – вероятность того, что частица находится в этой области V, равна единице:

P V 2dV 1.

V

Следовательно, если при решении задачи о поиске волновой функции в некоторой области бы-

Правило выбора решения , такого, что для него во всей области выполняется условие

P V 2dV 1

V

называется условием нормировки решения на единицу или просто условием нормировки.

Замечание. В принципе, формально можно выбрать и другое условие нормировки – например:2dV 2 ,

V

но тогда квадрат модуля волновой функции уже не будет иметь смысл плотности вероятности.

Вектор плотности потока вероятности.

В классической физике из уравнений движения частиц или уравнений Максвелла следуют разнообразные законы сохранения и уравнения непрерывности. Посмотрим, как обстоит дело с уравнением Шрёдингера.

Если частица не находится постоянно в некоторой области пространства V, то вероятность её нахождения в этой области должна зависеть от времени. Поэтому в этом случае

Из сопряжённого уравнения Шрёдингера:

9

С учётом теоремы Остроградского-Гаусса получаем:

где в правой части стоит поток вероятности через поверхность S , который и приводит к изменению вероятности P . Введём вектор плотности потока вероятности j следующим соотношением:

j 2im grad * * grad .

Тогда для скорости изменения вероятности получим интегральное соотношение:

dP j ,dS , dt S

которое является уравнением непрерывности для поля вероятности в интегральной форме. Его физический смысл заключается в следующем: изменение вероятности нахождения частицы в

Стационарные состояния.

Особенности движения микрочастиц в тех или иных силовых полях можно выявить, рас-

сматривая стационарные состояния – состояния, в которых полная энергия частицы остаётся постоянной. В этом случае плотность вероятности пребывания частицы в ка- кой-либо точке пространства не зависит от времени. Волновая функция, описывающая стационарное состояние частицы, является решением уравнения Шрёдингера для стационарных состояний.

10