Физика_Л_11

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный технический университет им. H.Э.Баумана

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

личина объёма общей области в фазовом пространстве равна: V V

p3 . Тогда общее ко-

p3 . Тогда общее ко-

личество узлов равно:

личество узлов равно:

.pdf

Скачиваний:

Добавлен:

23.03.2016

Размер:

591.54 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

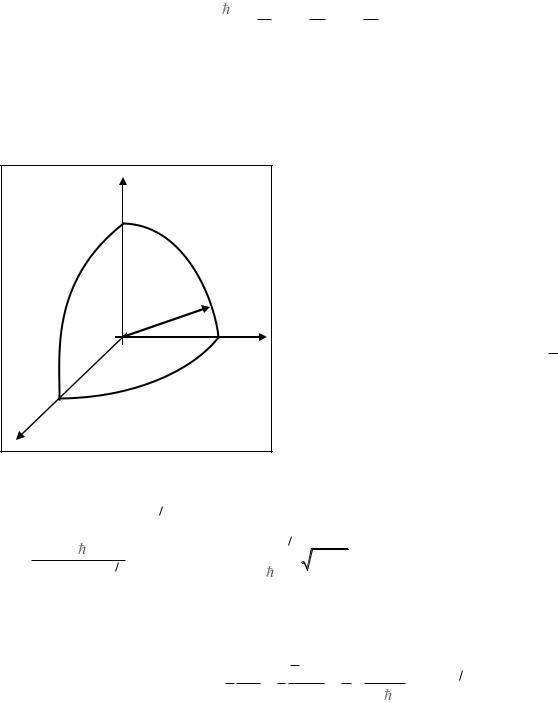
Семестр 4. Лекции 11.

Лекции 11. Квантовые статистические распределения.

Плотность квантовых состояний. Распределение Ферми - Дирака. Функция

распределения частиц по энергиям. Энергия Ферми. Вырожденный электрон-

ный газ, температура вырождения. Распределение Бозе - Эйнштейна. Фото-

ны и фононы. Вывод формулы Планка из квантовой статистики Бозе - Эйн-

штейна.

Плотность квантовых состояний.

Энергия электрона, находящегося в трёхмерной потенциальной яме с непроницаемыми

стенками, описывается выражением:

n2 2

E 2m

где

a1 , a2 ,

a3 – длины сторон прямоугольной ямы. Энергия электрона меняется не непрерывно,

а дискретно, т.к. числа n1, n2, n3

могут принимать только целочисленные значения. Однако, ес-

ли энергия частицы существенно больше энергии основного состояния, то разница между зна-

чениями энергии

соседних

уровней

Е значительно меньше самого значения энергии:

E E , тогда можно считать, что энергия электрона меняется практически непрерывно (ква-

зинепрерывно).

Введём трёхмерное пространство, вдоль трёх

взаимно перпендикулярных осей которого отложены

квантовые числа n1, n2, n3 (пространство кванто-

вых чисел). Точка этого пространства, координата ко-

торой задаётся набором целым чисел (n1, n2, n3), назы-

вается узлом. Каждому узлу в пространстве квантовых

чисел соответствует определённое значение энергии.

Одному значению энергии электрона может соответ-

ствовать несколько состояний (например, отличаю-

щихся проекциями спина электрона

1 ). Узлу можно

сопоставить элементарный кубик с единичной дли-

ной рёбер: n1

n2 n3 1, так что объём этого ку-

бика равен единице: V n1 n2

n3 1 .

Пусть N – количество узлов, в которых энергия

электрона

не превышает некоторое

фиксированное

значение

Если

ввести обозначение

n a a

2 a n a

2 a a n

то

выражение

для

энергии

примет

вид:

1 2 3

2 3

a a a

4 3

r2 ,

откуда

a a a

1 3

2m E

. Тогда число узлов N

равно отношению

2me a1a2a3 2 3

объёмов этой восьмой части сферы соответствующего радиуса (в которой все три координаты

неотрицательные {n1>0, n2>0, n3>0} (т.е. в одной восьмой части сферы)) к объёму элементарно-

го кубика:

1 Vсф

a a a

2m E

3 2

8 V

1 2 3

8 V 6

3 3

Семестр 4. Лекции 11.

Ниже учтём, что объём потенциальной ямы (в обычном пространстве) равен: V a1a2a3 , а величина p 2me E - величина (нерелятивистского) импульса. Поэтому

Vp3

2 3

3 3

6 23 3 3

Теперь рассмотрим фазовое пространство, каждая точка в котором задаётся 6-ю

координатами – это три пространственные

координаты и три проекции

импульса

x, y, z, px , py , pz . Частица, находящаяся в потенциальной яме,

в состояниях, энергия которых

не превышает некоторое значение E, движется в некоторой области шестимерного фазового

пространства.

Т.к. величина импульса частицы не превосходит величины p 2me E , то в импульсной

части фазового пространства p

, p

эта область задается соотношением p2

p2 p2 -

т.е. является шаром радиуса p,

объём которого V

p3 . Поэтому полная область в 6-ти

мерном фазовом пространстве является прямым произведением прямоугольной трёхмерной ямы в обычном пространстве и шара в импульсном пространстве. Следовательно, ве-

Обозначим возможное количество состояний, приходящихся на один узел как qs . Например, для электрона qs 2 , т.к. возможны два состояния с одинаковым набором квантовых чисел, но различающиеся проекциями спина. Тогда общее число состояний G со значением

энергии не больше E, равно:	G N qs	Vфаз		qs .
		2	3
Замечание. Минимальное количество квантовых состояний (при qs 1) равно:					G0	Vфаз		.
						2	3

Тогда элементарный объём фазового пространства, приходящийся на одно квантовое состояние, можно определить как отношение фазового объёма к количеству состояний:

V	Vфаз	2 3 . Учитывая соотношения неопределённостей Гейзенберга для координат и

фаз	G0

проекций импульсов, записанные в виде x px 2			, y py 2 , z pz 2 , получаем

выражение для элементарного объёма фазового пространства, соответствующего одному квантовому состоянию: 2 3 x y z px py pz Vфаз .

В общем случае для количества состояний справедливо соотношение: G Vфаз qs .

Vфаз

Плотностью квантовых состояний называется такая функция g E , зависящая от

энергии, что количество квантовых состояний, энергия которых не превышает значения

dG E

E0, определяется равенством:

G E0 0

g E dE ,

т.е.

g E

Т.к. можно записать: g E

dG E dp

, то в рассматриваемом случае получаем равенство:

dp dE

Семестр 4. Лекции 11.

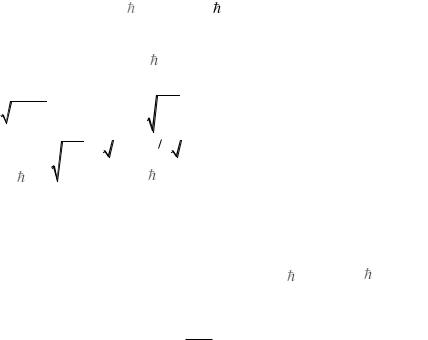
g E

dp d

Vp3

V 4 p2

2 3

dE dE dp

Оказывается, что полученное выражение g E q

V 4 p2

справедливо для любых частиц.

s 2

Пример.

2 и

1) Для электронов: q

2m E

тогда

поэтому

3 2

g E 2

V 4 2m E m

V .

2 3

2) Для фотонов можно считать, что qs 2 , что соответствует двум независимым направлениям

								E 2
							V 4
							V 4
поляризации э/м волны. Т.к. p	E	, то	dp	1	. Поэтому	g E 2	c
	c						2	3

			dE	c

1	E2	V .
c	2 3c3

В классической физике распределение частиц по энергиям в фазовом пространстве опи-

EK U

сывается распределением Максвелла-Больцмана: dN A e kT dpx dpy dpz dxdydz , где ЕК и U -

кинетическая и потенциальная энергии частицы, Т - температура, k - постоянная Больцмана, A - нормировочный коэффициент.

Для вывода статистических распределений необходимо найти наиболее вероятное распределение частиц, т.е. распределение, которое может быть реализовано наибольшим числом способов. По основному постулату статистической физики именно это распределение и является равновесным.

Предположим, что частицы не взаимодействуют друг с другом (модель идеального газа), а также, что все распределения, которые приводят к одной и той же суммарной энергии частиц, реализуются с одинаковой вероятностью.

Рассмотрим систему, состоящую из двух частиц. Пусть число возможных состояний, в которых может находиться каждая из частиц, равно трём.

По классическим представлениям две частицы всегда различимы. Присвоим частицам номера 1 и 2. Если в каком-то состоянии частицы переставить просто местами, то получится новое состояние. Поэтому общее число состояний системы равно 9.

В квантовой механике тождественные частицы принципиально неразличимы. При перестановке местами тождественных частиц состояние системы не меняется. Поэтому занумеровать частицы нельзя. Если в одном состоянии может находиться только один фермион, то для бозонов никаких ограничений нет. Поэтому число состояний системы из бозонов равно 6, а из фермионов равно 3.


	1	2		2	1		12


Распределение классических частиц		1	2		2	1		12


	1		2	2		1			12




Распределение			Распределение


бозонов			фермионов

Семестр 4. Лекции 11.

Распределение Бозе-Эйнштейна.

Рассмотрим следующую вспомогательную задачу. Пусть имеется длинный пенал, который может быть разделён на Z ячеек с помощью (Z-1) перегородок. Найдем число способов размещения N неразличимых частиц по ячейкам. В каждой ячейке может находиться произвольное число бозе-частиц. Будем считать, что система состоит из N частиц и (Z-1) перегородок, т.е. всего из N+Z-1 элементов. Общее число перестановок в системе из N+Z-1 элементовравно (N+Z-1)! . Однако перестановки частиц (из-за их неразличимости) ничего не меняют. Число таких перестановок равно N! . Перестановки только перегородок тоже не приводят к новым распределениям, их число равно (Z-1)! . Таким образом, число способов , с помощью которых N тождественных частиц могут быть распределены по Z ячейкам, равно:

N Z 1 !

N! Z 1 ! .

Это выражение определяет число способов, с помощью которых N бозонов могут быть распределены по Z состояниям. Каждый способ размещения частиц представляет собой опре-

делённое микросостояние системы. Следовательно, - это число микросостояний, с помощью которых реализуется конкретное макросостояние системы. Т.е. - это термодинамическая вероятность или статистический вес макросостояния системы.

В шестимерном фазовом пространстве уравнение f x, y,z, px , py , pz E const , где E -

энергия частицы, определяет изоэнергетическую поверхность, т.е. поверхность, все точки

которой отвечают одному и тому же значению энергии частицы.


Слой с номером i между двумя поверхностями
	f	x, y,z, px , py , pz Ei и		f x, y,z, px , py , pz Ei 1
		Ei	Ei . В этом случае энергию всех частиц, попадающих в i-й
будет тонким, если	Ei 1	Ei	Ei . В этом случае энергию всех частиц, попадающих в i-й

слой, можно считать одинаковой и равной Ei . Пусть число квантовых состояний для этого

слоя равно Zi , а количество частиц в пределах i- го

слоя равно Ni . Тогда статистический вес

подсистемы, содержащей

Ni частиц, равен:

Zi 1 !

Ni! Zi

1 !

Статистический вес всей системы равен произведению статистических весов отдельных

её подсистем: i i

Ni Zi

1 !

N ! Z

1 !

Надо найти распределение, которое может быть реализовано наибольшим числом спосо-

бов, т.е. распределение, для которого статистический вес

максимален. Т.е. нужно найти

максимум выражения

Ni Zi 1 !

при заданном числе частиц системы

N ! Z

1 !

N Ni и полной энергии системы

E Ni Ei .

1 !

Вместо поиска экстремума выражения

будем искать мак-

N ! Z

1 !

симум энтропии

S, которая

связана

со

статистическим

весом

соотношением

Больцмана

S k ln :

S k ln

Zi 1 !

ln N

1 ! ln N !

ln Z

Ni! Zi 1 !

Для дальнейших преобразований воспользуемся формулой Стирлинга, согласно кото-

рой при n 1 :

ln n! nln n n .

При

Zi 1

получаем:

Семестр 4. Лекции 11.

S k

1 ln N

1 N

ln N

1 ln Z

или S k

1 ln N

1 N

ln N C ,

где величина

C k

1 ln Z

- не зависит от числа частиц Ni .

Чтобы найти максимум энтропии для заданного числа частиц системы

N и энергии E,

применяем метод множителей Лагранжа, согласно которому необходимо построить вспомога-

тельную функцию

F S 1N 2 E (где

1 и 2

– постоянные множители) и найти её экс-

тремум:

F k

1 ln N

1 N

ln N

N E .

i i

Необходимые условия экстремума

имеют вид:

ln Ni

1 Ni Zi 1

ln Ni

2 Ei 0

Ni Zi

или

Ni Zi 1

1 2 Ei

откуда

k .

Отношение

представляет собой среднее число частиц, приходящихся на одну

ячейку фазового пространства, т.е. на одно состояние в i-ом энергетическом слое.

Поскольку Z

1, то слагаемым в числителе

1 можно пренебречь. Тогда

для

получаем:

1 2 Ei

Найдем множители Лагранжа 1

Т.к. все частные производные функции F равны нулю,

то это

означает,

что

равен

нулю

дифференциал

этой

функции

dF,

т.е.

dF dS 1dN 2dE 0 . Но так как число частиц системы

N постоянно, то dN = 0 и, поэто-

му dS 2dE .

Предположим теперь, что рассматриваемая система получает в обратимом процессе некоторое количество теплоты Q при неизменном объёме V. Поэтому изменение энтропии си-

стемы равно dS

Q . Поскольку

V=const,

то A=0

и Q dE , следовательно,

откуда

Множитель 1

запишем в

виде:

, где - некоторая функция пара-

метров состояния системы, в частности,

температуры. Эту функцию называют химическим

потенциалом. С учетом выражений для

выражение для ni принимает вид:

. Освобождаясь от индекса i,

окончательно получаем распределение Бозе-

e kT

Эйнштейна:

e kT

Семестр 4. Лекции 11.

Оно описывает распределение бозе-частиц по энергиям и определяет среднее число бозечастиц n , находящихся в квантовом состоянии с энергией E. Величину n называют

также числом заполнения энергетического уровня с энергией E.

Как следует из распределения Бозе-Эйнштейна, число бозе-частиц, находящихся на одном энергетическом уровне (в одном состоянии), ничем не ограничено и при малых значениях

параметра	E	может оказаться очень большим. Это важная отличительная особенность бо-
	kT

зе-частиц.

Замечание. Химический потенциал для систем бозонов с постоянным числом частиц N может принимать только отрицательные значения, т.е. < 0. Действительно, если бы мог быть положительным, то при E < экспонента в знаменателе была бы меньше единицы:

e kT

1 и соответствующие числа заполнения

стали бы отрицательными, что невозмож-

но.

Рассмотрим случай малых чисел заполнения:

n 1. Это условие выполняется при

e kT

или

1 .

Пренебрегая единицей по сравнению с экспонентой в знаменателе,

получаем:

A e

kT , где

A ekT .

Мы видим, что при малых числах заполнения,

e kT

или, как говорят, в случае разреженного бозе-газа,

распределение Бозе-Эйнштейна перехо-

дит в классическое распределение Больцмана.

Газ,

свойства которого отличаются от свойств классического идеального газа,

называется вырожденным газом. Поскольку распределение Бозе-Эйнштейна существенным образом отличается от распределения Больцмана, то газ бозонов является вырожденным га-

зом. И только в случае малой плотности ( n 1) вырождение снимается и разреженный бозе-

газ ведет себя подобно идеальному газу.

Число бозонов, находящихся на одном энергетическом уровне, может быть очень большим. Кроме того, при определённых условиях в системе бозе-частиц может происходить бозе-

конденсация - скопление очень большого числа частиц в состоянии с энергией E=0. Имен-

но с бозе-конденсацией связаны такие явления, как сверхтекучесть и сверхпроводимость. Распределение Бозе-Эйнштейна используется для описания свойств систем, состоящих

из бозе-частиц: как простых, например, фотонов, фононов, так и более сложных, составных, например, атомов 4 He , электронов, образующих куперовские пары, и т.д. С его помощью описываются свойства теплового излучения, теплоёмкость кристаллов и многие другие физические явления. Что же касается поведения обычных газов, атомы которых являются бозе-частицами, то анализ показывает, что при нормальных температурах и давлениях эти газы не являются вырожденными и подчиняются классической статистике. Вырождение наступает либо при очень низких температурах, либо при очень высоких давлениях, т.е. при тех условиях, при которых газы перестают быть идеальными. Таким образом, для этих газов статистика Бозе-Эйнштейна в той области, в которой справедлива кинетическая теория газов, практически не отличается от классической статистики Больцмана.

Случай переменного числа частиц.

При выводе распределения Бозе-Эйнштейна число частиц системы N оставалось постоянным. Какой вид имеет распределение Бозе-Эйнштейна для системы с переменным числом частиц? Примером такой системы является тепловое излучение внутри замкнутой полости. Стенки полости непрерывно поглощают и испускают излучение, поэтому число фотонов внутри полости постоянно меняется. Фотоны являются бозе-частицами и при не очень сильных (нелазерных) интенсивностях излучения не взаимодействуют друг с другом. Так что излучение в за-

Семестр 4. Лекции 11.

мкнутой полости представляет собой идеальный бозе-газ фотонов с переменным числом частиц.

Рассмотрим систему бозонов с переменным числом частиц N. Решаем задачу также как и выше. Поскольку в данном случае Ni N const , то при нахождении условного экстре-

мума энтропии S методом множителей Лагранжа вместо функции F S 1N 2 E следует взять функцию F S 2 E (исчезло условие постоянства числа частиц системы). Поэтому со-

ответствующий множитель Лагранжа 1 = 0 . В силу того, что химический потенциал и множитель 1 связаны соотношением = 1Т, получаем, что и =0. Таким образом, химиче-

ский потенциал системы бозонов с переменным числом частиц равен нулю и распределе-

ние Бозе-Эйнштейна для систем с переменным числом частиц принимает вид:

n	1		.

		E

	ekT 1

Пример. Получим формулу Планка для равновесного теплового излучения из распределения Бозе-Эйнштейна.

Рассмотрим излучение, находящееся внутри замкнутой полости, стенки которой нагреты до некоторой температуры Т. Это излучение представляет собой идеальный газ фотонов. По-

скольку для фотонов E	, то	n	1		.



				1
			ekT	1

Энергия излучения в узком энергетическом интервале от E до E+dE складывается из энергий отдельных фотонов. Плотность квантовых состояний g(E), т.е. число состояний, приходящихся на единичный энергетический интервал, для фотонов определяется выражением:

g E

V .

Произведение g(E) на

dE дает число квантовых состояний, заключённых

3c3

внутри интервала

dE. Умножая это произведение на среднее число фотонов в данном состоя-

нии

и на энергию фотона E, получаем, что суммарная энергия фотонов в интервале dE

равна:

n g E EdE .

Данному энергетическому интервалу (от E до E+dE) соответствует частотный интер-

вал, т.е. интервал

частот от

до

. Получим выражение для той же са-

мой энергии с помощью объёмной спектральной плотности энергии излучения u ,T , которая представляет собой энергию излучения в единичном частотном интервале, отнесённую к еди-

нице объёма. Т.к. энергия фотонов в частотном интервале d

равна

u ,T V d , (V - объём

полости), то

V d

n g E EdE

или

V EdE

2 3c3

ekT 1

откуда приходим к формуле Планка:

u ,T

2c3

ekT

Следует отметить, что именно с этой формулы началось становление квантовой механики.

Распределение Ферми-Дирака

Найдем распределение ферми-частиц, т.е. частиц, обладающих полуцелым спином. Фер- ми-частицы подчиняются принципу (запрета) Паули, согласно которому в одном и том же состоянии одновременно не может находиться более одного фермиона. Т.е. можно сказать, что

Семестр 4. Лекции 11.

фермионы являются частицами-индивидуалистами. Рассмотрим идеальный ферми-газ, т.е. систему, состоящую из невзаимодействующих фермионов.

Сначала найдем число возможных распределений N частиц по Z ячейкам пенала при условии, что в каждой ячейке не может находится более одной частицы. Число ячеек Z и число частиц N должны удовлетворять условию Z N.

Число всевозможных перестановок пустых ячеек пенала и ячеек с частицами равно Z! . При этом перестановки только ячеек с частицами в силу тождественности частиц не приводят к новым распределениям. Число таких перестановок равно N! . Перестановки местами пустых ячеек тоже не дают новых распределений, их число равно (Z N)! . Таким образом, число различных распределений N частиц по Z ячейкам в данном случае равно:

N! Z N !

Это выражение определяет число возможных распределений

фермионов по Z

ячейкам, т.е. статистический вес макросостояния системы фермионов.

Вывод статистического распределения, которому подчиняются ферми-частицы, прово-

дится также как и для бозе-частиц.

В шестимерном фазовом пространстве с координатами x, y, z, px , py , pz

две изоэнерге-

тические поверхности f x, y,z, p

, p

E const и

f x, y , z , p

, p

const вы-

i 1

деляют тонкие энергетические слои. Опять предполагаем, что

Ei 1

Ei .

Пусть в i-ом

слое имеется Zi

ячеек и Ni

частиц. Тогда статистический вес подсистемы из Ni

частиц есть

Zi!

. Статистический вес всей системы равен произведению статистических весов

Ni! Zi Ni !

её отдельных подсистем:

Zi!

N ! Z

Для того чтобы найти наиболее вероятное распределение частиц по ячейкам, нужно

найти максимум статистического веса

при условии,

что полное число частиц системы

N и

полная энергия

системы

остаются

постоянными,

т.е.

N Ni

const

E Ni Ei const .

Как и для бозе-частиц, вместо максимума статистического веса будем искать максимум энтропии S k ln :

S k ln		Zi!	k	ln Z ! ln N ! ln Z				N	! .
S k ln			k	ln Z ! ln N ! ln Z				N	! .
		Ni! Zi Ni !			i	i	i	i
	i	Ni! Zi Ni !		i

Используем формулу Стирлинга: ln n! nln n n , которая справедлива при n 1. Поэтому

при Zi 1

Ni 1 , выполняется:

S k

ln Z

ln N

ln Z

или

S k

ln Z

ln N

ln Z

S С k

ln N

где

С k

ln Z

Слагаемое

можно в дальнейшем не учитывать, поскольку при решении задачи на экстре-

мум энтропии S варьироваться будут только числа частиц в слое

, а

от них не зависит.

Семестр 4. Лекции 11.

Для отыскания максимума энтропии используем метод множителей Лагранжа. Рассмотрим функцию F S 1N 2 E , где

F С k

ln N

N E

i i

1 и 2 - множители Лагранжа. Равенство нулю частных производных этой функции по Ni :

1 ln Z

1 2 Ei

k ln N

E 0 ,

откуда

k .

Отношение

представляет собой среднее число ферми-частиц, приходящихся

на одну ячейку, т.е. на одно квантовое состояние:

1 2 Ei

Множители

Лагранжа 1

находятся точно

также

как

в случае бозе-частиц:

где - химический потенциал.

Тогда

e kT 1

Освобождаясь от индекса

i, приходим к окончательному выражению для среднего

числа фер-

ми-частиц, приходящихся на одно квантовое состояние:

e kT

Это соотношение называется распределением Ферми-Дирака. Оно определяет среднее число ферми-частиц, находящихся в квантовом состоянии с энергией E.

Следствия из распределения Ферми-Дирака.

1. n не может быть больше единицы. Это означает, что в одном квантовом состоянии не может находиться более одной ферми-частицы, что согласуется с принципом Паули. По-

скольку n 1, то говорят, что распределение Ферми-Дирака определяет вероятность заполнения энергетического уровня с энергией E при температуре T.

2.Химический потенциал для ферми-частиц может быть только положительным, т.е.

> 0. Иначе при T 0 экспонента в знаменателе обратилась бы в бесконечность, а числа заполнения - в нуль, чего быть не может.

Рассмотрим случай малых чисел заполнения:

1. Это условие выполняет-

e kT 1

n e

A e

ся при e kT 1, но тогда

где

A ekT , т.е. распределение Ферми-

Дирака при малых числах заполнения (говорят, в случае разреженного ферми-газа) переходит в классическое распределение Больцмана. Т.к. в распределение Больцмана в случае ма-

лых чисел заполнения переходит также и распределение Бозе-Эйнштейна, то можно сделать вывод, что разреженные квантовые газы (и в случае бозонов, и в случае фермионов) не явля-

ются вырожденными и подчиняются классической статистике.

Принципиальное различие между распределениями Ферми-Дирака и Больцмана наблю-

дается при	E	1 . Классические частицы могут накапливаться в одном и том же состоянии
	kT

в большом количестве. Для них n тем больше, чем меньше энергия состояния E. Что же ка-

сается ферми-частиц, то максимальное их число в одном квантовом состоянии не может превышать единицу, что согласуется с принципом запрета Паули.

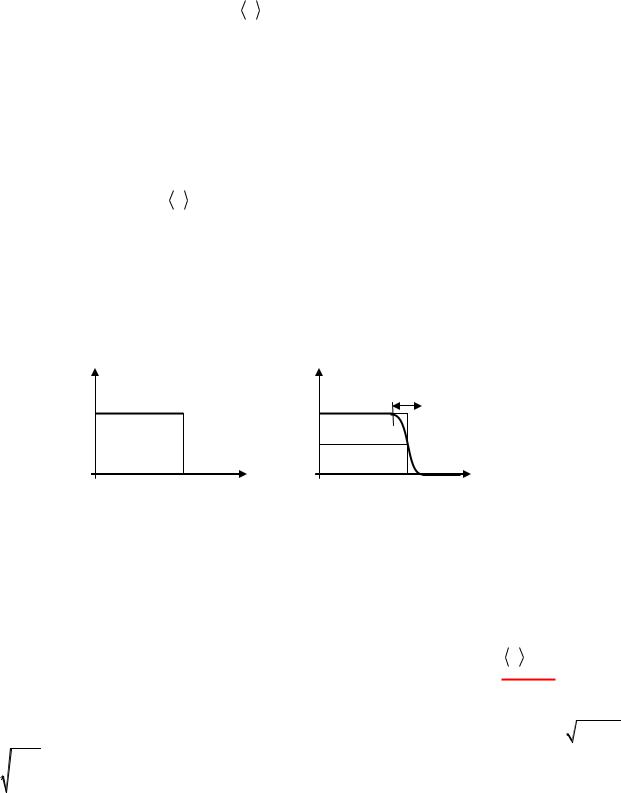
Семестр 4. Лекции 11.

Химический потенциал , который имеет размерность энергии, в случае ферми-частиц называют энергией Ферми или уровнем Ферми и обозначают EF. При этом распределение Ферми-Дирака принимает вид:

n	1			.

		E EF

	e kT		1

Т.к. для фермионов > 0, то энергия Ферми EF > 0 также больше нуля. (Энергия Ферми EF медленно меняется с изменением температуры T).

Рассмотрим зависимость распределения Ферми-Дирака от температуры. Будем считать, что рассматриваемая температура T может быть сколь угодно близка к абсолютному нулю, т.е. T 0. Обозначим через EF(0) значение энергии Ферми при T 0. Этот случай будем условно называть случаем «нулевой температуры: T = 0». Из распределения Ферми-Дирака следует, что в случае T = 0:

1,	E E	F		0
		F		0 .
n 0,	E E		F	0 .
			F

Это означает, что все квантовые состояния с энергиями E EF 0 оказываются занятыми фермионами, а все состояния с энергиями E EF 0 - свободными. Таким образом, при T = 0

энергия Ферми EF(0) является максимальной энергией, которой могут обладать фермичастицы.

Распределение Ферми-Дирака в этом случае представляет собой ступенчатую функцию

< n >	T=0		< n >	T >0	kT
	T=0			T >0

1			1
1			1
			1/2
		E				E
			0
0	EF(0)		0		EF(0)

единичной высоты, обрывающуюся при E EF 0 . При отличных от нуля температурах рез-

кий скачок < n > от единицы до нуля становится более размытым и происходит в области энергий, шириной порядка нескольких kT. Чем выше температура, тем шире область, в которой < n > меняется от единицы до нуля, и тем более плавно происходит переход от заполненных со-

стояний к незаполненным. Однако, при любой температуре при E=EF	n	1	. Т.е. в со-
		2

стоянии с энергией, равной энергии Ферми, всегда находится один электрон.

Наряду с энергией Ферми EF при анализе поведения ферми-частиц вводятся также им-


пульс		Ферми pF и		скорость Ферми vF, определяемые соотношениями: pF 2me EF ,

v		2EF	. При T = 0	это максимальные импульс и скорость, которыми могут обладать
v	F		. При T = 0
	F	me
		me

ферми-частица.

Электронный газ в металлах

Применим статистику Ферми-Дирака к описанию электронов проводимости в металлах. Будем рассматривать свободные электроны, т.е. ту часть атомных электронов, которая может

1 / 21 2 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
16.04.201969.72 Кб3физика шпоры (Автосохраненный).docx
#
25.04.2019362.63 Кб12физика шпоры (Автосохраненный).docx
#
24.12.201812.47 Mб72Физика-Дополненная.doc
#
12.08.2019493.48 Кб7Физика. ответы на экзамен.docx
#
12.03.2015545.31 Кб51Физика_Л_1-2.pdf
#
23.03.2016591.54 Кб15Физика_Л_11.pdf
#
23.03.2016450.37 Кб16Физика_Л_12.pdf
#
23.03.2016462.17 Кб17Физика_Л_15.pdf
#
12.03.2015559.35 Кб38Физика_Л_3-4.pdf
#
12.03.2015537.92 Кб32Физика_Л_5-6.pdf
#
09.02.201559.44 Кб8физра.docx