книги / Сопротивление грунтов (некоторые лекции по курсу Механика грунтов )

как вблизи σI, так и вблизи σIII. Для количественной характеристики положения σII вводится параметр, предложенный Лоде и Надаи:

Если σII = σI, μσ = +1, а если σII = σIII, μσ = –1. Очевидно, что значению μσ = 0 соответствует положение σII в центре главного круга Мора.

В теории упругости касательные напряжения часто выражают через второй инвариант напряжений. Различают октаэдрическое (т.е. отнесенное к равно наклоненной к осям σI, σII и σIII площадкам):

2 Что такое деформация

Справки из интернета: «Деформация – лат. Deformatio, искажение: 1. Изменение взаимного расположения точек твердого тела, при котором меняется расстояние между ними, в результате внешних воздействий. Д. называется упругой, если она исчезает после удаления воздействия, и пластической, если она полностью не исчезает. Наиболее простые виды Д. – растяжение, сжатие, изгиб, кручение». И еще: «2. В переносном смысле Д. – изменение формы, искажение сущности чего-либо (напр., деформация социальной структуры)».

Деформации обозначают латинской е (от лат. elasticitat – упру-

Так же, как и напряжения, деформации обозначают в виде матрицы, в которой помещают элементы матрицы: по главной диагонали – нормальные деформации (в направлениях, перпендикулярных площадкам), а в строках – касательные деформации (в направлениях, параллельных площадкам). В целом матрица характеризует тензор деформаций Тε, а ее элементы – компоненты тензора деформаций:

61

Подобно напряжениям, парные индексы нормальных деформаций

заменяют на одиночные – εхх на εх, εzz – на εz и др., а компактную форму записи тензора деформаций представляют как Тε = {εij} (i, j = 1, 2, 3).

В качестве первого направления обычно принимают ось Z, а в качестве второго – ось Y, третьего – Х (но иногда и по-другому).

Тензор деформаций для главного направления будет выглядеть так:

Обозначение инвариантов тензора деформаций подобно соответствующим инвариантам тензора напряжений:

– первый (линейный) инвариант Iε = εхх + εyу + εzz = εI + εII + εIII = = const; причем: εI > εII > εIII; первый инвариант будет характеризовать

объемное сжатие грунта;

– второй (квадратный) инвариант IIε = (εI – εII)2 + (εI – εIII)2 +

+(εIII – εI)2 = const; этот инвариант характеризует объемный сдвиг грунта;

–третий (кубический) инвариант IIIε = εI ·εII · εIII = const.

Как видно, здесь сохранено прежнее обозначение инвариантов, но

с соответствующим индексом – ε вместо σ (в некоторых источниках их называют по-другому – J1, J2, J3 или I1ε, I2ε, I3ε и др.).

Для последующего анализа полезно отметить следующие характеристики деформаций:

– средняя объемная деформация

– деформации по равно наклонным площадкам (октаэдрический сдвиг)

– или обобщенная деформация (либо интенсивность деформаций сдвига)

62

3 Как напряжения связаны с деформациями

Упругость – фундаментальное свойство тел деформироваться под действием нагрузки и восстанавливать первоначальную форму и размеры после ее снятия. Понятие «упругость» поясняется с использованием примеров из интернета, популярных учебников (Н.И. Безухов, 1981 [1]; М.Н. Гольдштейн, 1971 [2]; см. также интересную брошюру Д. Гордона, 1971 [3]).

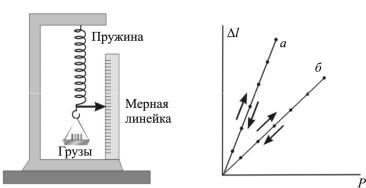
Проявление упругости лучше всего проследить, проведя простой опыт с пружинными весами – динамометром (рис. 2.5).

При нагрузке в 1 кгс стрелка-индикатор сместится на 1 деление, при 2 кгс – на два деления и т.д. Если нагрузки последовательно снимать, процесс идет в обратную сторону. Пружина динамометра – упругое тело, а ее удлинение l, во-первых, пропорционально нагрузке P, во-вторых, полностью исчезает при полном снятии нагрузки.

Если построить график, отложив по горизонтальной оси величины нагрузки, а по вертикальной – удлинение пружины, то получаются точки, лежащие на прямой, проходящей через начало координат (рис. 2.6). Это справедливо как для точек, изображающих процесс нагружения, так и для точек, соответствующих нагрузке, причем прямая а соответствует более мягкой, а прямая б – более жесткой пружине.

Тангенс угла наклона характеристики называется жесткостью пружины С. Теперь можно записать уравнение деформирования пружины l = P / C.

Жесткость пружины С имеет размерность кгс/см (тс/м, кН/м и т.п.) и зависит от материала пружины (например, сталь или бронза) и ее размеров – длины пружины, диаметра ее витка и толщины проволоки, из которой она сделана.

Проявление упругих свойств было давно известно и широко использовалось людьми. Выше уже говорилось о том, что современное понима-

63

ние упругости впервые появилось у Роберта Гука (R. Hooke, 1635–1722), современника (и соперника) И. Ньютона (I. Newton, 1643–1727). В 1660 г. Р. Гук сформулировал свое открытие очень кратко в виде афоризма: «Ut tensio sic vis» («Какова сила, таково и удлинение») и записал его в виде F = –k x, где F – сила, x – линейное растяжение или сжатие образца,

аk – коэффициент упругости.

В1807 г. Т. Юнг (Т. Young, 1773–1829) ввел термин «модуль упру-

гости», впоследствии получивший название модуля Юнга и обозначение Е (от лат. Elasticitat). Вместо силы F (как первоначально у Гука) Юнг предложил учитывать напряжения σ, а вместо удлинения-укоро- чения х – относительные деформации ε. В отличие от коэффициента упругости Гука k модуль упругости Е представляет собой фундаментальную характеристику (константу) для любого материала.

Тем не менее основной закон теории упругости о пропорциональной связи между напряжениями и деформациями вошел в историю как закон Гука, но, что вполне заслуженно, с «именным» коэффициентом пропорциональности – модулем упругости Юнга:

Физическая природа упругости обусловлена электромагнитным взаимодействием (в том числе в решетках кристаллов). В частности, доказано, что упругие деформации вещества связаны с изменением рас-

стояния между его атомами.

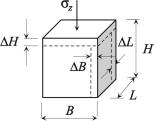
Упругое тело имеет еще одно фундаментальное свойство – сужаться при растяжении и соответственно – утолщаться при сжатии. Если разделить поперечное укорочение-удлинение образца упругого вещества В, L на первоначальный размер образца в этом же направлении В, L (рис. 2.7), получим константу

v = В / В или v = L / L, (2.13)

которая называется коэффициент Пуассона – по имени французского ученого С.Д. Пуассона (S.D. Poisson, 1781–1840).

Модуль E и коэффициент v вместе образуют пару величин, которые полностьюхарактеризуютупругиесвойствалюбогоизотропноговещества – вещества,свойствакоторогоодинаковывовсехнаправлениях.

В случае, когда рассматривается сложное напряженное состояние, закон Гука записывается через компоненты нормальных (осевых) напряжений и деформаций в виде обобщенного закона (и тоже Гука):

64

или, что то же, через первые инварианты тензоров напряжений и деформаций:

Касательные же напряжения σij записываются через деформации εij так:

а через вторые инварианты тензора напряжений и деформаций так:

Величина G называется модулем сдвига и выражается через E и v формулой

Существуют и многие другие формы записи обобщенного закона Гука и соответственно разные формы обозначения упругих параметров (констант): E и ν, G и ν, K и G, λ и μ. Последняя пара упругих констант называется постоянными Лямé (G.L.J.B. Lamé, 1795–1870, работал в России с 1820 по 1832 г.), а запись через них закона Гука следующая:

Независимо от формы представления этих констант, в каждом случае их только две, причем они, как показано в табл. 2.1, могут быть выражены одни через другие, в том числе через принятые здесь параметры Е и ν.

Самая компактная из записей закона Гука, выраженная через первый инвариант тензора напряжений Iσ = σ11 + σ22 + σ33 и так называемый символ Кронекера δij (который может принимать только два значения: δij = 1 при i = j и δij = 0 при i ≠ j), следующая:

65

Таблица 2.1

Соотношения между различными упругими постоянными (М.Н. Гольдштейн [2])

Например, чтобы выразить относительную осевую деформацию ε22 в направлении 2–2 (при этом δij = 1), путем подстановки получим

а чтобы выразить деформацию сдвига σ12 (при этом δij = 0), получим

Следует отметить еще одну форму записи закона Гука для анизотропной среды, у которой характеристики деформируемости различаются в разных направлениях или в разных точках. В общем случае анизотропными являются многие композиционные материалы типа стеклопластика. Но само понятие «упругость» для них оказывается значительно более сложным.

Задачи об учете различной деформируемости тел в разных направлениях служат предметом обсуждения новой ветви теории упругости –

разномодульной теории упругости (С.А. Амбарцумян, 1982 [4]).

В расчетах грунтов встречается случай, когда на одном из этапов нагружения в грунтовой среде в одном или нескольких направлениях происходит сжатие с характеристиками Е и ν, в другом с характеристиками, например, при растяжении – Е+ и ν+, при разгрузке – Е– и ν–.

Целесообразность применения к грунтам этой теории обусловлена тем, что различие модуле деформации при нагружении Е и растяжении Е+, а также при сжатии Е и разгрузке Е– различаются до 2–5, иногда до 10 раз.

66

Заметим, что различие в деформационных характеристиках большинства композиционных материалов редко превышает 2-кратной величины.

Физические соотношения в общем случае выражаются так:

где аij – коэффициенты, которые принимают значения 1/Е, 1/Е+ или 1/Е–; ν/Е, ν+/Е+ или ν–/Е– в зависимости от того, какой процесс – сжатие, растяжение или разгрузка – происходит на конкретном этапе нагружения.

Из энергетических соображений следует, что коэффициенты аij должны быть равны по обе стороны от главной диагонали. Это означает, что для практического использования в грунтах решений разномодульной теории упругости требуется определение характеристик сжимаемости – сжатия – растяжения Е, Е+ и Е–, что практически невозможно. Способов определения коэффициентов поперечной деформации применительно к различным случаям взаимного влияния напряжений разного знака – ν, ν+ и ν– на сегодня не существует.

Поэтому в практических расчетах принимают постоянный коэффициент Пуассона ν = ν+ = ν–, что однако встречает возражения специалистов в области классической теории упругости.

Тем не менее такой подход можно рассматривать как инженерный прием, позволяющий отразить принципиальное и значительное различие в работе грунта при разных знаках дополнительных напряжений, возникающих на определенном этапе нагружения грунтового массива (относительно напряжений, достигнутых на предыдущем этапе).

4 Распределение напряжений в массиве грунта

4.1 Общие представления о распределении напряжений в грунтах

Представление о том, как распределяются напряжения в массиве грунта, можно получить из рис. 2.8, на котором показаны лежащие вдоль оси Х одинаковые трубы или бревна правильной круговой формы, к которым вверху приложена некоторая сила, условно обозначенная как Р = 1. Разумеется, трубы или бревна моделируют грунтовые частицы, а картинка в целом – как весь грунтовый массив. В рассматриваемом случае верхний элемент массива (труба, бревно), к которому приложена сила Р = 1, передает двум нижним элементам второго сверху ряда по половине силы (Р/2), третьего ряда – по половине от сил второго ряда, в результате чего появляется неравномерность распределения сил: на

67

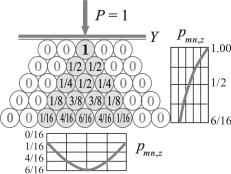
крайние элементы – по Р/4, на центральный – 2 Р/4 = Р/2, поскольку он воспринимает по половине сил от двух элементов 2-го ряда. И так далее, вплоть до бесконечности по глубине.

Можно легко вывести формулу для вычисления сил на каждый их элементов массива, имеющий порядковый номер ряда n и порядковый номер элемента в ряду m, начиная от центра. Однако такая формула не будет иметь практического

значения. Здесь важно отметить, что эти силы подчиняются закону равновесия в каждом ряду; например, в пятом ряду (n = 5): m1 + 2m2 + + 2m3 = 6/16 + 2 · 4/16 + 2 · 1/16 = 16/16 = 1.

Отсутствие практического интереса к подобным формулам объясняется тем, что здесь рассматривается идеализированный случай, когда все элементы массива однотипны, между элементами отсутствует трение и какая-либо связь, препятствующая передаче нагрузки вниз. Кроме того, на рис. 2.8 показан пример идеально плотной упаковки элементов, когда более плотной упаковки просто не существует. В случае же, если размеры элементов меняются, а упаковка менее плотная, ситуация каждый раз меняется.

Кроме того, и это очень важно, рис. 2.8 иллюстрирует плоскую задачу, когда элементы массива простираются бесконечно вдоль оси Х, перпендикулярной плоскости чертежа. Если вместо труб принять шары (или квадратные в плане блоки, кирпичи), передача сил от ряда к ряду уже будет идти по другому закону, поскольку верхний шар будет передавать силу не двум, а трем-четырем нижним шарам (в зависимости от плотности упаковки). Легко показать, что в случае шаров иллюстрируется подобие пространственной задачи, когда действие силы будет распространяться на меньшее расстояние по глубине (координаты Z), а сила будет убывать от ряда к ряду против плоского случая, хотя в обоих случаях действие ее распространяется до бесконечной глубины.

Грунтовые частицы можно уподобить шарам, трубам или кирпичам, но, как правило, разного размера, вплоть до микроскопического. Они могут быть как связаны, так и не связаны с соседними частицами, но общая тенденция к уменьшению сил с глубиной будет сохраняться, причем по-разному в плоском и в пространственном случаях.

В целом нужно отметить, что существует целое научное направление в механике (см. И.И. Кандауров, 1966 [5] и др.), которое занимается

68

вопросами распределения напряжений в дискретных средах, какими являются любые раздробленные вещества – зерно, мука, руда, шлаки, а в частном случае – грунты.

При переходе к бесконечно малым размерам частиц пользуются уже не силами, а напряжениями – теми же силами, но распределенными по некоторой площадке, размер которой может быть разным – от бесконечно малого (как в теории упругости) до конечного. Считается, что размер площадки, на которой будет анализироваться распределение сил, должен быть в 20–30 раз больше размера частиц. Это реально, поскольку площадки, по которым распределяются силы, обычно принимаются равными по площади 1 см2 или 1 м2, т.е. существенно превосходящими размеры большинства грунтовых частиц.

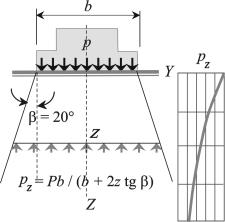
Взаключение пояснения распределения сил и напряжений в массиве на рис. 2.9 приводится еще один пример распределения напряжений в плоской задаче, в которой напряжения в сплошной (не дискретной) среде принимаются распределенными под «углом видимости» β; обычно принимается

β= 20…30°.

Вобщем случае распределение напряжений на некоторой глу-

болическому, треугольному, по кривой нормального распределения случайных величин К.Ф. Гаусса

(J.C.F. Gauß, 1777–1855) и др. Для равномерного распределения формула для напряжений приведена на рис. 2.9. Очевидно, что для пространственного случая – прямоугольного фундамента со сторонами l (длина) и b (ширина), нагруженного равномерно распределенной нагрузкой р, формула для рz имеет вид

В табл. 2.2 приведено сравнение расчетов вертикальных напряжений при угле видимости β, равном 20° и 30° для фундамента со сторонами l b = 2.8 2.0 м (пространственная задача) и для ленты шириной b = 2.0 м (плоская задача) при давлении по подошве р = 20 тс/м2.

69

В дальнейшем будет показано, как та же задача решается методами теории упругости (соответствующие значения σz приведены в двух последних столбцах таблицы).

Как видно из табл. 2.2, различия в расчетах между решениями не очень значительны, что вполне объяснимо упрощенной схемой «угла видимости».

Примеры иллюстрируют различие плоской и пространственной задач: при «углах видимости» β = 20…30°, как и по теории упругости, в пространственной задаче напряжения на глубине 4 м примерно в 2 раза меньше, чем в плоской.

Несмотря на очевидную условность схемы с «углами видимости», эти формулы до сих пор используются для приблизительной оценки распределения напряжений по глубине.

4.2 Как решается задача о распределении напряжений методами теории упругости

Выше уже говорилось о том, что в расчетах фундаментов специалисты постепенно начиная с конца ХIХ в. стали подходить к использованию задач о распределении напряжений в сплошных средах, которые до этого ранее решались примерно 300 лет многими учеными, начиная с Г. Галилея, а, скорее всего, много раньше. Знания в этой области со временем оформились в самостоятельную науку – теорию упругости и входят в состав наук еще более высокого уровня. А знания из теории упругости (с корректировками на учет существенных особенностей происхождения и свойств грунтов) «перетекали» в постепенно формирующуюся с 1920–30-х гг. самостоятельную науку об основаниях и фундаментах и ее теоретического раздела – механики грунтов.

Началом классической механики грунтов можно считать 1885 г., когда была опубликована работа французского академика Ж.В. Бусси-

70