Тема 8

Отражение и преломление плоских волн.

1 . Поле однородной плоской волны, распространяющемся в произвольном направлении.

При решении многих практически важных задач нельзя считать, что среда является однородной. На структуру поля и характер распространения волны существенно влияет граница раздела сред, обладающих разными свойствами. Попадая на поверхность раздела двух сред, электромагнитная волна может частично (или полностью) отразиться либо частично (либо полностью) пройти в другую среду. Кроме того, возможно и более сложное явление, называемое дифракцией волн.

Рассматриваем задачу такого типа: падение плоской электромагнитной волны на плоскую бесконечно протяженную границу раздела двух однородных изотропных сред. При анализе распространения плоской электромагнитной волны в неограниченной однородной среде использована прямоугольная система координат, одна из осей которой (ось ) совпадала с направлением распространения волны.

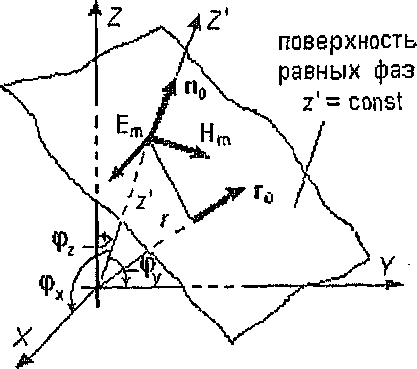Рассмотрим линейно поляризованную волну. Предположим, что волна распространяется в однородной изотропной среде вдоль оси , образующей с осями прямоугольной системы координат углы соответственно (рис.23). Поле однородной плоской волны в среде без потерь можно представить в виде

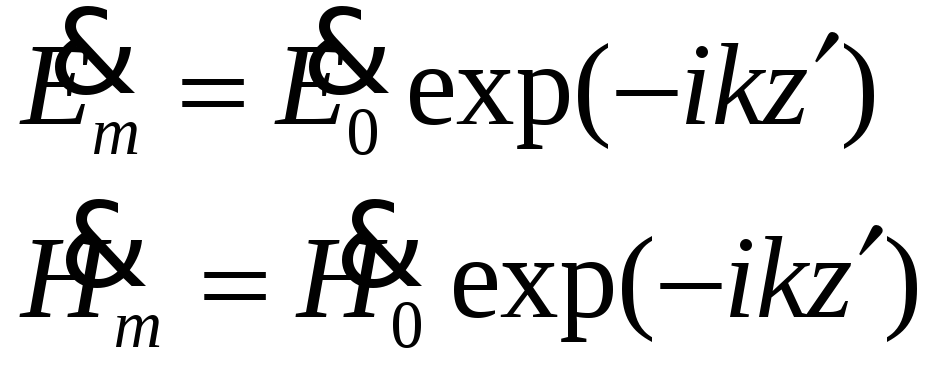(1)

где - переменная, определяющая положение точки на оси .

Векторы и не зависят от координат и лежат в плоскостях, перпендикулярных оси , причем

(2)

где - координатный орт переменной . Поверхности равных фаз волны (1) образуют семейство плоскостей, перпендикулярных оси Z', и удовлетворяют уравнению , где - радиус-вектор, проведенный из начала координат до произвольной точки, лежащей на рассматриваемой ПРФ. Для перехода к координатам нужно вычислить скалярное произведение вектора на вектор . Учитывая, что , запишем

(3)

П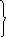одставляя выражение (3) в (1), получаем

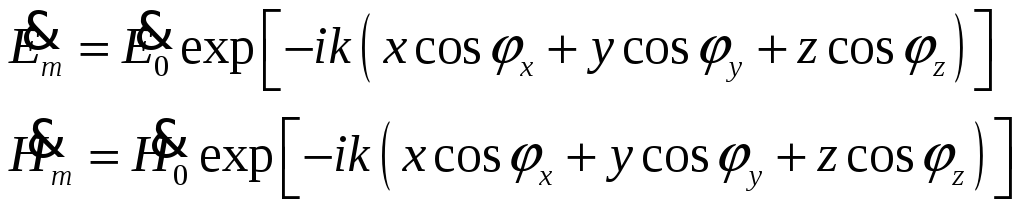(4)

Если проводимость среды отлична от нуля, то в формуле (4) нужно параметр считать комплексной величиной, равной , векторы и - значениями комплексных амплитуд векторов в начале координат, a в соотношении (2) заменить на .

Прежде чем перейти к анализу волновых явлений на границе раздела двух сред, введем некоторые определения. Назовем плоскость, проходящую через нормаль к поверхности раздела двух сред параллельно направлению распространения волны, плоскостью падения. Вектор напряженности электрического поля плоской волны перпендикулярен направлению ее распространения, а по отношению к плоскости падения может быть ориентирован произвольно. Однако, не нарушая общности анализа, можно ограничиться рассмотрением двух ориентаций вектора , а именно:

вектор перпендикулярен плоскости падения (нормально поляризованная плоская волна);

вектор параллелен плоскости падения (параллельно поляризованная плоская волна).

Очевидно, что волну с любой другой ориентацией вектора , а также волны, имеющие круговую или эллиптическую поляризацию, можно представить в виде суперпозиции двух волн, одна из которых является нормально поляризованной, а вторая - параллельно поляризованной.

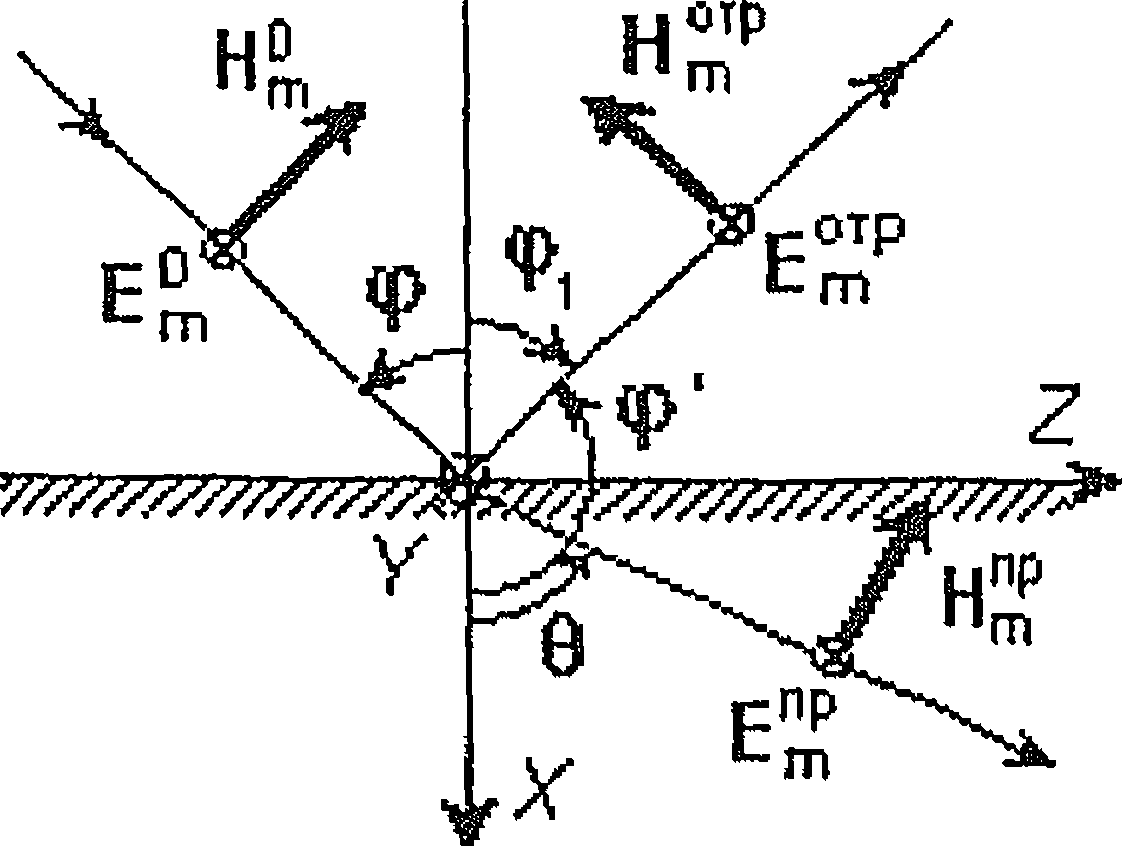
2. Падение нормальной поляризованной плоской волны на границу раздела двух сред.

Пусть линейно поляризованная плоская электромагнитная волна падает на плоскую бесконечно протяженную границу раздела двух однородных изотропных сред, характеризуемых параметрами соответственно. Введем прямоугольную систему координат так, чтобы плоскость совпадала с поверхностью раздела, а плоскость падения-с плоскостью . Угол между направлением распространения волны и нормалью к поверхности раздела будем называть углом падения (рис. 24).

В выбранной системе координат направляющие косинусы, определяющие направление распространения волны,

(5)

Следовательно, фазовый множитель падающей волны имеет вид

Предполагается, что падающая волна является нормально поляризованной. В этом случае соответствующий ей вектор напряженности электрического поля параллелен оси . При этом вектор напряженности магнитного поля лежит в плоскости падения (рис.25). Подставляя формулы (5) в (4) и учитывая, что в рассматриваемом случае - характеристическое сопротивление волны в первой среде, получаем

Рис.24

Рис.25

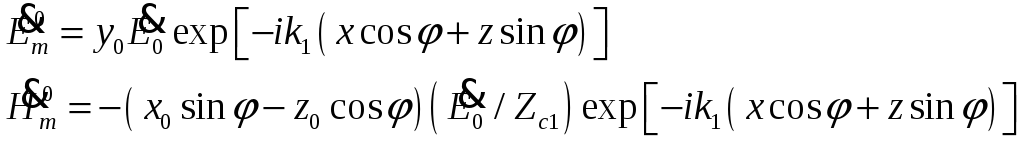(6)

где .

Отметим, что постоянная равна значению комплексной амплитуды - й составляющей напряженности электрического поля в начале координат (при ). Соответственно векторная постоянная равна значению комплексной амплитуды вектора в начале координат.

Из физических соображений очевидно, что падающая волна может частично (или полностью) отразиться от границы раздела () и частично (или полностью) пройти во вторую среду. Естественно предположить, что отраженная и преломленная волны будут плоскими.

Если, исходя из этого предположения, удастся найти поле, удовлетворяющее граничным условиям

(7)

где - касательные составляющие векторов в первой и во второй средах соответственно, то это поле будет решением рассматриваемой задачи.

Граничные условия (7) должны выполняться на всей плоскости , т.е. при любых значениях переменных . Так как поле падающей волны (6) не зависит от переменной , то необходимо предположить, что поле отраженной и преломленной волн также не зависит от координаты . Это означает, что векторы, определяющие направление распространения отраженной и преломленной волн, параллельны плоскости . Можно также предположить, что отраженная и преломленная волны являются нормально поляризованными (рис.25). С учетом сделанных предположений выражения для векторов поля отраженной волны могут быть получены из формул (6), если в последних заменить , , где - угол между осью и направлением распространения отраженной волны (см. рис.24 и 25), а - некоторая, пока неизвестная постоянная, равная значению комплексной амплитуды -й составляющей напряженности электрического поля отраженной волны. Обычно вместо угла рассматривают угол , называемый углом отражения. Так как , то . При этом

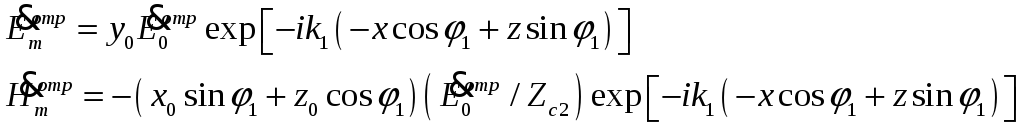
(8)

где .

Поле преломленной волны определяется аналогично:

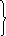(9)

где ; ; - угол преломления (рис.7.3); - характеристическое сопротивление волны во второй среде, a - некоторая, постоянная, равная значению комплексной амплитуды -й составляющей напряженности электрического поля преломленной волны. Ориентация векторов и падающей, отраженной и преломленной волн показана на рис.25. Углы и так же, как и постоянные и подлежат определению.

Граничные условия (7) должны выполняться при всех значениях координаты . Это возможно только в том случае, если зависимость векторов и от переменной во всех трех волнах будет одинаковой. Поэтому необходимо, чтобы

(10)

(11)

Так как углы и заключены в интервале , то из равенства (10) следует первый закон Снеллиуса , ("Угол падения равен углу отражения"). Из равенства (11) вытекает соотношение , которое в случае идеальных однородных изотропных сред выражает второй закон Снеллиуса ("Отношение синуса угла преломления к синусу угла падения равно относительному показателю преломления сред "). Действительно, коэффициент преломления среды , где - скорость света в вакууме, а - скорость света (фазовая скорость волны ) в рассматриваемой среде). Следовательно, , где и - фазовые скорости волны в первой и второй средах соответственно.

Отметим, что соотношение (11) остается верным и в случае проводящих сред. Пусть, например, первая среда - идеальный диэлектрик, а вторая обладает проводимостью, отличной от нуля. Тогда параметр будет комплексной величиной, а , и угол останутся вещественными. Для выполнения равенства (11) при этом придется считать величину комплексной, не имеющей простого геометрического смысла (см. 6).

Для определения постоянных используем граничные условия (7). Так как поле в первой среде складывается из полей падающей и отраженной волн, а поле во второй среде совпадает с полем преломленной волны, то формулы (7) принимают вид

(12)

Подставляя в эти выражения значения соответствующих составляющих комплексных амплитуд напряженности электрического и магнитного полей и учитывая равенства (10) и (11), приходим к соотношениям

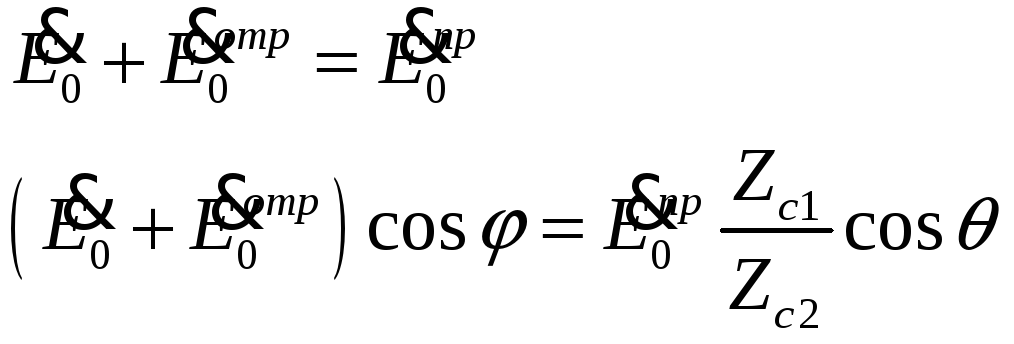(13)

Как видно, постоянные и пропорциональны :

(14)

где и - коэффициенты отражения и прохождения соответственно. Их также часто называют коэффициентами Френеля. Символ означает, что рассматриваются нормально поляризованные волны. Деля обе части уравнений (13) на , получаем

(15)

Решая эту систему уравнений, находим значения коэффициентов Френеля для случая нормальной поляризации:

(16)

(17)

В формулах (15) и (16) можно исключить угол преломления , выразив через синус угла падения . Указанные формулы справедливы и в том случае, если одна из сред (или обе среды) обладают проводимостью. При этом диэлектрическая проницаемость соответствующей среды будет комплексной величиной, комплексными также будут соответствующие параметры и , а следовательно, и коэффициенты и .

Как видно из формул (14), модуль коэффициента отражения представляет собой отношение амплитуд напряженностей электрических полей отраженной и падающей волн в точке отражения (в рассматриваемом случае в любой точке границы раздела сред), а его аргумент равен разности фаз этих напряженностей в той же точке. Аналогично определяются модуль и аргумент коэффициента прохождения: в этом случае нужно только вместо отраженной волны рассматривать преломленную волну.

В тех случаях, когда проводимостью обладает только вторая среда, а магнитные проницаемости обеих сред одинаковы, формулу (16) обычно записывают в несколько иной форме. Пусть, например, первая среда - воздух ), тогда выражение (16) может быть переписано в виде

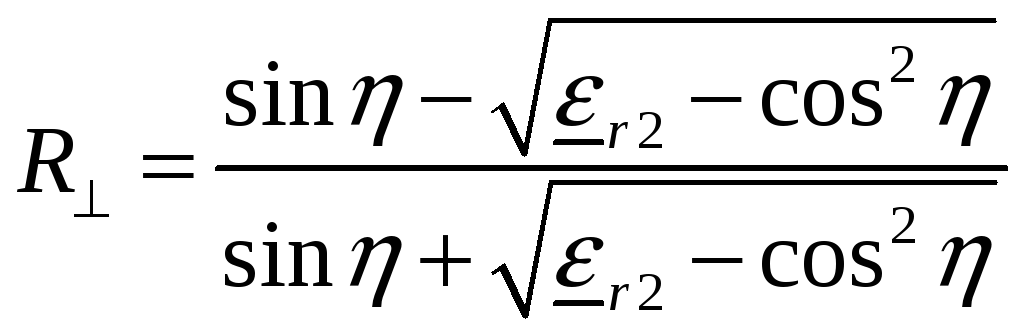
где - угол между направлением распространения падающей волны и плоскостью раздела; - комплексная относительная диэлектрическая проницаемость второй среды.

Для расчета электромагнитного поля, возникающего в результате падения на плоскую границу раздела двух сред нормально поляризованной плоской волны в первой среде, достаточно сложить поля, определямые формулами (6) и (8). При этом в формулах (8) нужно заменить на и учесть соотношение . Во второй среде искомое поле совпадает с полем преломленной волны и может быть рассчитано по формулам (9), в которых нужно учесть равенство и второй закон Снеллиуса (11).