
- •Колебания. Волны. Оптика
- •1.Колебания
- •1.1.Гармонические колебания
- •1.1.1. Идеальный гармонический осциллятор. Уравнение идеального осциллятора и его решение. Амплитуда, частота и фаза колебаний
- •1.1.2. Свободные колебания систем с одной степенью свободы. Комплексная форма представления гармонических колебаний
- •1.1.3. Примеры колебательных движений различной физической природы
- •1.1.3.1. Колебания груза на пружине
- •Где – коэффициент жёсткости пружины, – координата положения равновесия, х – координата груза (материальной точки) в момент времени ,- смещение от положения равновесия.
- •1.1.3.2. Маятники
- •1.1.4. Сложение колебаний (биения, фигуры Лиссажу). Векторное описание сложения колебаний
- •1.1.5. Энергия колебаний
- •1.2. Ангармонический осциллятор
- •1.2.1. Линейность и принцип суперпозиции. Границы его применимости
- •1.2.2. Ангармонический осциллятор
- •1.3. Свободные затухающие колебания осциллятора с потерями
- •Она пропорциональна числу колебаний за время релаксации.
- •1.4. Вынужденные колебания. Время установления вынужденных колебаний. Его связь с добротностью осциллятора
- •1.5.Электромагнитные процессы в колебательном контуре с током
- •1.5.1. Свободные колебания в контуре
- •1.5.2. Свободные затухающие колебания в контуре
- •1.5.3. Вынужденные электрические колебания. Резонанс в последовательном контуре
- •1.5.4.Резонанс в параллельном контуре
- •1.5.5.Переменный ток
- •1.6.Связанные колебания. Нормальные моды связанных осцилляторов
- •1.6.1.Системы с двумя степенями свободы Нормальные моды колебаний
- •1.6.2.Общее решение для мод
- •2.Волны в упругой среде
- •2. 1. Волновое движение. Продольные и поперечные волны
- •2.2. Волновое уравнение в пространстве. Плоская гармоническая волна. Длина волны, волновое число, фазовая скорость. Одномерное волновое уравнение. Упругие волны в газах, жидкостях и твердых телах
- •2.3.Энергия волны
- •2.4.Принцип суперпозиции волн
- •2.5.Образование стоячих волн
- •2.6.Свободные колебания системы со многими степенями свободы. Волны – колебания непрерывных систем
- •2.7. Стоячие волны как нормальные моды колебаний
- •2.8. Моды поперечных колебаний непрерывной струны
- •2.9. Эффект Доплера
- •2.10. Электромагнитные волны
- •2.10.2. Энергетические характеристики электромагнитных волн. Вектор Пойнтинга
- •2.10. 2.1.Энергия и импульс электромагнитного поля. Сохранение энергии и импульса в изолированной системе произвольно движущихся зарядов
- •2.10.2.2. Работа, совершаемая полем при перемещении зарядов
- •2.10.2.3.Энергия электромагнитного поля. Плотность и поток энергии. Закон изменения энергии
- •2.10.2.4. Закон сохранения энергии для изолированной системы «поле- заряды»
- •2.10.2.5. Импульс электромагнитного поля. Закон сохранения импульса и момента импульса
- •2.10.3 Излучение диполя
1.5.4.Резонанс в параллельном контуре
Рассмотрим колебательный контур, в котором индуктивность L и ёмкостьСсоединены параллельно (рис.1.5.9).
Будем
считать активное сопротивление близким
к нулю, R≈0. Для амплитуд
напряжений на индуктивности и ёмкости
имеем:![]()
По
второму правилу Кирхгофа
![]() токи
токи![]() и
и![]() в каждый момент времени находятся в
противофазе, поэтому
в каждый момент времени находятся в
противофазе, поэтому![]()
Ток в неразветвлённой
цепи равен
![]() ,
или
,
или![]() .
.
При
1/ωL=ωCтокI=0. Условие резонанса
токов![]() –
частота колебаний равна собственной:
–
частота колебаний равна собственной:![]()
1.5.5.Переменный ток
Установившиеся вынужденные колебания можно рассматривать как протекание в цепи, обладающей ёмкостью, индуктивностью и активным сопротивлением, переменного тока, который обусловлен переменным напряжением:
![]() .
.
Ток
изменяется по закону
![]() амплитуда
тока
амплитуда
тока![]()
Ток
отстаёт от напряжения по фазе на угол
![]() :
:
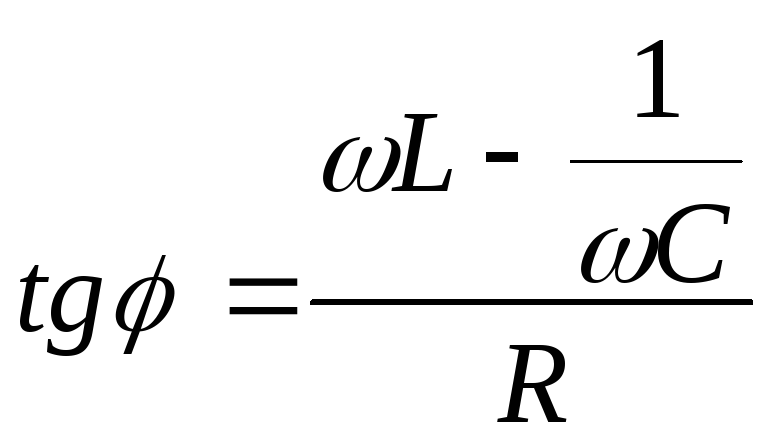 .Если
.Если
![]() <0,
ток опережает напряжение.
<0,
ток опережает напряжение.
Полное
электрическое сопротивление(импеданс)
равно
![]() ,
,
где
R- активное сопротивление,![]() -реактивное индуктивное сопротивление,
-реактивное индуктивное сопротивление,![]() - реактивное емкостное сопротивление.
- реактивное емкостное сопротивление.
Ток
на индуктивности отстаёт от напряжения
на π/2, а ток на емкости
опережает напряжение наπ/2.
Выражение![]() представляет собой реактивное
сопротивление или реактанс.
представляет собой реактивное
сопротивление или реактанс.
С
учётом сказанного
![]() Таким образом, если значения сопротивленийRиXотложить вдоль катетов треугольника,
то длина гипотенузы будет численно
равнаZ (рис.1.5.10).
Таким образом, если значения сопротивленийRиXотложить вдоль катетов треугольника,
то длина гипотенузы будет численно
равнаZ (рис.1.5.10).
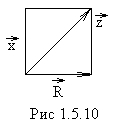 Мощность,
выделяемая в цепи переменного тока
равна
Мощность,
выделяемая в цепи переменного тока
равна![]()
Из
тригонометрии
![]() .
Тогда
.
Тогда![]() Среднее значение
Среднее значение![]() обозначимр. Среднее значение
обозначимр. Среднее значение![]() ,
тогда
,
тогда
![]()
 .
.
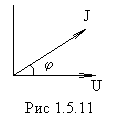
Однако
![]() тогда
тогда![]() (рис.1.5.11).
(рис.1.5.11).
Такую
же мощность развивает постоянный ток
силой
![]() Это значение силы тока называется
эффективным или действующим.
Это значение силы тока называется
эффективным или действующим.
Аналогично
![]() действующее значение напряжения.
действующее значение напряжения.
Тогда средняя
мощность
![]() ;
величина
;
величина![]() называется коэффициентом мощности. Чем
меньше
называется коэффициентом мощности. Чем
меньше![]() ,тем ближе
,тем ближе![]() к 1, тем больше мощность.
к 1, тем больше мощность.
Лекция 5
1.6.Связанные колебания. Нормальные моды связанных осцилляторов
1.6.1.Системы с двумя степенями свободы Нормальные моды колебаний
Особый интерес представляет случай, когда одна колеблющаяся система связана с другой системой, которая тоже может колебаться. В этом случае для каждого из осцилляторов можно записать свое уравнение динамики, эти уравнения в общем случае не являются независимыми. Каждый осциллятор имеет свою частоту, амплитуду и фазу, т.е. система обладает двумя степенями свободы.
 Такие
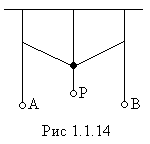
системы называются связанными. Простой
пример связи – два маятника, соединённые
нитью, к середине которой подвешен грузР (рис.1.1.14). При помощи
силы, действующей на нить, маятник А
связан с маятником В.
Если маятник В во время
колебания удалится от А,
то сила связи между этими маятниками
становится больше, а при сближении –
меньше. Маятник А получает
в такт с колебаниями маятника В
импульс периодически действующей силы,
частота которой согласуется с частотой
собственных колебаний А,
но может отличаться от частоты колебаний
В.
Такие
системы называются связанными. Простой
пример связи – два маятника, соединённые
нитью, к середине которой подвешен грузР (рис.1.1.14). При помощи
силы, действующей на нить, маятник А
связан с маятником В.
Если маятник В во время
колебания удалится от А,
то сила связи между этими маятниками
становится больше, а при сближении –
меньше. Маятник А получает
в такт с колебаниями маятника В
импульс периодически действующей силы,
частота которой согласуется с частотой
собственных колебаний А,
но может отличаться от частоты колебаний
В.
Под влиянием силы связи между маятниками разной длины маятник А приходит в колебательное движение. Когда маятник В колеблется, его амплитуда возрастает с каждым новым импульсом, в то время, как амплитуда В убывает. Спустя известное время, амплитуды маятника А убывают, а маятника В возрастают до тех пор, пока не наступит обратное явление. Таком образом, энергия колебаний передаётся через связь от одной колеблющейся системы другой и обратно.
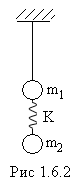 Если
периоды собственных колебаний обоих
маятников равны, то обмен энергией
осуществляется нацело.
Если
периоды собственных колебаний обоих
маятников равны, то обмен энергией
осуществляется нацело.
Из эксперимента известно, что процесс передачи энергии между маятниками идёт тем быстрее, чем больше масса груза Р. Если два маятника колеблются с одинаковыми периодами, амплитудами и фазами колебаний, то никакого обмена энергией между ними не происходит. Должна быть разница в амплитудах или фазах колебаний, чтобы энергия была получена или отдана.
В природе есть много интересных систем, имеющих две степени свободы. Например, двойной маятник – один маятник подвешен к опоре, другой - к гире первого маятника (рис.1.6.1); два маятника, связанные пружиной (рис.1.6.2, 1.6.3); горизонтальная нить с двумя шариками (рис.1.6.4).
В общем случае движение системы с двумя степенями свободы может иметь очень сложный вид, не похожий на простое гармоническое движение.
Можно
показать, что для двух степеней свободы
и при линейных уравнениях движения
наиболее общее движение является
суперпозицией двух независимых простых
гармонических движений, происходящих
одновременно. Эти два простых гармонических
движения называются нормальными или
собственными колебаниями или г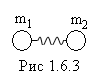 армониками,
а так же нормальными модами колебаний
или просто модами. Создавая определённые
начальные условия (определённые начальные
значенияxa,
xb
и dxa/dt,
dxb/dt)
можно создать систему, колебания которой
соответствуют только одной из мод.
армониками,
а так же нормальными модами колебаний
или просто модами. Создавая определённые
начальные условия (определённые начальные
значенияxa,
xb
и dxa/dt,
dxb/dt)
можно создать систему, колебания которой
соответствуют только одной из мод.
Нормальные колебания (нормальные моды) – это собственные (свободные) гармонические колебания линейных динамических систем с постоянными параметрами, в которых отсутствуют как потери, так и приток извне колебательной энергии. Каждое нормальное колебание характеризуется определенным значением частоты, с которой осциллируют все элементы системы, и формой — распределением амплитуд и фаз по элементам системы. Линейно независимые нормальные колебания, отличающиеся формой, но имеющие одну и ту же частоту, называются вырожденными. Частоты нормальных колебаний называются собственными частотами системы.
В дискретных системах, состоящих из N связанных гармонических осцилляторов (например, механических маятников, колебательных контуров), число нормальных колебаний равноN. В распределённых системах (струна, мембрана, резонатор) существует бесконечное, но счётное множество нормальных колебаний. Произвольное свободное движение колебательной системы может быть представлено в виде суперпозиции нормальных колебаний. При этом полная энергия движения распадается на сумму парциальных энергий, отдельных нормальных колебаний. Таким образом, линейная система ведёт себя, как набор независимых гармонических осцилляторов, которые могут быть выбраны в качестве обобщённых нормальных координат, описывающих движение в целом. Однако в динамических системах могут существовать и собственные движения, не сводящиеся к нормальным колебаниям (равномерные вращения, постоянные токи и др.).
При внешнем возбуждении системы нормальные колебания в значительной мере определяют её резонансные свойства. Резонанс может возникнуть лишь в том случае, когда частота гармонического внешнего воздействия близка к одной из собственных частот системы либо к их линейной комбинации, если внешнее воздействие меняет параметры системы (параметрический резонанс). При этом важным оказывается также и пространственное распределение воздействия — максимальный эффект достигается при соблюдении не только временного, но и «пространственного синхронизма».
В линейных системах с переменными параметрами при выполнении определенных условий также возможно представление движений в виде суперпозиции нормальных колебаний, отличающихся, однако, от гармонических. Понятие нормальных колебаний может быть приближённо распространено на системы, содержащие неконсервативные и нелинейные элементы, если их воздействие приводит к медленным изменениям амплитуд и фаз квазигармонических нормальных колебаний (в масштабе периода самих нормальных колебаний или периода биений между ними).
С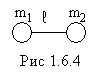 войства
мод. Если
существует лишь одна мода колебаний,
то в системе совершается простое
гармоническое движение. Все части
системы колеблются с одной частотой,
одновременно проходя через положение
равновесия (для которого х=0).
Например, движения
войства
мод. Если
существует лишь одна мода колебаний,
то в системе совершается простое
гармоническое движение. Все части
системы колеблются с одной частотой,
одновременно проходя через положение
равновесия (для которого х=0).
Например, движения
![]() или
или
![]() не могут соответствовать одной моде,
так как в первом случае различны фазовые
постоянные, во втором – частоты.
не могут соответствовать одной моде,
так как в первом случае различны фазовые
постоянные, во втором – частоты.
Рассмотрим моду, движение которой описывается уравнением
![]() .
(1.6.1)
.
(1.6.1)
назовем ее мода 1. Из уравнения движения видно, что у обеих степеней свободы одна и та же частота и фаза. Для моды 2 получаем
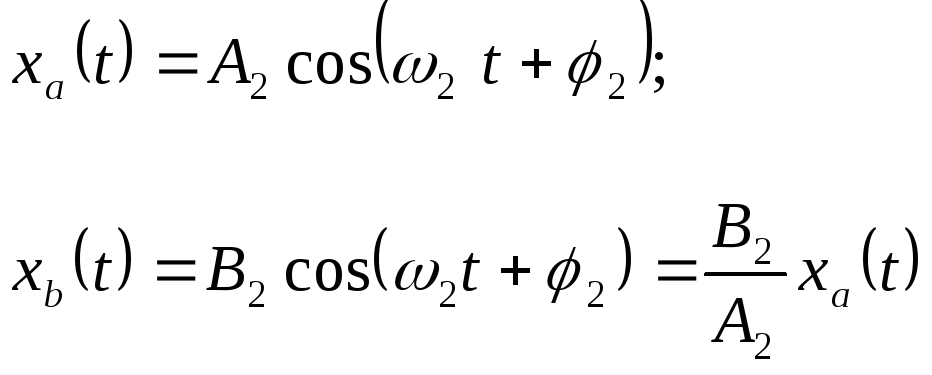
 .
(1.6.2)
.
(1.6.2)
Каждая
мода имеет свою собственную частоту:
![]() для моды 1
и
для моды 1
и
![]() для моды
2.
для моды
2.
Для
каждой моды система имеет характерную
“конфигурацию” или “форму”, определяемую
отношением амплитуд движений по двум
направлениям:
![]() для моды 1
и
для моды 1
и
![]() для
моды 2. Для данной моды отношениеxa/xb
постоянно и не зависит от времени, оно
определяется в нашем случае отношением
для
моды 2. Для данной моды отношениеxa/xb
постоянно и не зависит от времени, оно
определяется в нашем случае отношением
![]() или
или![]() ,
которые могут быть либо положительными,
либо отрицательными.
,
которые могут быть либо положительными,
либо отрицательными.
Наиболее общим движением является суперпозиция, при которой движение содержит обе моды колебаний одновременно:
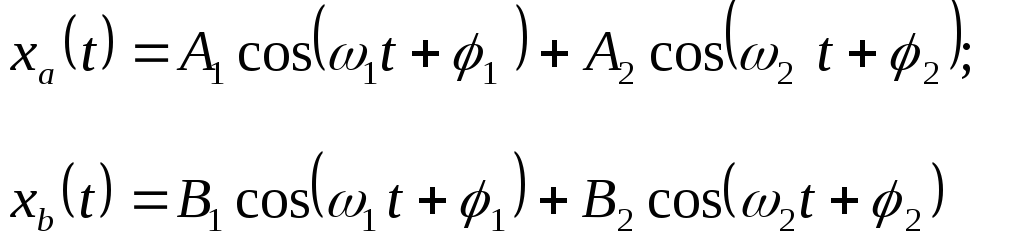 .
(1.6.3)
.
(1.6.3)
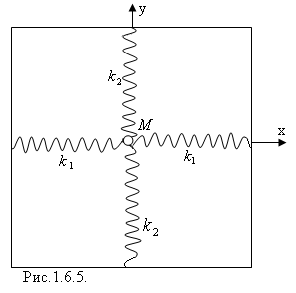
В
качестве примера рассмотрим двумерный
гармонический осциллятор (рис.1.6.5). Масса
М,
укреплённая на двух парах взаимно
перпендикулярных пружин, может свободно
двигаться в плоскости ХУ.
В направлении оси Х
она соединена со стенками двумя невесомыми
пружинами с коэффициентами жёсткости
![]() ,
а в направленииУ
– двумя другими невесомыми пружинами
с коэффициентом жёсткости
,
а в направленииУ
– двумя другими невесомыми пружинами
с коэффициентом жёсткости
![]() .
В случае малых колебанийx-компонента
возвращающей силы полностью обусловлена
пружинами
.
В случае малых колебанийx-компонента
возвращающей силы полностью обусловлена
пружинами
![]() ,
ау-составляющая
возвращающей силы зависит только от
пружин
,
ау-составляющая
возвращающей силы зависит только от
пружин
![]() .
В положении равновесия система имеет
вид, представленный на рис.1.6.5. Сообщим
массеМ
небольшое смещение х
в направлении +х,
тогда возвращающая сила станет равна
.
В положении равновесия система имеет
вид, представленный на рис.1.6.5. Сообщим
массеМ
небольшое смещение х
в направлении +х,
тогда возвращающая сила станет равна
![]()
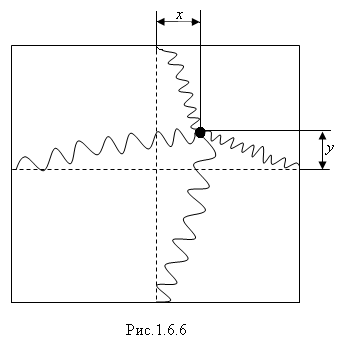
Теперь
из этого положения дадим массе небольшое
смещение у
в направлении +у.
Нужно выяснить, изменилось ли значение
![]() .
.
Пружины
![]() изменили длину на малую величину,
пропорциональную
изменили длину на малую величину,
пропорциональную![]() .
Этим изменением мы пренебрегаем ввиду
малости
.
Этим изменением мы пренебрегаем ввиду
малости![]() .
Пружины
.
Пружины![]() изменили длину на величину, пропорциональнуюу
(одна стала короче, другая - длиннее), но
проекции соответствующих им сил на
направление Х
так же пропорциональны х.
При этом х–составляющая
силы от пружины
изменили длину на величину, пропорциональнуюу
(одна стала короче, другая - длиннее), но
проекции соответствующих им сил на
направление Х
так же пропорциональны х.
При этом х–составляющая
силы от пружины
![]() пропорциональна произведению двух
малых величинху,
и этой составляющей мы также пренебрегаем.
пропорциональна произведению двух
малых величинху,
и этой составляющей мы также пренебрегаем.
Тогда
можно считать, что величина
![]() не изменилась, то же можно сказать и о
не изменилась, то же можно сказать и о
![]() .
Мы получили два линейных уравнения:
.
Мы получили два линейных уравнения:
![]() решения которых
решения которых
![]() (1.6.4)
(1.6.4)
 Из этих
уравнений следует, что движения в
направлениях Х
и У
не связаны между собой, и каждое движение
представляет собой гармоническое
колебание с собственной частотой.
Движение вдоль оси Х
соответствует одной нормальной моде
колебаний, а вдоль оси У
– другой моде. Колебания вдоль оси Х
(1 мода) имеют амплитуду
Из этих
уравнений следует, что движения в
направлениях Х
и У
не связаны между собой, и каждое движение
представляет собой гармоническое
колебание с собственной частотой.
Движение вдоль оси Х
соответствует одной нормальной моде
колебаний, а вдоль оси У
– другой моде. Колебания вдоль оси Х
(1 мода) имеют амплитуду
![]() и фазу
и фазу![]() ,
которая зависит только от начальных
условийх(0)
и х'(0),
то есть от смещения и скорости в момент
времени t=0.
Аналогично, для колебаний вдоль оси У
(2 мода) амплитуда
,
которая зависит только от начальных
условийх(0)
и х'(0),
то есть от смещения и скорости в момент
времени t=0.
Аналогично, для колебаний вдоль оси У
(2 мода) амплитуда
![]() и фаза
и фаза![]() зависят только от начальных значенийу(0)
и у'(0).
зависят только от начальных значенийу(0)
и у'(0).
х'![]() амплитуда
амплитуда![]() ,
а для
,
а для![]()
![]() =0.
Столь удачно выбранные нами координатых и у
называются нормальными координатами.
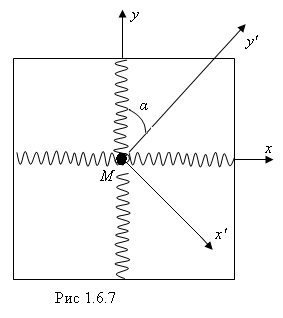
Рассмотрим систему координат х'у',
которая связана с ху
поворотом на угол α.
=0.
Столь удачно выбранные нами координатых и у
называются нормальными координатами.
Рассмотрим систему координат х'у',
которая связана с ху
поворотом на угол α.
Из рисунка 1.6.7 видно, что нормальная координата xпредставляет собой линейную комбинациюх' иу'; то же следует сказать и о другой нормальной координате -у. Если бы мы работали с координатамих', у' вместох, у,то должны были бы получить два «связанных» дифференциальных уравнения с переменнымих', у'в каждом уравнении.
В большинстве задач, содержащих системы с двумя степенями свободы, не так легко «на глаз» найти нормальные координаты. Как правило, уравнения движения для систем с двумя степенями свободы – это два связанных уравнения. Один из методов решения таких связанных дифференциальных уравнений – это поиск новых переменных, которые являлись бы линейной комбинацией первоначальных, неудачно выбранных координат и которые давали бы не связанные, а разделённые уравнения движения. Такие новые координаты называются нормальными.
В нашем примере для получения нормальных координат нам нужно повернуть оси х' иу'на уголαдо совпадения их с осямихиу.
