(1.1.1)

где х -смещение колеблющейся величины от положения равновесия,А –амплитуда колебаний, равная величине максимального смещения,-фаза колебаний, определяющая смещение в момент времени,-начальная фаза, определяющая величину смещенияв начальный момент времени,-циклическая частотаколебаний .

Период- время одного полного колебания, где- число колебаний, совершенных за время.

Частота колебаний-определяет число колебаний, совершаемых в единицу времени, она связана с циклической частотой соотношением, тогда период.

Циклическая частота– число колебаний за 2секунд.

Скоростьколеблющейся матер.

,

Ускорение

. (1.1.2)

Таким образом, скорость и ускорение гармонического осциллятора также изменяются по гармоническому закону с амплитудами исоответственно.

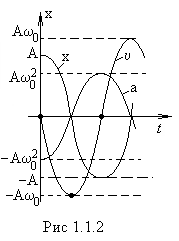При этом скорость опережает по фазе смещение на , а ускорение – на(рис.1.1.2).

Из сопоставления уравнений движения гармонического осциллятора (1.1.1) и (1.1.2) следует, что

, или .(1.1.3)

Это дифференциальное уравнение второго порядка называетсяуравнением гармонического осциллятора.

Его решение содержит две постоянные А и , которые определяются заданием начальных условий.

Каждое конкретное колебание характеризуется определенными значениями А и . Значения этих величин для данного колебания могут быть определены из начальных условий, т.е. по значениям отклонений х₀ и скорости₀в начальный момент времени.

.

Отсюда .

Если периодически повторяющийся процесс описывается уравнениями, не совпадающими с (1.1.1), он называется ангармоническим.

Система, совершающая ангармонические колебания, называется ангармоническим осциллятором.

3. Свободные колебания систем с одной степенью свободы

В природе очень распространены малые колебания, которые система совершает вблизи своего положения равновесия. Если система, выведенная из положения равновесия, предоставлена себе, то есть на неё не действуют внешние силы, то такая система будет совершать свободные незатухающие колебания. Рассмотрим систему с одной степенью свободы.

Устойчивому равновесию соответствует такое положение системы, в котором её потенциальная энергия имеет минимум (q– обобщённая координата системы).

Отклонение системы от положения равновесия приводит к возникновению силы , которая стремится вернуть систему обратно.

Значение обобщённой координаты, соответствующей положению равновесия, обозначим , тогда отклонение от положения равновесия

Будем отсчитывать потенциальную энергию от минимального значения . ПримемПолученную функциюразложим в ряд Маклорена и оставим первый член разложения, имеем:

,

где .

Тогда с учётом введённых обозначений:

, (1.1.4)

С учётом выражения (1.1.4) для силы, действующей на систему, получаем:

Согласно второму закону Ньютона, уравнение движения системы имеет вид: ,

тогда

, (1.1.5)

Выражений (1.1.5) совпадает с уравнением (1.1.3) свободных гармонических колебаний при условии, что

, (1.1.6)

и имеет два независимых решения: и,

так что общее решение:

, или ,

где

Из формулы (1.1.6) следует, что частота:

- определяетсятолько собственными свойствами механической системы

- и не зависитот амплитуды и от начальных условий движения.

Зависимость координаты колеблющейся системы от времени можно определить в виде вещественной части комплексного выражения

,

где A=Xe^-iα– комплексная амплитуда, её модуль совпадает с обычной амплитудой, а аргумент – с начальной фазой.